Théorème du minimax de von Neumann - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Énoncé du théorème - Histoire d'une découverte - Le modèle économique sous-jacent - Expériences - Comprendre la rationalité - Postérité du théorème - Démonstrations

Postérité du théorème

Dans le domaine des mathématiques pures, le théorème de von Neumann est le premier d'une longue série de théorèmes du minimax qui le généralisent dans de multiples directions. Il a sans doute aussi eu une influence significative sur l'évolution de la programmation linéaire.

Dans d'autres domaines scientifiques, le minimax a joué un rôle non négligeable en théorie statistique de la décision et sur la conception de systèmes de calcul distribués.

Pour le meilleur ou pour le pire, le théorème de von Neumann a peut-être eu aussi une postérité philosophique : il aurait inspiré la pensée de John Rawls, qui invoque explicitement la notion de maximin dans l'élaboration de sa théorie de la justice. Critiqué avec virulence pour l'usage immodéré qu'il aurait fait du concept, Rawls a toutefois tenu à préciser qu'il n'avait jamais fait l'erreur de proposer la recherche du maximin « comme principe général de délibération rationnelle, quels que puissent être les niveaux de risque et d'incertitude » (« as the general principle of rational decision in all cases of risk and uncertainty »).

Robert Aumann

On laissera le mot de la fin à Robert Aumann qui dresse un bilan argumenté de la postérité du théorème de von Neumann. Pour lui, l'omniprésence du théorème dans les présentations de la théorie des jeux antérieures à 1960 était peut-être un peu injuste (la modélisation des jeux à somme nulle n'est pas l'essentiel de la théorie) mais s'explique par la simplicité du résultat. Par un retour de balancier encore plus injuste, les théoriciens des jeux ont eu tendance dans les décennies qui ont suivi à minimiser l'importance du théorème. Avec le recul que donne le temps, on ne peut pourtant que reconnaître son importance : par sa postérité en dehors de la théorie des jeux d'abord, mais aussi en théorie des jeux où l'appareil conceptuel qui le sous-tend reste central, il fournit un modèle simple particulièrement adapté pour tester les concepts plus techniques. Sa preuve a certainement ouvert la voie à John Nash, pionnier de la théorie des jeux à somme non nulle. En conclusion, pour Aumann, le théorème de von Neumann « s'il n'est pas la pièce maîtresse de la théorie des jeux, en demeure une pierre angulaire cruciale » (« While not the centerpiece of game theory, it is a vital cornerstone »).

Démonstrations

La preuve originelle de von Neumann, publiée en 1928, était assez difficile à suivre et utilisait des arguments topologiques. Dans un second article, publié en 1937, von Neumann propose une preuve beaucoup plus lisible où l'utilisation de la topologie passe désormais par l'utilisation du théorème du point fixe de Brouwer. Un an plus tard, en 1938, le mathématicien Jean Ville publie une nouvelle preuve du théorème d'un esprit très différent puisqu'elle ne repose plus sur des résultats topologiques fins mais sur des arguments élémentaires de géométrie des convexes (hyperplan d'appui). Dans l'important ouvrage qu'il publie en 1944 avec Oskar Morgenstern (Theory of games and economic behavior), John von Neumann donne d'ailleurs une preuve adaptée de celle de Ville et non plus celle qui repose sur le théorème de Brouwer. En 1950, c'est Hermann Weyl qui fournit une nouvelle démonstration, également basée sur des arguments de convexité. Enfin, en 1967, Guillermo Owen apporte une nouvelle preuve très concise, en utilisant une construction par récurrence transfinie.

Le théorème du minimax peut aussi être démontré comme corollaire du théorème plus général de Nash qui assure l'existence d'équilibres pour les jeux non coopératifs, même à somme non nulle ; comme les premières preuves du théorème de von Neumann, la démonstration du théorème de Nash repose sur des arguments topologiques (on peut utiliser le théorème du point fixe de Brouwer mais aussi le théorème du point fixe de Kakutani et donc exploiter la convexité).

On peut aussi le déduire du théorème de dualité en programmation linéaire, comme les théorèmes de l'alternative parmi lesquels il se laisse ranger si on le reformule. Dans la mesure où le théorème de dualité peut être prouvé indépendamment de la théorie des inéquations linéaires, par des méthodes algorithmiques (méthode du simplexe), cette approche est différente de celles évoquées précédemment et a surtout l'intérêt d'être constructive : en appliquant un algorithme de programmation linéaire, on parvient à expliciter le minimax et un équilibre de Nash pour le jeu.

La valeur du maximin en termes de programmes linéaires est précisément la suivante, en utilisant les notations de l'article programmation linéaire :

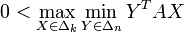
Proposition : Supposons $0<\max_{X\in\Delta_k}\min_{Y\in\Delta_n}Y^TAX$ .

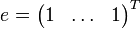
Alors, en notant $e=\begin{pmatrix}1&\ldots&1\end{pmatrix}^T$ , ce maximin est l'inverse de la valeur du programme linéaire :

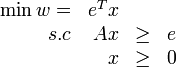
\begin{array}{rrll} \min w = & e^Tx & &\\ s.c & Ax &\geq& e\\ & x &\geq&0 \end{array}

Pour une exposition sommaire de certaines des démonstrations,

On signalera tout de même ici, ce qui est très facile à prouver, que l'une des inégalités du théorème se vérifie en deux lignes :

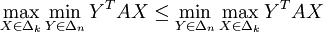
Remarque : Avec les notations du théorème de von Neumann, $\max_{X\in\Delta_k}\min_{Y\in\Delta_n}Y^TAX\leq\min_{Y\in\Delta_n}\max_{X\in\Delta_k}Y^TAX$ .

Elle a de fait déjà été utilisée dans la preuve de la proposition de la sous-section « Stratégies mixtes » et se vérifie exactement comme on vérifie l'inégalité analogue concernant les coefficients de la matrice A dans la preuve de la proposition de la sous-section « Points-selles dans les matrices de gain ».