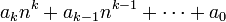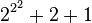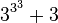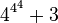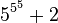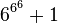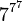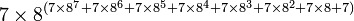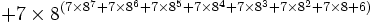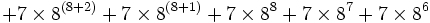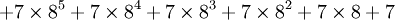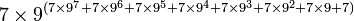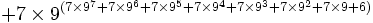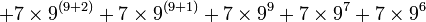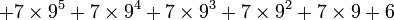Théorème de Goodstein - Définition
En logique mathématique, le théorème de Goodstein est un énoncé arithmétique qui est indécidable dans l'axiomatique des entiers naturels de Peano, mais peut être prouvé en utilisant l'axiomatique plus puissante de la théorie des ensembles, et plus particulièrement des ordinaux. Le théorème établit que toute suite de Goodstein se termine par 0. Il donne un exemple d'énoncé indécidable particulièrement simple, contrairement aux énoncés considérés dans le théorème d'incomplétude de Gödel.
Définition d'une suite de Goodstein
Avant de définir une suite de Goodstein, définissons d'abord la notation héréditaire en base n. Pour écrire un entier naturel dans une telle notation, on l'écrit d'abord sous la forme :
où chaque ai est un entier compris entre 0 et n-1. Ensuite, on applique le même traitement aux exposants k,k-1,... itérativement, jusqu'à obtenir une expression constituée uniquement d'entiers entre 0 et n-1.
Par exemple, 35 s'écrit en base 2 : 25 + 2 + 1 et en notation héréditaire en base 2 :
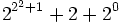
La suite de Goodstein d'un entier m, notée G(m), est définie comme suit : le premier élément de la suite est m. Pour obtenir l'élément suivant, on écrit m en notation héréditaire en base 2, puis on change chaque 2 en 3, et enfin on soustrait 1 du résultat. On a alors le deuxième élément de la suite. Pour obtenir le troisième, on écrit l'élément précédemment calculé en notation héréditaire en base 3, on change les 3 et 4, et on retranche 1. On continue ainsi jusqu'à obtenir 0.
Exemples de suites de Goodstein
Les premières suites de Goodstein se terminent rapidement. Par exemple G(3):
| Base | Notation héréditaire | Valeur | Notes |
|---|---|---|---|
| 2 | 21 + 1 | 3 | Le 1 represente 20. |
| 3 | 31 + 1 − 1 = 3 | 3 | On change 2 en 3, puis on soustrait 1 |
| 4 | 41 − 1 = 3 | 3 | On change 3 en 4 puis on soustrait 1 |
| 5 | 3 − 1 = 2 | 2 | Puisque la base utilisée est supérieure aux chiffres de la décomposition, les changements de base ultérieurs sont sans effet. |
| 6 | 2 − 1 = 1 | 1 | |
| 7 | 1 − 1 = 0 | 0 |
Les suites de Goodstein croissent en général pendant un grand nombre d'étapes. Par exemple, la suite G(4) commence comme suit :
| Notation héréditaire | Valeur |
|---|---|
| 22 | 4 |
| 2·32 + 2·3 + 2 | 26 |
| 2·42 + 2·4 + 1 | 41 |
| 2·52 + 2·5 | 60 |
| 2·62 + 6 + 5 | 83 |
| 2·72 + 7 + 4 | 109 |
| ... | |
| 2·112 + 11 | 253 |
| 2·122 + 11 | 299 |
| ... | |
| 2·232 | 1058 |
| 242+23·24+23 | 1151 |
| ... | |
La suite G(4) continue à croître.
Lorsqu'on atteint la base
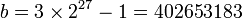
Lorsqu'on atteint la base
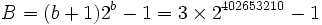
La suite se met enfin à décroître, et atteint la valeur nulle pour la base
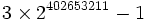
Cependant, l'exemple de G(4) ne donne pas encore une idée suffisante de la vitesse à laquelle la suite de Goodstein peut croître. G(19) croît beaucoup plus rapidement et commence comme suit :
| Notation héréditaire | Valeur |
|---|---|
|
|
19 |
|
|
7625597484990 |
|
|
environ 1.3 × 10154 |
|
|
environ 1.8 × 102184 |
|
|
environ 2.6 × 1036305 |
|
|
environ 3.8 × 10695974 |
|
|
environ 6 × 1015151335 |
|
|
environ 4.3 × 10369693099 |
| ... | |
En dépit de sa rapide croissance, le théorème de Goodstein établit que chaque suite de Goodstein se termine par un 0, quelle que soit la valeur initiale de m. A titre d'exemple, le nombre de termes de la suite G(5) se calcule comme suit. Posons :
-
- g(n) = n2n
-
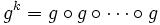
-
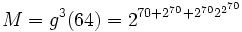
- N = gM(M),P = gN(N),Q = gP(P)
Le nombre de termes de la suite G(5) est alors Q-1.
Preuve
Le théorème de Goodstein peut être prouvé (en utilisant la théorie des ordinaux, plus puissante que les axiomes de Peano), comme suit : étant donnée une suite de Goodstein G(m), on construit une suite parallèle d'ordinaux dont les éléments ne sont pas plus petits que ceux de la suite donnée. Si cette suite parallèle se termine par 0, alors il en sera de même de la suite initiale.
Pour construire la suite parallèle, on prend la représentation héréditaire en base n, du (n-1)-ème élément de la suite de Goodstein, et on remplace chaque instance de n par le premier ordinal infini ω. Addition, multiplication et exponentiation de nombres ordinaux sont bien définis, et le résultat est un ordinal qui n'est pas plus petit que l'élément original de la suite de Goodstein.
Le changement de base de la suite de Goodstein ne modifie pas l'élément de la suite parallèle ; remplacer tous les 4 dans 4^(4^4) + 4 par ω est identique à remplacer tous les 4 par 5, puis remplacer les 5 par ω. L'opération de soustraction, cependant, revient à diminuer l'ordinal de la séquence parallèle. Par exemple, ω^(ω^ω) + ω décroît en ω^(ω^ω) + 4 si on est en base 5. Du fait que les ordinaux sont bien ordonnés, il n'existe pas de suite infinie strictement décroissante d'ordinaux. Aussi la suite parallèle doit-elle se terminer par 0 en un nombre fini d'étapes. La suite de Goodstein, majorée par la suite parallèle, devra faire de même.
Tandis que la preuve du théorème de Goodstein est relativement facile, le théorème de Kirby-Paris qui énonce que le théorème de Goodstein ne peut être prouvé à l'aide des seuls axiomes de Peano, est très technique et considérablement plus difficile. Il utilise des modèles non standard dénombrables de l'arithmétique de Peano
Bibliographie
- R. Goodstein, " On the restricted ordinal theorem ", dans Journal of Symbolic Logic, 9 (1944), 33-41
- L. Kirby et J. Paris, " Accessible independence results for Peano arithemtic ", dans Bull. London. Math. Soc., 14 (1982), 285-93
- Patrick Dehornoy, " L'infini est-il nécessaire ? ", dans Pour la Science, 278 (2000), 102-106