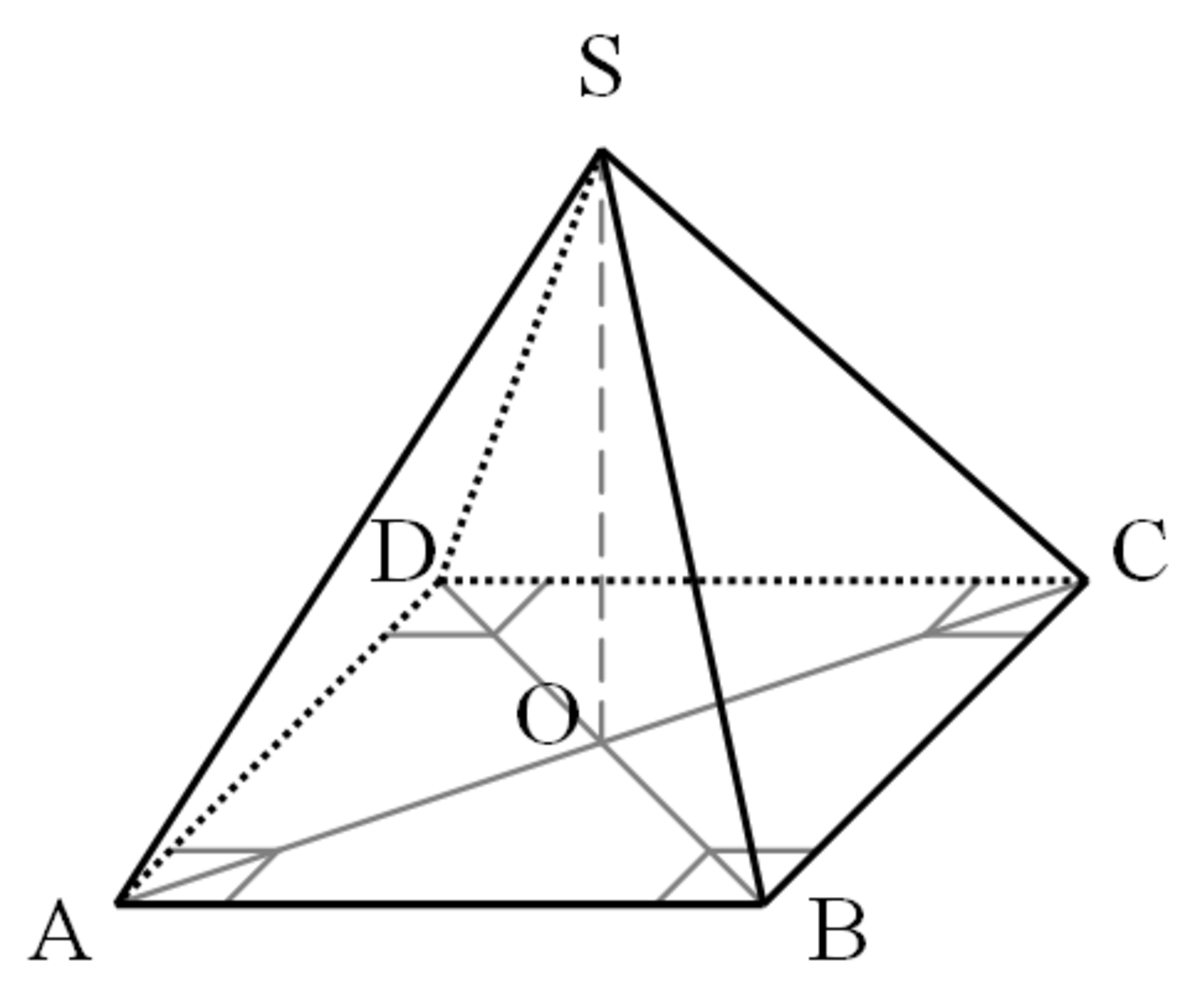
Pyramide - Définition

Cet article traite du polyèdre pyramide (une forme à trois dimensions); pour d'autres versions incluant les pyramides architecturale.

Ensemble des pyramides
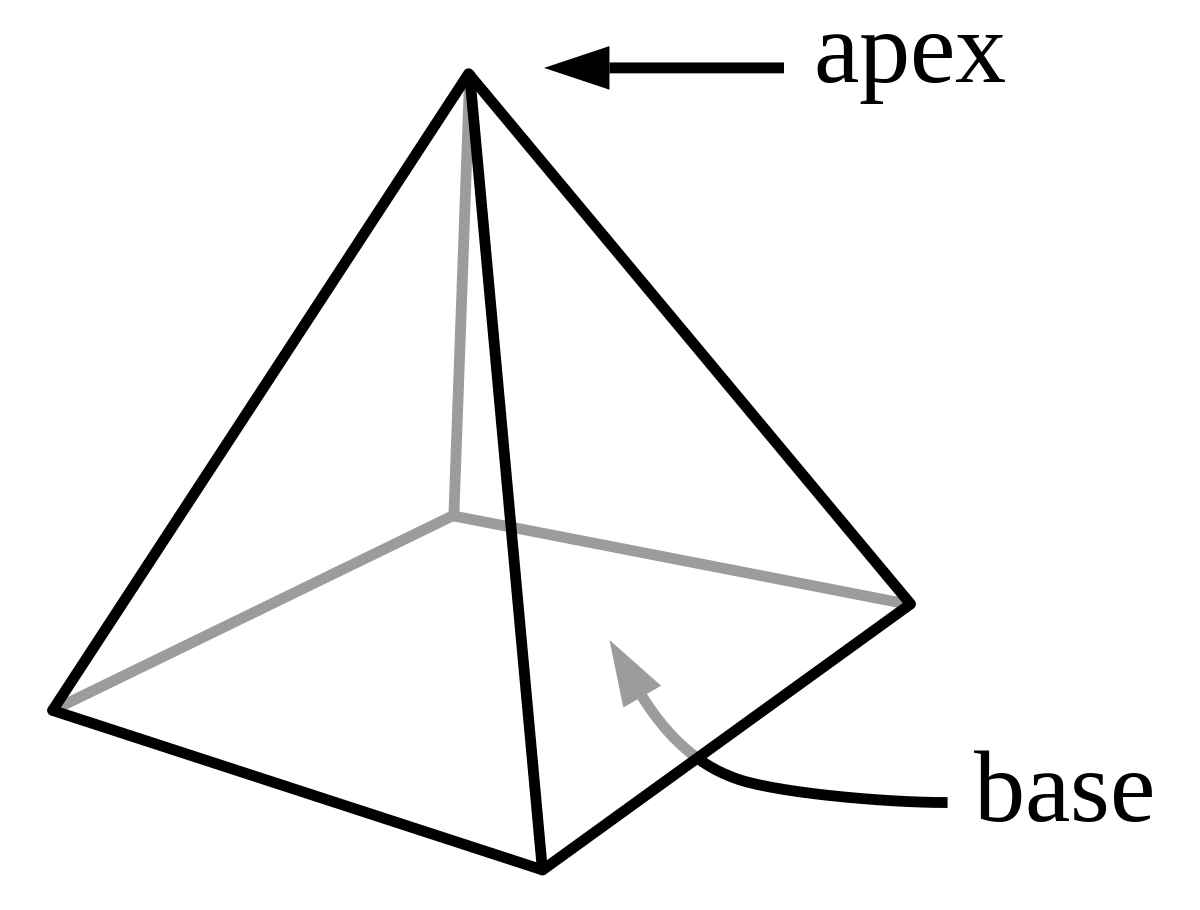
Faces	n triangles, 1 n-gone
Arêtes	2n
Sommets	n+1
Groupe de symétrie	Cnv
Polyèdre dual	Auto-duaux
Propriétés	convexe

Une pyramide (du grec pyramis) à n cotés est un polyèdre formé en reliant une base polygonale de n cotés à un point, appelé l'apex, par n faces triangulaires (n ≥ 3). En d'autres mots, c'est un solide conique avec une base polygonale. Ce sont des grecs qui ont donné le nom "Pyramide", en comparant les momuments égyptiens avec une de leurs patisseries appelée "pyramis", et de forme similaire !

Lorsque cela n'est pas précisé, la base est généralement supposée carrée. Pour une pyramide triangulaire chaque face peut servir de base, avec le sommet opposé pour apex. Le tétraèdre régulier, un des solides de Platon, est une pyramide triangulaire. Les pyramides carrées et pentagonales peuvent aussi être construites avec toutes les faces régulières, et par conséquent sont des solides de Johnson. Toutes les pyramides sont des auto-duaux.

Les pyramides sont une sous-classes des prismatoïdes.

Volume

Le volume d'une pyramide est où A est l'aire de la base et h la hauteur de la base à l'apex. Ceci est valable pour toute localisation de l'apex, à condition que h soit mesuré comme la distance perpendiculaire à partir du plan qui contient la base.

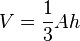
Aire de la surface

L'aire de la surface d'une pyramide régulière est où A_b est l'aire de la base, p est le périmère de la base et s est la hauteur de la pente le long de la bisectrice d'une face (ie la longueur à partir du milieu d'une arête quelconque de la base jusqu'à l'apex).

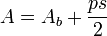
Pyramides avec des faces polygonales

Si toutes les faces sont des polygones réguliers, la base de la pyramide peut être un polygone régulier de 3, 4 ou 5 cotés :

Nom	Tétraèdre	Pyramide carrée	Pyramide pentagonale
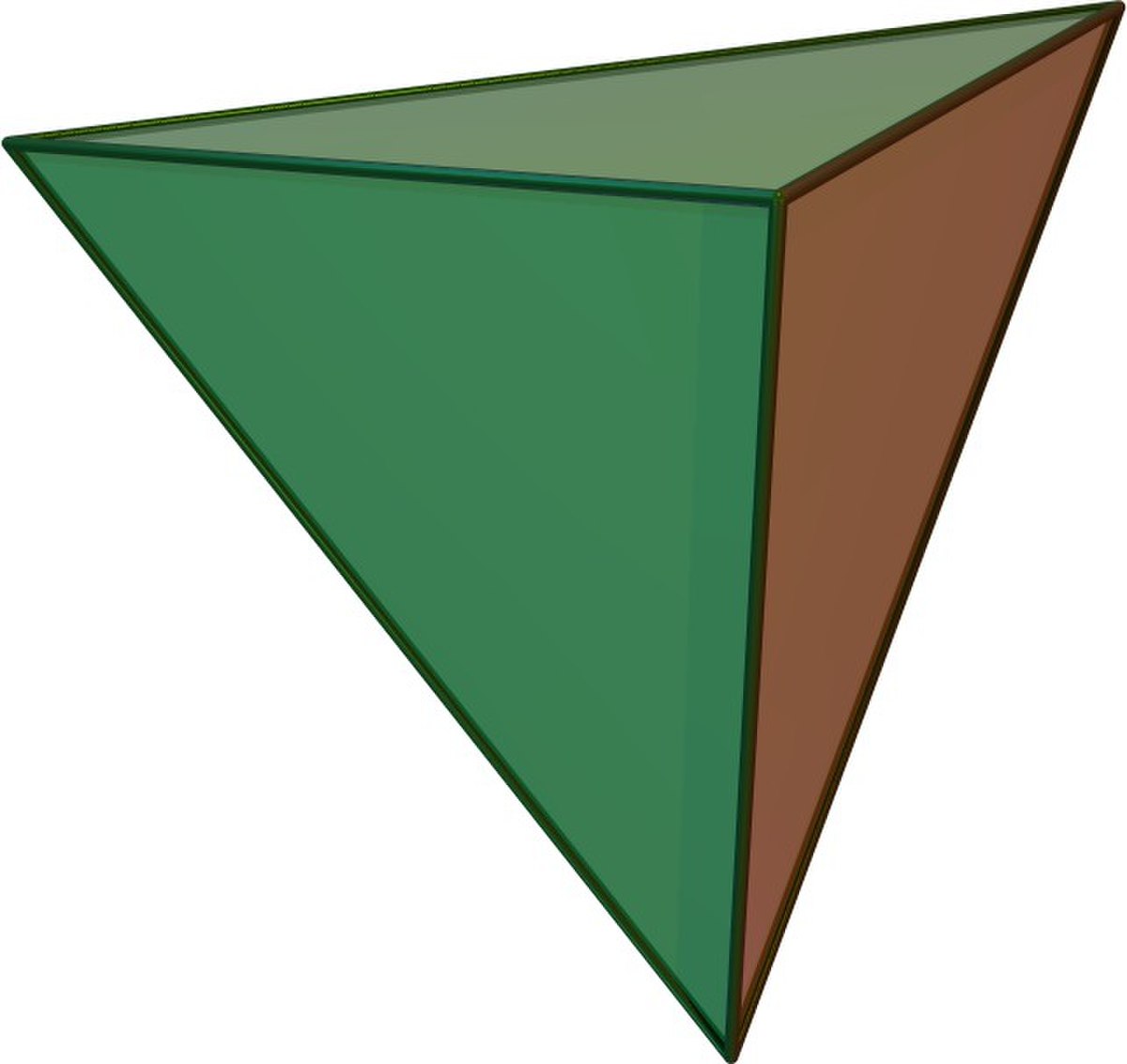
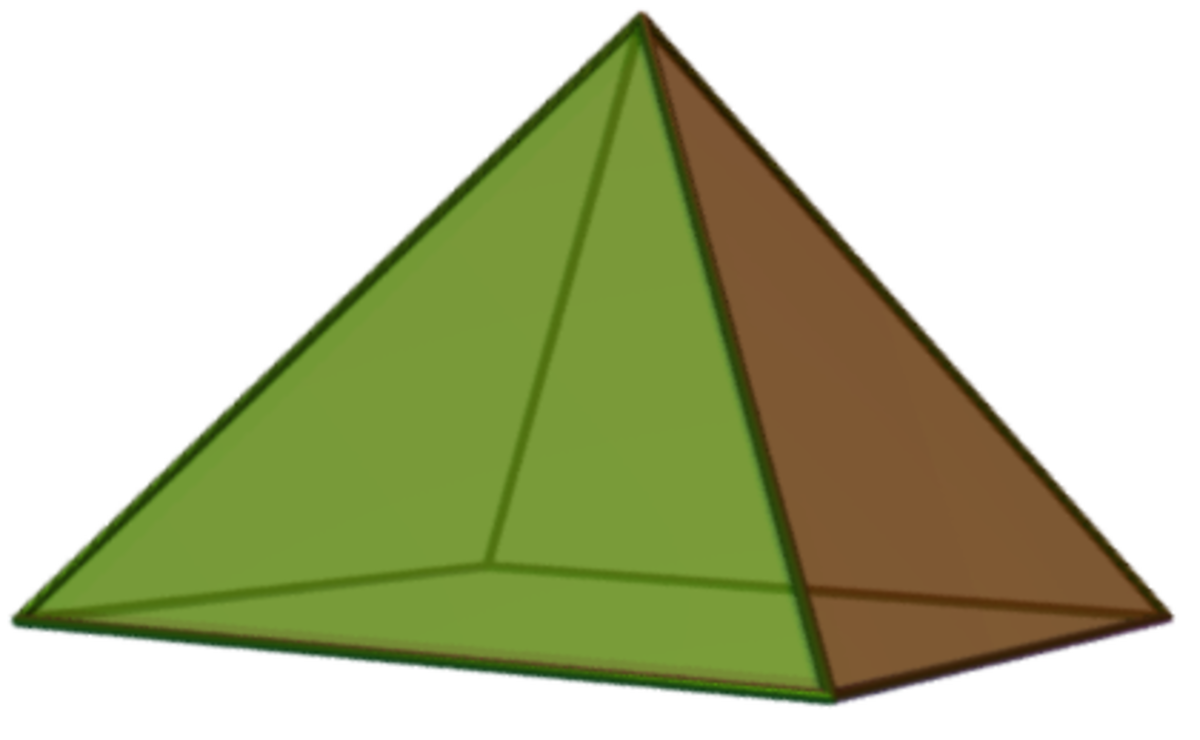
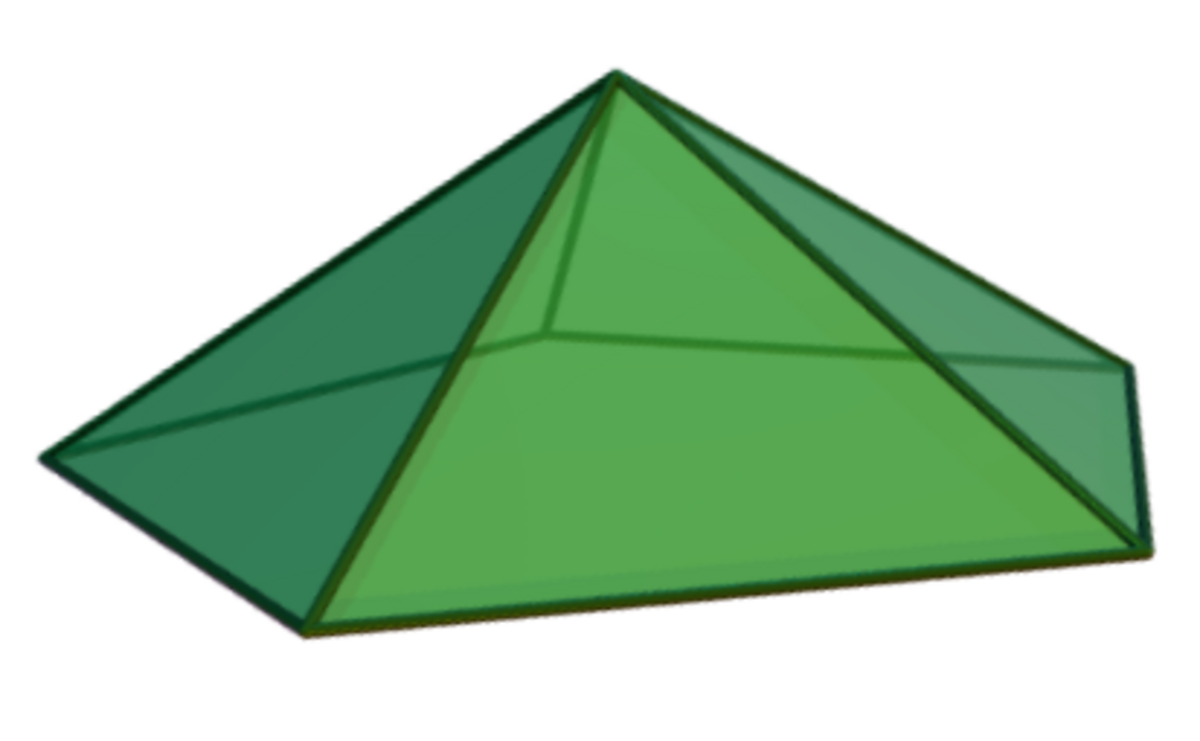
Classe	Solide de Platon	Solide de Johnson (J1)	Solide de Johnson (J2)
Base	Triangle équilatéral	Carré	Pentagone régulier
Groupe de symétrie	Td	C4v	C5v

Le centre géométrique d'une pyramide carrée est localisé sur l'axe de symétrie, à un quart de la base vers l'apex.

Symétrie

Si la base est régulière et l'apex est au-dessus du centre, le groupe de symétrie d'une pyramide à n cotés est C_nv d'ordre 2n, excepté dans le cas d'un tétraèdre régulier, qui possède le groupe de symétrie plus grand T_d d'ordre 24, qui a quatre versions de C_3v pour sous-groupes. Le groupe de rotation est C_n d'ordre n, excepté dans le cas d'un tétraèdre régulier, qui possède le groupe de rotation plus grand T d'ordre 12, qui a quatre versions de C₃ pour sous-groupes.

Symbolique

La forme pyramidale serait magique, et augmenterait certaines qualités en elle, à un endroit précis.