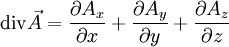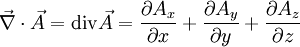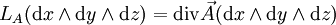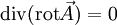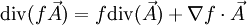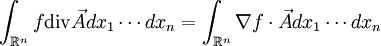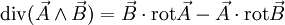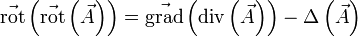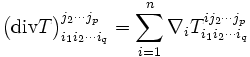Divergence (mathématiques) - Définition

L'opérateur divergence est un opérateur différentiel linéaire aux dérivées partielles premières, souvent utilisé en physique, notamment pour exprimer des lois de conservation. Il transforme un champ vectoriel en un champ scalaire (c’est-à-dire en une fonction) et plus généralement un champ tensoriel d'ordre k en un champ d'ordre k − 1.

Divergence d'un champ de vecteurs

En dimension 3 et en coordonnées cartésiennes, on définit la divergence d'un champ de vecteurs par la relation

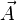
Formellement, l'opérateur divergence appliqué à un champ vectoriel est aussi le produit scalaire du vecteur nabla par le vecteur .

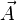
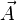
Il revient au même de dire que .

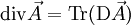
Ici, le champ est considéré comme une application de dans lui même, et désigne sa différentielle, dont on prend la trace – c’est-à-dire la trace de la matrice jacobienne.

Cette dernière présentation a l'avantage d'être indépendante du choix de la base. Tout ce qui précède est aussi valable sur

Exemple

Si est un champ linéaire, c’est-à-dire si , sa divergence est égale à . C'est la trace de la matrice formée par les nombres a_ij ( ).

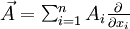
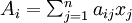
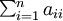
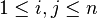
Interprétation de la divergence

La divergence s'interprète en termes de flux. Si D est un domaine de de bord S, le flux de à travers S est égal à l'intégrale sur D de la divergence, d'après le théorème de Stokes.

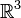
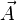
Une interprétation voisine est la suivante. Soit φ_t le flot du champ (c’est-à-dire la valeur au temps t de la solution du système différentiel qui vaut x en 0) on a

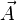
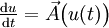
(on a désigné par L_A l'opérateur dérivée de Lie ; pour les détails et un énoncé plus général, voir opérateur de Laplace-Beltrami).

En particulier, le flot de conserve le volume (c’est-à-dire pour tout domaine D) si et seulement si la divergence est partout nulle. Le volume augmente si la divergence est positive, diminue si elle est négative.

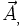
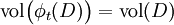
Plus généralement, la divergence rend compte de la variation infinitésimale du volume (ou de la charge électrique) autour d'un point, ce qui explique son intervention dans les équations de la mécanique des fluides ou les équations de Maxwell.

Formulaire commenté

Cette formule est particulière à la dimension 3. Elle signifie qu'un champ rotationnel est à divergence nulle. Inversement, si un champ de vecteurs sur un ouvert étoilé de est à divergence nulle, il existe un champ tel que . (on dit alors que est un potentiel vecteur). Cette propriété, une fois convenablement interprétée en termes de formes différentielles, est une application directe du lemme de Poincaré).

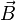
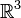
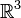
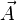
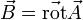
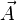
Attention. Le champ newtonien est à divergence nulle, mais il n'existe pas de champ de vecteurs tel que . En effet, si tel était le cas, son flux à travers toute surface fermée serait nul, alors que son flux à travers les sphères centrées à l'origine vaut 4π. En fait, ce champ n'est défini que sur l'espace privé de l'origine, qui n'est pas un ouvert étoilé : le lemme de Poincaré ne s'applique pas.

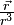
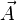
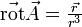
D'après le théorème de Stokes, l'intégrale sur de la divergence d'un champ de vecteurs nul en dehors d'une partie bornée est nulle. Par conséquent, si f est une fonction lisse et un champ de vecteurs, tous deux nuls en dehors d'une partie bornée (cette condition assurant que les intégrales ont un sens),

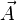
Cette propriété s'interprète de la façon suivante. Soient et respectivement les espaces vectoriels des fonctions lisses et des champs de vecteurs sur . On les munit des produits scalaires

et

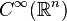
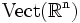
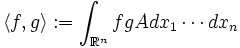
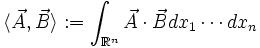
Alors , ce qui permet de voir l'opérateur divergence comme le transposé (au signe près) de l'opérateur gradient.

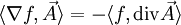
Cette interprétation de la divergence présente l'avantage de se généraliser aussi bien aux variétés riemanniennes qu'aux tenseurs.

Une application typique de cette formule est le théorème de Poynting en électromagnétisme.

Ces relations, très utilisées en analyse vectorielle, se comprennent mieux dans le cadre des formes différentielles.

Lois de conservation s'exprimant en termes de divergence

• En électromagnétisme, si est le vecteur courant et ρ la densité de charge électrique,

.

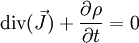
• En mécanique des fluides, si ρ est la masse volumique en un point et le champ des vecteurs vitesse,

(équation de continuité).

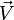
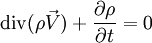
• D'autres lois de conservation font intervenir la divergence de tenseurs d'ordre 2, comme la conservation de la quantité de mouvement en mécanique des fluides.

En relativité générale, la divergence du tenseur énergie-impulsion est nulle.

Divergence d'un tenseur

Cas des espaces euclidiens

Un tenseur de type (p,q)(p-contravariant et q- covariant) est donné par ses coordonnées . Sa dérivée covariante est alors par définition le tenseur de type (p,q+1) donné par (on a désigné par l'opérateur de dérivation par rapport à la i-ième variable). La divergence est le tenseur de type (p-1,q) défini par

(l'utilisation de la convention d'Einstein permettrait d'omettre le symbole de sommation}

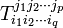
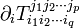
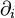
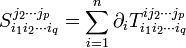
Exemple La divergence du tenseur (qui est de type (2,0)) est le champ de vecteurs

avec

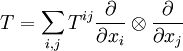
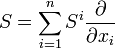
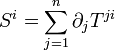
Cas général

Cette définition s'étend pratiquement mot pour mot aux tenseurs sur une variété munie d'une connexion. Dans les formules précédentes, on remplace la différentiation par l'opérateur de différentiation covariante , qui à partir d'un tenseur de type (p,q) donne un tenseur de type (p,q+1), puis on pose

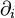
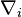
Le cas le plus important est celui des variétés riemanniennes ou pseudo-riemanniennes, munies de leur connexion de Levi-Civita. La métrique permet d'identifier entre eux les tenseurs de même ordre total p+q. La dérivée d'un tenseur d'ordre k sera un tenseur d'ordre k-1.

Les cas les plus utilisés (avec celui des champs de vecteurs vu plus haut) sont ceux des tenseurs symétriques d'ordre 2 et des formes différentielles.

Bibliographie

• Yvonne Choquet-Bruhat & Cécile deWitt-Morette ; Analysis, Manifolds & Physics - Part I: Basics, North-Holland/Elsevier (2ème édition révisée - 1982), ISBN 0-444-86017-7.
• Richard Feynman ; Cours de Physique. Electromagnétisme I, ch. 2 et 3, InterEditions, ISBN 2-72960028-0
• Jacques Lafontaine ; Introduction aux variétés différentielles, Presses Universitaires de Grenoble 1996
• François Rouvière, Petit guide de calcul différentiel à l'usage de la licence et de l'agrégation, Cassini 1999, ISBN 2-84225-008-7