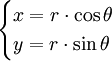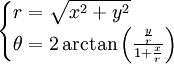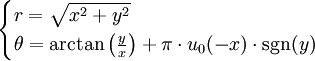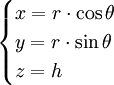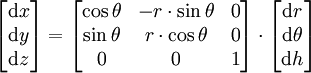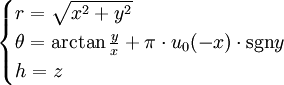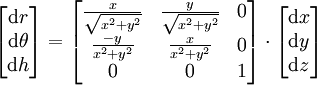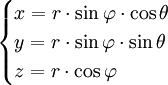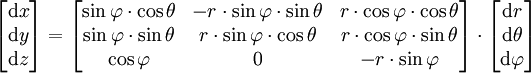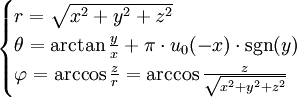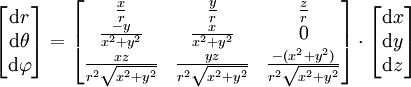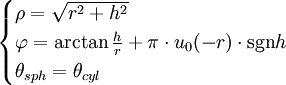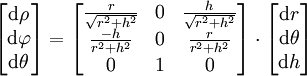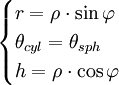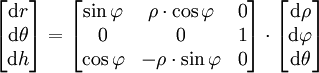Coordonnées polaires - Définition

Les systèmes de coordonnées polaires dans et sont des systèmes de coordonnées particulièrement adaptées pour l'écriture des rotations ou des homothéties.

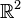
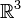
En mécanique classique, elles interviennent naturellement dans tous les problèmes présentant une symétrie de rotation en l'origine, à l'instar du champ gravitationnel d'une boule de densité volumique massique uniforme.

Coordonnées circulaires (coordonnées polaires dans le plan)

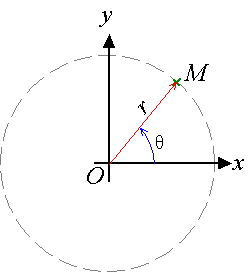
Les coordonnées polaires d'un point M du plan vectoriel orienté (d'origine O) sont la donnée conjointe de :

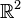
• la distance à l'origine r = OM

• et un angle θ = (OA,OM) où A est un point arbitraire différent de O.

Remarque : il n'y a pas unicité dans la définition des coordonnées polaires : on dispose d'une certaine liberté quant au choix de la coordonnée angulaire θ. Entre autres choses :

• On peut rajouter à θ un multiple entier de 2π
• On peut remplacer r par -r en rajoutant π.

Si on veut un choix univoque de r et θ (ce qui n'est pas toujours judicieux), il faut abandonner le point 0. Pour les autres points, on peut imposer r>0 et θ appartenant à ]-π,π] par exemple.

Relations avec les coordonnées cartésiennes

Désignons par (x,y) les coordonnées cartésiennes du point M et par (r,θ) ses coordonnées polaires. Le passage d'un système de coordonnées à l'autre est donné par les formules suivantes :

Une autre formule possible (qui revient à séparer des cas, et qui pose encore des problèmes pour les cas limites)

où u₀ est la fonction de Heaviside qui vaut 0 si x est strictement négatif et 1 si x est positif (ou nul), et sgn(y) est le signe de y (-1 si y est négatif, +1 si y est positif).

Difféomorphisme, revêtement

L'application est un difféomorphisme local.

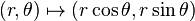
Le revêtement universel de est .

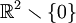
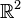
Formulaire physique

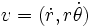
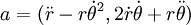
Coordonnées cylindriques

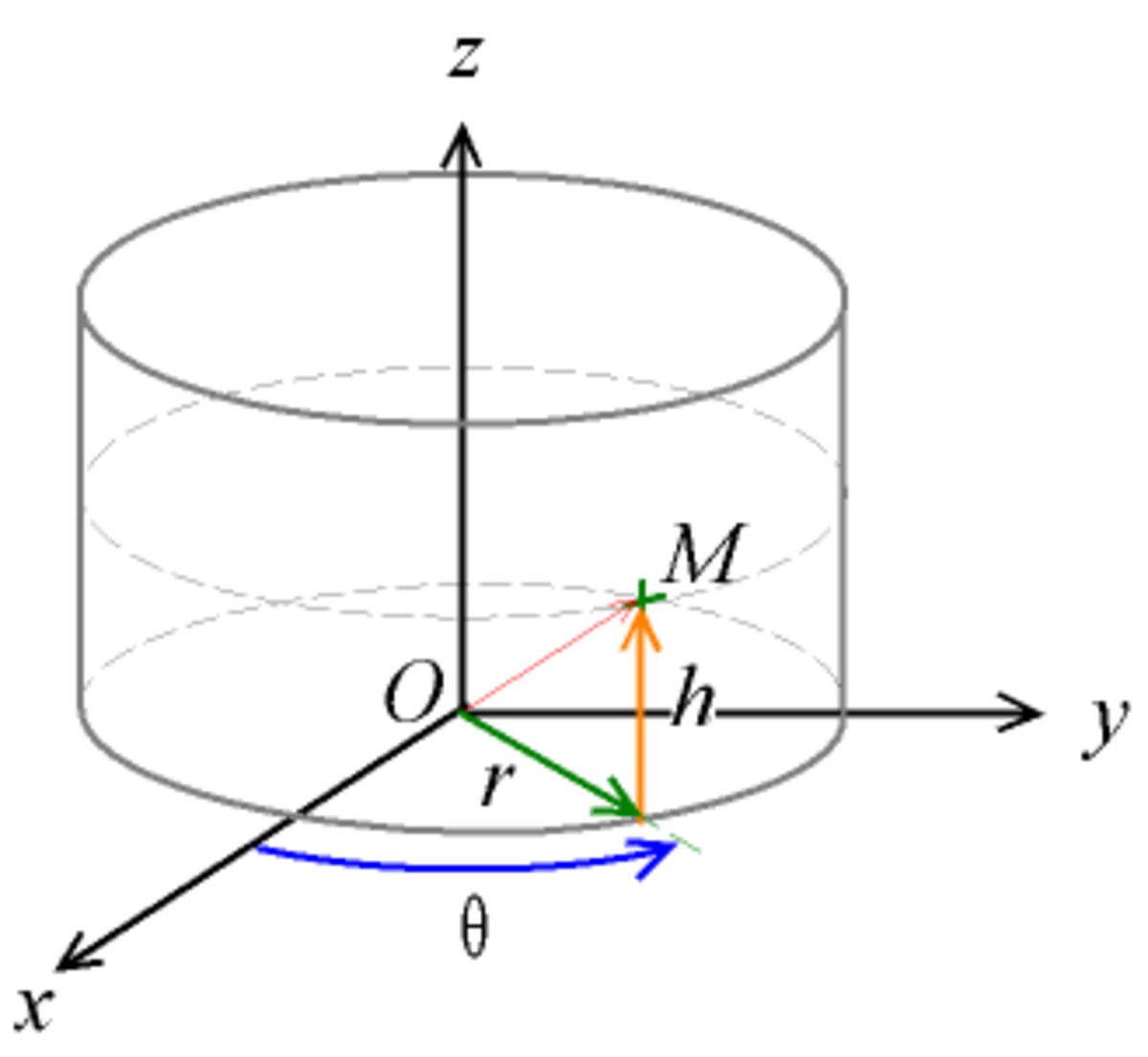
Dans l'espace à trois dimensions, un point M est repéré par

• la distance r de l'origine à sa projection sur Oxy ;
• l'angle θ que fait la projection du vecteur sur le plan Oxy par rapport à Ox ;
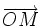
• la hauteur h du point par rapport au plan Oxy.

Relations avec les coordonnées cartésiennes

Le passage des coordonnées cylindriques aux coordonnées cartésiennes (x,y,z) se fait par :

soit en différentiant

Dans l'autre sens :

et en différentiant :

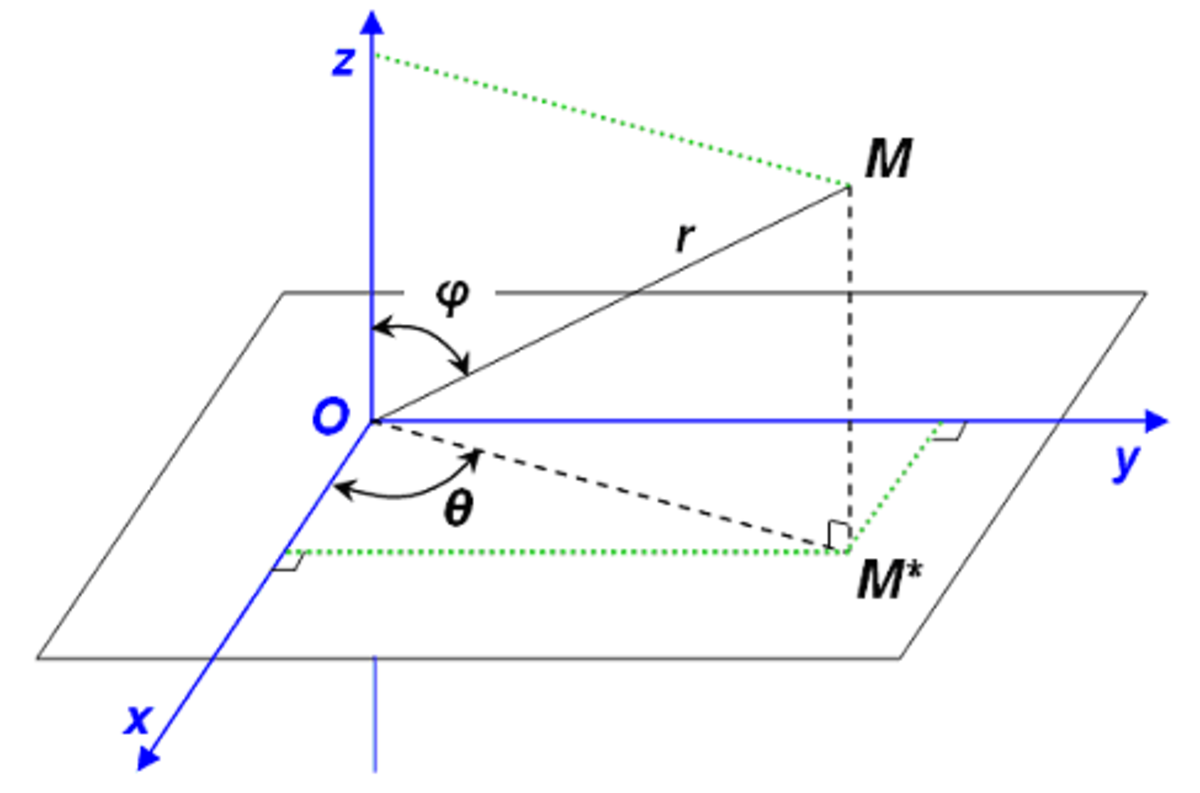
Coordonnées sphériques

Les coordonnées sphériques d'un point M de l'espace euclidien R³ sont la donnée conjointe de :

• la distance r = OM à l'origine du repère ;
• deux angles, θ et φ, permettant de repérer le point M sur la sphère de centre O et de rayon r.

Il existe plusieurs façons de définir ces angles. La définition développée ci après prend θ azimutal (ou longitudinal) et φ colatitudinal. Pour des applications en physique, il est plutôt d'usage de prendre φ azimutal, et θ colatitudinal. Ainsi :

• l'angle θ est celui que fait la projection du vecteur sur le plan Oxy par rapport à Ox ;
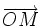
• l'angle φ est celui que fait le vecteur par rapport à Oz.

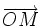
Remarque: On peut également prendre pour défintion de l'angle φ celui que fait le vecteur par rapport à Ox, Ce qui changerait toutes les relations qui vont suivre.

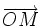
Relations avec les coordonnées cartésiennes

Le passage des coordonnées sphériques aux coordonnées cartésiennes (x,y,z) se fait par :

si l'on différentie, on obtient

Dans l'autre sens :

et en différentiant :

Relations avec les coordonnées cylindriques

Le passage des coordonnées cylindriques (r,θ_cyl,h) aux coordonnées sphériques (ρ,θ_sph,φ) se fait par :

soit en dérivant :

(on a θ = θ_cyl = θ_sph)

Le passage des coordonnées sphériques (ρ,θ_sph,φ) aux coordonnées cylindriques (r,θ_cyl,h) se fait par :

soit en dérivant :

(même remarque que ci-dessus).

Généralisation des coordonnées sphériques : angles d'Euler

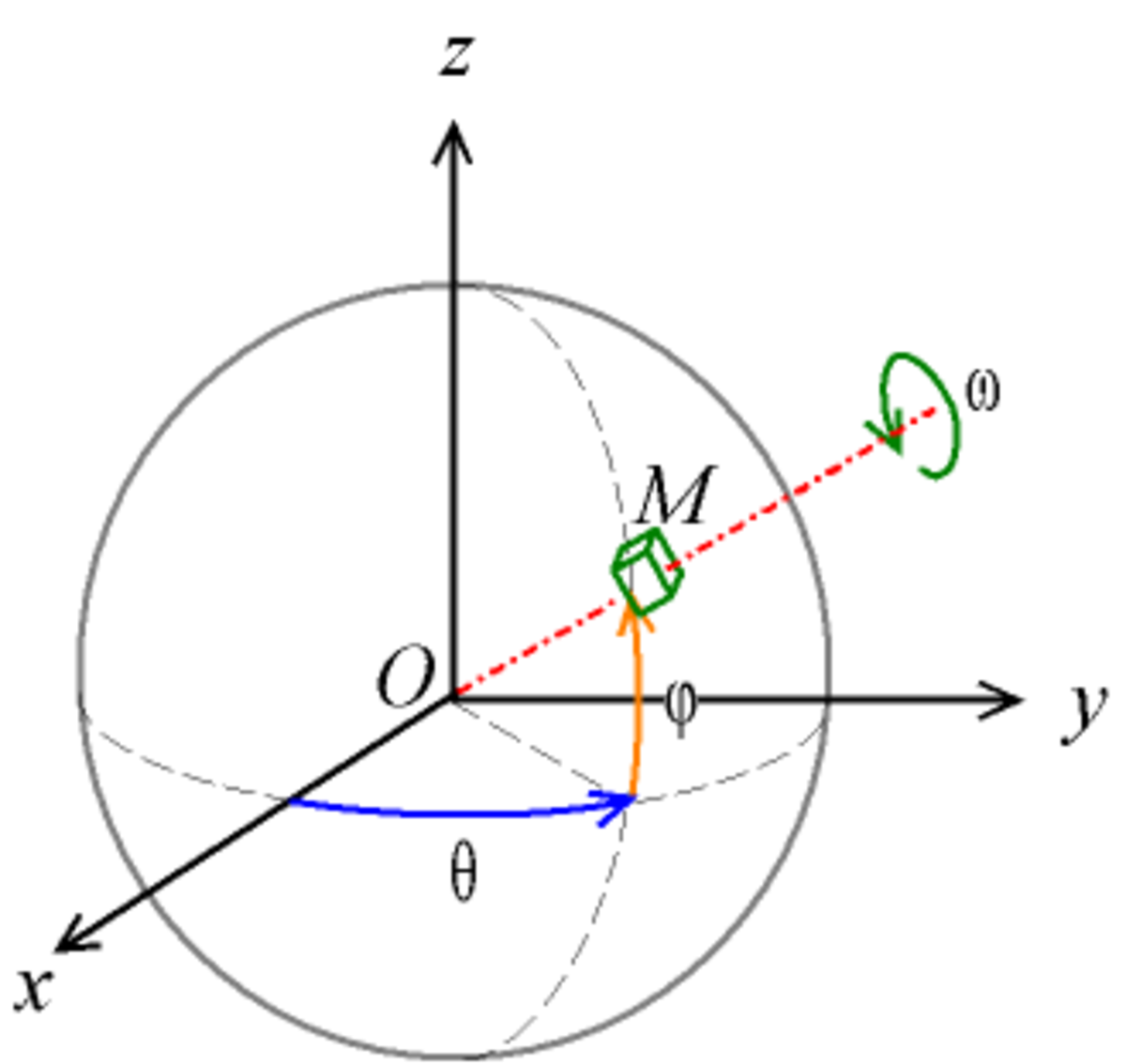
Si l'on ne s'intéresse qu'à l'orientation dans l'espace, on n'utilise pas ρ, par contre, il faut définir un troisième angle ω qui est la rotation autour de l'axe OM. Cette généralisation des coordonnées sphériques (θ,φ,ω) est en fait une définition des angles d'Euler, mais avec des rotations différentes des rotations habituelles :

• rotation d'un angle θ autour de Oz, Oxyz devient Ouvz ;
• rotation d'un angle φ autour de Ov, Ouvz devient Ox'vw ;
• rotation d'un angle ω autour de Ox' , Ox'vw devient Ox'y'z' .

Cette définition n'est pas utilisée, mais elle est présentée ici à titre pédagogique : elle permet de comprendre simplement la notion d'orientation et d'angle d'Euler lorsque l'on a compris celle de coordonnées sphériques.