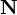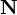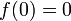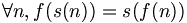Axiomes de Peano - Définition

Les axiomes de Peano sont, en mathématiques, un ensemble d'axiomes de second ordre proposés par Giuseppe Peano pour définir l'arithmétique [1].

Axiomes

La définition axiomatique des entiers naturels de Peano est usuellement décrite informellement par cinq axiomes :

1. l'élément appelé zéro et noté: 0, est un entier naturel.
2. Tout entier naturel n a un unique successeur, noté s(n) ou Sn.
3. Aucun entier naturel n'a 0 pour successeur.
4. Deux entiers naturels ayant même successeur sont égaux.
5. Si un ensemble d'entiers naturels contient 0 et contient le successeur de chacun de ses éléments, alors cet ensemble est égal à .

Le premier axiome permet de poser que l'ensemble des entiers naturels n'est pas vide, le troisième qu'il possède un premier élément et le cinquième qu'il vérifie le principe de récurrence.

De façon plus formelle, le triplet satisfait les propriétés suivantes :

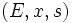
1. E est un ensemble, x est un élement de E, s est une application de E dans lui-même.
2. 
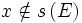
3. s est injective
4. Tout sous-ensemble F de E contenant x et stable par s (c'est-à-dire que ) est égal à E.

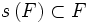
Une telle structure est appelée structure de Dedekind-Peano (d'après le mathématicien Richard Dedekind) [2]

Arithmétique de Peano

L'arithmétique de Peano est la restriction des axiomes de Peano au langage de l'arithmétique du premier ordre . Les variables du langage désignent des objets du domaine d'interprétation, ici des entiers. Dans ce langage du premier ordre, on ne dispose pas de variables pour les ensembles d'entiers, et on ne peut quantifier sur ces ensembles. On ne peut donc pas exprimer directement la récurrence par un énoncé tel que celui du paragraphe précédent (" tout sous-ensemble ... "). On considère alors qu'un sous-ensemble de est exprimé par une propriété de ses éléments, propriété que l'on écrit dans le langage de l'arithmétique.

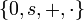
Les axiomes de Peano deviennent alors les 7 axiomes suivants, auxquels s'ajoute, pour la récurrence, un schéma d'axiomes, qui représente une infinité dénombrable d'axiomes (un axiome pour chaque formule du langage) :

1. 
2. 
3. 
4. 
5. 
6. 
7. 
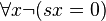
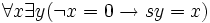
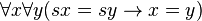
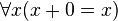
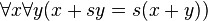
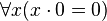
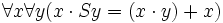
8. Pour toute formule à n + 1 variables libres,

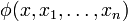
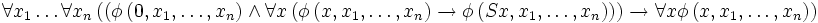
Le schéma d'axiomes exprime bien la récurrence : dans la formule , les variables sont des paramètres, que l'on peut remplacer par des entiers arbitraires . L'axiome pour la formule devient, appliqué à  :

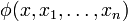
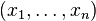
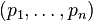
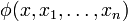
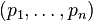
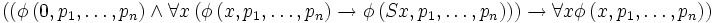
Ce qui exprime bien que, si l'ensemble contient 0, et s'il contient le successeur de chacun de ses éléments, c'est .

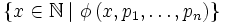
Cependant, le schéma d'axiomes ne donne plus cette propriété que pour les sous-ensembles de qui se définissent dans le langage de l'arithmétique du premier ordre : une infinité dénombrable de sous-ensembles de .

On peut montrer que l'arithmétique de Peano ne peut être finiment axiomatisée, à moins de modifier le langage. Cela n'a donc pas forcément grand sens de chercher à minimiser les axiomes. On peut tout de même remarquer que l'axiome 2 pourrait être éliminé. Il se démontre par récurrence, une récurrence assez singulière, puisqu'il faut bien distinguer le cas 0 du cas successeur, mais que dans ce dernier cas, l'hypothèse de récurrence n'est pas utile.

Existence et unicité

L'existence d'une structure de Dedekind-Peano peut être établie par une construction très usuelle dans le cadre de la théorie des ensembles :

• On pose 0 = ∅.
• On définit la " fonction " (au sens intuitif) successeur s en posant, pour tout ensemble a, . On remarque que pour tous ensembles a et b :

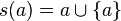
s(a) ≠ 0  ;   s(a) = s(b) ⇒ a = b.

• Un ensemble A est dit inductif s'il contient 0 est s'il est clos par successeur, c'est-à-dire que si , alors .
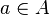
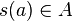
• L'existence d'au moins un ensemble inductif est assurée par l'axiome de l'infini. On définit alors la structure  : est l'intersection de tous les ensembles inductifs et est la restriction de s à . Cette structure satisfait les axiomes pré-cités (entre autres il est bien ordonné). On peut définir comme l'ensemble des entiers naturels.

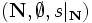
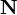
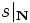
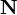
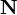
Cet ensemble est aussi l'ensemble des ordinaux de von Neumann finis. Cette construction de N n'est pas vraiment canonique, l'essentiel est que 0 ne soit jamais un successeur et que le successeur soit injectif (et encore, cela suffirait que ce soit sur l'ensemble obtenu), mais elle permet de construire de façon simple et uniforme un ensemble représentant chaque cardinalité finie (l'entier n ainsi construit a, en tant qu'ensemble, pour cardinal n), l'axiome de l'infini permettant de prouver qu'ils forment un ensemble.

Deux structures de Dedekind-Peano et sont dites isomorphes s'il existe une bijection telle que φ(x) = y et φf = gφ. On peut montrer que toutes les structures de Dedekind-Peano sont isomorphes.

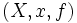
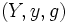
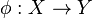
On trouve souvent la notation pour l'ensemble des entiers naturels.

Opérations et ordre

L'addition et la multiplication sont définies sur par les axiomes de Peano.

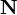
L'addition sur est définie récursivement en posant a + 0 = a et a + s(b) = s(a + b) pour tout a et b. est ainsi un monoïde commutatif d'élément neutre 0. Ce monoïde peut être plongé dans un groupe. Le plus petit groupe le contenant est celui des nombres entiers.

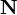
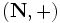
Puisque s(0) = 1, s(b) = s(b + 0) = b + s(0) = b + 1. Le successeur de b est simplement b + 1.

De façon analogue, en supposant que l'addition a été définie, la multiplication sur est définie en posant et . est ainsi un monoïde commutatif d'élement neutre 1.

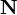
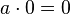
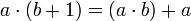
Il est finalement possible de définir un ordre total sur en posant que s'il existe un nombre c tel que a + c = b. Alors muni de cet ordre est un bien ordonné : tout ensemble non vide de nombres naturels possède un plus petit élément.

Cohérence

En vertu du second théorème d'incomplétude de Gödel, la non-contradiction de ces axiomes entre eux n'est pas conséquence de ces seuls axiomes : on ne peut pas prouver la cohérence de l'arithmétique dans l'arithmétique.

Une structure de Dedekind-Peano est un modèle de ces axiomes. La construction ci-dessus fournit donc une preuve de cohérence des axiomes relativement à une théorie dans laquelle on peut définir ces structures, et formaliser la preuve de correction, par exemple la théorie axiomatique des ensembles de Ernst Zermelo. Il existe également des preuves de cohérence relative, notamment celle de Gerhard Gentzen qui fournit une mesure précise de la " force " de l'arithmétique : il suffit d'ajouter un principe d'induction jusqu'à l'ordinal dénombrable ε₀ pour pouvoir démontrer la cohérence de l'arithmétique.

Modèles non standard

Un modèle de l'arithmétique de Peano qui n'est pas une structure de Dedekind-Peano, et n'est donc pas isomorphe à est dit " non standard ".

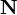
Tout modèle non standard de l'arithmétique contient les entiers naturels, que l'on appelle alors, entiers " standard ", et qui sont les éléments du modèles que l'on peut désigner par des termes du langage, les autres éléments du modèle sont alors appelés entiers non standard.

Plus précisément si est un modèle non standard de l'arithmétique, alors il existe une injection f de dans telle que :

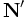
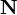
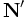
et l'image de f est ce que l'on appelle l'ensemble des entiers standard du modèle.

Il n'est pas possible de distinguer les entiers standard des entiers non standard dans le langage de l'arithmétique, puisque si un prédicat permettait de caractériser les entiers standard, le schéma de récurrence particularisé à ce prédicat ne serait pas valide. On " sort " donc de l'arithmétique de Peano dès que l'on raisonne sur ces notions dans un modèle non standard. Mais, on peut se servir bien entendu du fait que les axiomes de Peano restent valides dans ce modèle. On montre par exemple facilement qu'un entier non standard est nécessairement supérieur à un entier standard. La totalité de l'ordre (défini par l'addition, voir ci-dessus), reste valide. Si un entier non standard était plus petit qu'un entier standard, on montrerait par injectivité du successeur et récurrence qu'il existe un entier non standard plus petit que 0, et 0 serait un successeur. Encore plus simplement, on montre qu'il ne peut y avoir de plus petit entier non standard, puisque tout entier non nul est un successeur.

Existence des modèles non standard

• Le théorème de compacité et le théorème de Löwenheim-Skolem assurent qu'il existe des modèles dénombrables non standard de l'arithmétique de Peano qui vérifient exactement les mêmes énoncés du premier ordre que . Abraham Robinson fonde l'analyse non standard sur un modèle de l'arithmétique vérifiant en particulier cette condition.

• Il existe également des modèles non standard qui vérifient des énoncés du premier ordre faux dans (en plus, rappelons-le, de tous les énoncés démontrables dans Peano, par définition de la notion de modèle). Un énoncé vrai dans n'est pas démontrable dans l'arithmétique de Peano, si et seulement s'il existe un modèle non standard dans lequel cet énoncé est faux. Les théorèmes d'incomplétude de Gödel ont donc pour conséquence l'existence de tels modèles (qui vérifient une formule exprimant que l'arithmétique de Peano est incohérente !). A contrario, on peut utiliser de tels modèles pour montrer que certains énoncés ne sont pas démontrables dans l'arithmétique de Peano.