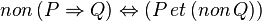Logique (mathématiques élémentaires) - Définition

Cet article fait partie de la série Mathématiques élémentaires

Algèbre

Analyse

Arithmétique

Géométrie

Logique

Probabilité

Statistique

La logique est la base des démonstrations en mathématique. Bien qu'elle apparaisse de manière cachée dans toute l'argumentation mathématique, elle est indispensable à la compréhension de théorème. Elle se formalise sous forme de table de vérité dans l'algèbre de Boole

Aspect expérimental

Implications et équivalences

En logique, on découvre des conditions nécessaires, des conditions suffisantes, des implications, des équivalences, des réciproques et des contraposées. Chacun de ces mots correspond à un lien logique entre des propositions.

Dans l'affirmation:

si ABCD est un carré alors ABCD est un parallélogramme.

On dit que

• ABCD est un carré est une condition suffisante pour que ABCD soit un parallélogramme
• ABCD est un parallélogramme est une condition nécessaire pour que ABCD soit un carré

On écrira ABCD est un carré ABCD est un parallélogramme. Cette relation s'appelle une implication.

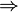
On peut remarquer que

• ABCD est un parallélogramme n'est pas une condition suffisante pour que ABCD soit un carré
• ABCD est un carré n'est pas une condition nécessaire pour que ABCD soit un parallélogramme

On remarque donc que l'implication

ABCD est un parallélogramme ABCD est un carré

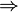
est une implication fausse.

Renverser le sens d'une implication, c'est prendre la réciproque.

Dans le cas de notre exemple, On peut dire que l'implication

"si ABCD est un carré alors ABCD est un parallélogramme"

est une implication juste mais que sa réciproque est fausse.

On remarque que dans une implication, il y a souvent perte d'information entre le premier terme de l'implication et le second.

D'après notre affirmation précédente, on peut remarquer que

si ABCD n'est pas un parallélogramme alors ABCD n'est pas un carré

Inverser le sens de l'implication et prendre la négation des affirmations s'appelle prendre la contraposée de l'implication. Dans tous les cas, si une implication est juste alors sa contraposée est juste.

Lorsque une implication est vraie et que sa réciproque est vraie aussi, on dit que les deux affirmations sont équivalentes:

Par exemple, pour trois points ABC distincts, on a:

• si ABC est un triangle rectangle en A alors AB² + AC² = BC² (première implication)
• si AB² + AC² = BC² alors le triangle est rectangle en A (réciproque)

L'implication et sa réciproque sont vraies, les deux affirmations sont donc équivalentes. On écrira donc

ABC est rectangle en A si et seulement si (abrégé en ssi) AB² + AC² = BC²

que l'on raccourcit parfois en

ABC est rectangle en A AB² + AC² = BC²

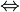
Quantificateurs

En réalité, une affirmation n'est vraie que dans un domaine particulier, il faut donc préciser le domaine de validité et préciser pour quels éléments c'est vrai.

L'affirmation

x² 0

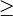
n'a aucun sens hors contexte. En revanche, on peut trouver

• pour tout nombre réel x, x² 0 (qui est une affirmation vraie)
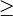
• pour tout complexe x, x² 0 (qui est une affirmation fausse)
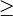
• Il existe des complexes x tels que x² 0 (qui est une affirmation vraie)
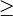
• Il existe des imaginaires purs tels que x² 0 (qui est une affirmation fausse)

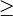
Les précisions "il existe" et "pour tout"" sont appelés des quantificateurs. Souvent sous-entendus dans les raisonnements, ils sont toujours indispensables. On peut remarquer que pour le théorème de Pythagore cité précédemment, il a été précisé, par un quantificateur, le domaine de validité "pour tous points A, B, C distincts".

Contraire

Prendre le contraire d'une affirmation, c'est exprimer la proposition qui sera vraie si et seulement si la précédente est fausse. Le contraire de la phrase

"dans cette salle, toutes les personnes sont des filles"

est

"dans cette salle, il existe au moins un garçon".

Quand on maîtrise bien la logique et les quantificateurs, on sait prendre la négation de toute proposition : il suffit d'inverser les quantificateurs et de prendre la propriété contraire.

Le contraire de

"pour tout réel x, f(x) = f(-x) " (qui traduit la parité d'une fonction définie sur R)

est

"il existe un réel x tel que f(x) f(-x) (qui traduit le fait qu'une fonction définie sur R n'est pas paire)

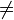
On s'aperçoit ainsi qu'il existe des règles de calcul en logique que l'on peut formaliser à l'aide de tables de vérité

Approche d'une formalisation

Les bases

Soit P une proposition.
On dit que P est vraie ou fausse.

Soit P une propriété à un état. Alors non P est à l'état opposé.

On peut ainsi établir une table de vérité :

P	nonP	non(nonP)
V	F	V
F	V	F

Et ceci montre que P = non non P.

Maintenant, et c'est ce qu'il y a de plus intéressant, concentrons-nous sur les relations :

Prenons les deux relations basiques : " et " et " ou " (il faut que P soit vrai et que Q soit vrai, ou respectivement, que P soit vrai ou Q soit vrai, pour que la relation soit vraie). On dit que R=P.Q=(P et Q) est vraie si tous deux sont vrais à la fois. On dit que R=P+Q=(P ou Q) est vraie si l'un ou l'autre est vrai.

On établit alors la table de vérité :

P	Q	P et Q	P ou Q
F	F	F	F
F	V	F	V
V	F	F	V
V	V	V	V

Soit P et Q deux propositions. Soit R la relation => (il suffit que)

P	Q	P Q
F	F	V
F	V	V
V	F	F
V	V	V

Ceci est la définition de la relation implication.

De même, pour la relation (il faut que)

P	Q	P Q
F	F	V
F	V	F
V	F	V
V	V	V

Enfin, pour que R: <=> soit vrai (équivalence), il faut que => et <= soient vraies :

P	Q	P Q	P Q	P Q
F	F	V	V	V
F	V	V	F	F
V	F	F	V	F
V	V	V	V	V

L'analyse de telles tables nous permet de montrer que, par exemple, dans une démonstration, pour que P<=>Q, il faut et il suffit que P=>Q ET non P => non Q.

En effet :

P	Q	nonP	nonQ	P Q	nonP nonQ	P Q et nonP nonQ	P Q
F	F	V	V	V	V	V	V
F	V	V	F	V	F	F	F
V	F	F	V	F	V	F	F
V	V	F	F	V	V	V	V

On vient là de démontrer que la réciproque d'un théorème pouvait se montrer en partant de l'inverse des hypothèses pour arriver à l'inverse de la conclusion.

De la même façon, il est aisé de montrer avec ces tables de vérité que P=>Q est équivalent à nonP ou Q. On laissera le lecteur faire le tableau afin de s'en convaincre.

La logique est donc à la base des mathématiques, et leur permet de faire toutes les démonstrations nécessaires pour les théorèmes les plus simples comme les plus complexes.

Résultats importants

Notons que les lignes suivantes sont " vraies ". Il s'agit de relations vraies quelles que soient P et Q deux propositions.

• 
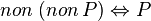
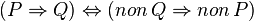
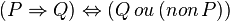
• , le deuxième membre de l'équivalence est souvent appelé la contraposée du premier membre.
• 
• , ce résultat est important lorsqu'on utilise un raisonnement par l'absurde: si on veut prouver une implication, on montre que sa négation conduit à une absurdité.