Univers de Gödel - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

L'univers de Gödel est une solution aux équations de la relativité générale publiée par le mathématicien Kurt Gödel en 1949. Cette solution possède plusieurs propriétés remarquables, quoique physiquement irréalistes, et a été à l'origine de la recherche d'un plus grand nombre de solutions exactes aux équations d'Einstein.

Métrique de l'univers de Gödel

Cette solution décrit un espace quadri-dimensionnel lorentzien (tout comme notre espace-temps) empli de matière non relativiste de pression nulle et d'une constante cosmologique. La métrique (ou l'élément de longueur) de cet espace s'écrit

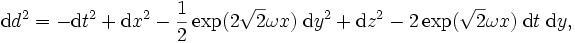
${\rm d} d^2 = - {\rm d} t^2 + {\rm d}x^2 - \frac{1}{2} \exp(2 \sqrt{2} \omega x) \;{\rm d}y^2 + {\rm d} z^2 - 2 \exp(\sqrt{2} \omega x) \;{\rm d}t \;{\rm d} y ,$

où $ω$ est une constante position représentant la vorticité du fluide qui est au repos par rapport aux coordonnées $x$ , $y$ , $z$ . La densité d'énergie $ρ$ du fluide et la constante cosmologique $Λ$ sont reliées à la vorticité par

$4πρ = - Λ = ω 2$

dans un système d'unités tel que la vitesse de la lumière et la constante de gravitation valent 1.

Propriétés

L'univers de Gödel représente un espace homogène, c'est-à-dire que tous ses points sont équivalents.

Sa principale particularité est qu'il comporte des courbes de genre temps fermées. Par le changement de coordonnées

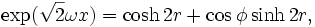
$\exp(\sqrt{2} \omega x) = \cosh 2r + \cos \phi \sinh 2r ,$

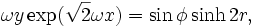
$\omega y \exp(\sqrt{2} \omega x) = \sin \phi \sinh 2r ,$

$\tan \left(\frac{1}{2} (\varphi + \omega t - \sqrt{2} t) \right) = \exp(- 2 r) \tan \frac{1}{2} \varphi,$

l'élément de longueur se réécrit

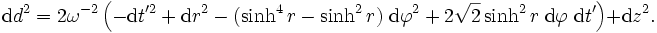
${\rm d} d^2 = 2 \omega^{-2} \left(- {\rm d} t'^2 + {\rm d}r^2 - (\sinh^4 r - \sinh^2 r) \;{\rm d}\varphi^2 + 2 \sqrt{2} \sinh^2 r \;{\rm d} \varphi \;{\rm d}t' \right) + {\rm d} z^2 .$

Le fluide est toujours au repos par rapport aux coordonnées $r$ , $\varphi$ , $z$ et l'espace autour de l'origine est symétrique par rapport à l'axe $r = 0$ . L'espace étant homogène, cette propriété se retrouve pour tous les autres points. En $r = 0$ , le cône de lumière futur est orienté vers le haut, tout comme dans un système de coordonnées polaires ordinaire dans l'espace de Minkowski, et n'inclut pas les lignes de coordonnées de $r$ et $\varphi$ . 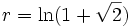À mesure que l'on considère des points pour des valeurs plus grandes de $r$ , les cônes de lumière s'inclinent peu à peu jusqu'à inclure la ligne de coordonnée de $\varphi$ à partir de $r = \ln (1 + \sqrt{2})$ . Les lignes de coordonnées de $\varphi$ sont donc pour les grandes valeurs de $r$ des courbes de genre temps fermées. Pour cette raison, l'espace de Gödel n'est pas considéré comme une solution physiquement acceptable des équations d'Einstein.

Bibliographie

An Example of a New Type of Cosmological Solutions of Einstein's Field Equations of Gravitation, L'article historique de Kurt Gödel, Review of Modern Physics 21, 447–450 (1949)
(en) Stephen W. Hawking et G. F. R. Ellis, The large scale structure of space-time, Cambridge University Press, coll. " Cambridge Monographs on Mathematical Physics ", 1975, 400 pages (ISBN 0521099064), section 5.7, pages 168 à 170.

Liste de tous les modèles cosmologiques