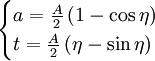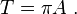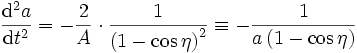Univers fini de Friedmann - Définition

Introduction

Parmi les nombreux modèles cosmologiques de notre Univers, le modèle d’univers fini de Friedmann occupe une place à part parce qu'il est historiquement l'un des premiers à avoir fourni une image physiquement cohérente du cosmos dans le cadre de la nouvelle théorie de la relativité générale d'Einstein.

De plus, sa simplicité intrinsèque et sa richesse font de lui le modèle idéal pour aborder la cosmologie moderne. Cette page est destinée à le présenter en détail. Elle fournira aussi la définition de paramètres cosmologiques importants tels que la constante de Hubble ou la densité critique et servira d'introduction aux problèmes cruciaux de la cosmologie moderne comme le problème de la platitude ou le problème de l'horizon. L'univers fini de Friedmann a une valeur pédagogique précieuse.

Introduction

Le modèle d'univers de Friedmann est le plus simple des modèles cosmologiques satisfaisant aux équations d'Einstein. Conçu en 1922 par Alexander A. Friedmann, ce modèle revêt une importance historique et conceptuelle considérable.

C'est le premier en effet qui a permis à la science d'analyser le cosmos de façon physiquement cohérente en donnant par exemple un sens à la notion de taille, d'âge et de contenu en matière-énergie de l'Univers. En outre, ce modèle prédisait un phénomène dont personne ne pouvait à l'époque (vers 1920) soupçonner l'existence, à savoir l'expansion de l'espace. En observant que toutes les galaxies s'éloignaient de la nôtre, Hubble confirma une dizaine d'années plus tard la réalité de cette expansion et prouva du même coup la justesse de la nouvelle théorie de la relativité générale. En remontant le temps en arrière, cette expansion impliquait qu'à l'origine notre Univers était infiniment condensé, une situation qui conduisait inéluctablement à l'idée du Big Bang. Enfin, également pour la première fois, la science apportait une réponse à la question immémoriale des limites de l'Univers, ce qui constituait un succès extraordinaire de la réflexion humaine. Le modèle homogène fini représente en effet un espace-temps qui, doté de la « courbure » que lui imprime la masse qu'il contient, est dénué de frontières. Il n'est pas contenu dans un espace extérieur : il constitue à lui seul tout temps et tout espace.

On ne peut toutefois pas aisément visualiser cette situation, car notre espace n'a que trois dimensions alors qu'on traite un objet mathématique abstrait : un espace non réel à quatre dimensions.

Bien qu'incomplet, le modèle d'univers de Big Bang homogène fini a initialisé toutes les découvertes cosmologiques modernes et leur a servi de cadre. D'autre part, même s'il n'est accepté aujourd'hui que par un nombre restreint de cosmologistes — mais parmi eux, il y a des noms célèbres comme celui de John Archibald Wheeler — les autres préférant le modèle infini, le modèle fini possède les propriétés principales des univers issus d'un Big Bang, contient tous les points où la théorie rencontre des difficultés et se révèle suffisant à la fois pour comprendre les grandes lignes de la structure de l'Univers et pour poser les problèmes actuels auxquels se trouve confrontée la cosmologie.

Variation du rayon de l'univers avec le temps

En traçant a comme fonction de t et en prenant pour unité sur les deux axes la quantité (A/2) on observe une cycloïde.

La dynamique de la géométrie de l'univers est déterminée par la loi de variation du rayon a de l'univers avec le temps t, une loi que l'on déduit des équations d'Einstein sous la forme paramétrique très simple suivante :

La signification physique du paramètre angulaire η sera donnée à la . Précisons tout de suite que la forme de ces équations correspond au cas où la contribution de la matière domine le contenu total en masse-énergie de l'univers, la densité de rayonnement pouvant alors être ignorée. On parle d'un univers « dominé par la matière ».

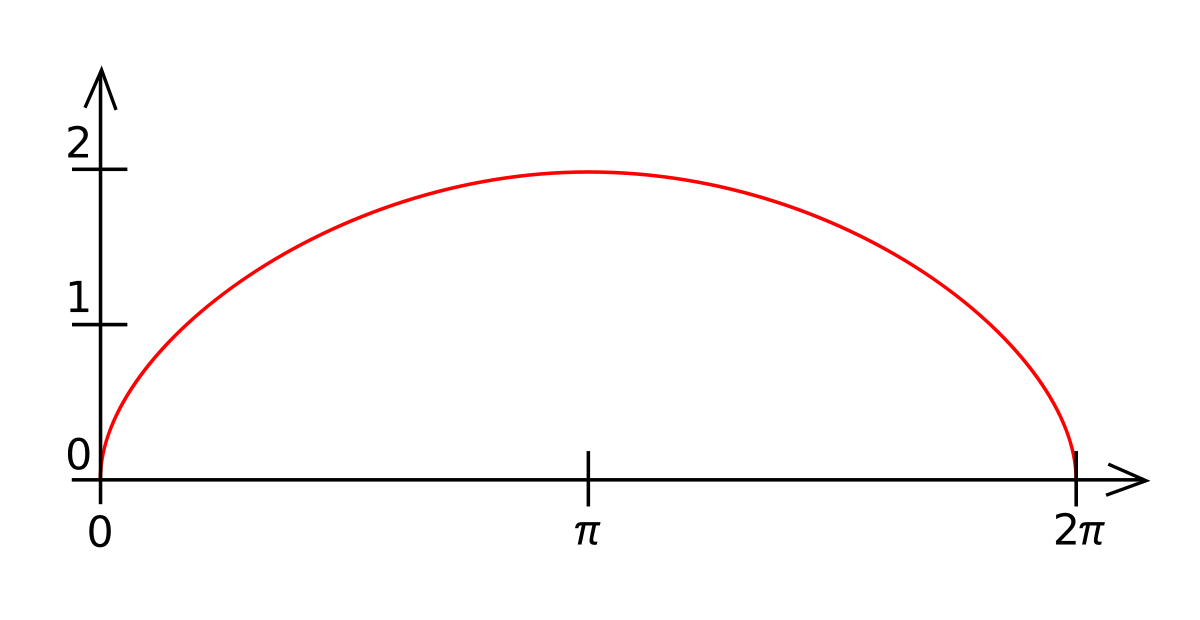
La courbe exprimant a en fonction de t s'appelle une cycloïde. C'est la courbe engendrée par le point d'un cercle de rayon A roulant sans glisser sur un axe et dont l'angle de rotation η augmente progressivement. On voit que le rayon a part de zéro, passe par un maximum égal au paramètre A pour η = π et revient de façon symétrique à la valeur 0 pour η = 2π. Ainsi cet univers de Friedmann subit successivement expansion puis contraction. Autrement dit il va du Big Bang au Big Crunch en passant par une phase d'expansion maximale. Après l'anéantissement de l'univers de Friedmann au Big Crunch, il n'y a aucun sens à parler de cycles postérieurs d'expansion-contraction car à l'effondrement ultime le temps lui-même disparaît (dans le modèle d'Einstein le temps est partie constitutive de l'univers et il n'existe donc pas de temps absolu pouvant servir de référence extérieure). C'est à proprement parler la fin des temps.

On voit sur les équations que le paramètre A représente le rayon de l'univers dans sa phase d'expansion maximale. Il est remarquable que ce paramètre caractérise entièrement l'univers et en détermine l'évolution. C'est dire son importance. Nous verrons plus loin que A mesure aussi (en unités convenables) la masse totale de l'univers. Notons que la durée de vie totale d'un univers de Friedmann de masse A, obtenue en prenant η = 2π dans l'équation donnant t, est

Il atteint son expansion maximale à l'âge πA / 2.

On remarque encore que la vitesse d'expansion d'un univers de Friedmann diminue avec le temps. L'expansion est décélérée (symétriquement la contraction est accélérée). On calcule facilement le terme d'accélération à partir des équations paramétriques sous la forme: