Algèbre universelle - Définition

Produits d'algèbres

Produits d'algèbres

Les notions de produit (direct) d'algèbres de groupes, d'anneaux et de modules se généralisent dans le cadre général de l'algèbre universelle.

Soit une famille d'algèbres de signature Ω indexée par un ensemble (fini ou non) et P le produit des ensemble sous-jacents à ces algèbres.

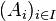
Définition. Il existe une unique structure algébrique de signature Ω sur P telle que, tout entier naturel n et pour tout élément ω de Ω_n, ω_A(x₁, ..., x_n) = pour tout élément x_k = de P, avec k = 1, ..., n. On dit que l'algèbre qu'est P muni de cette structure algébrique est le produit direct ou le produit ou l' algèbre produit. de cette famille d'algèbres. On la note . Si I = {1, ..., n}, la note aussi A₁ × ... × A_n.

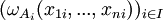
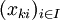
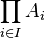
Exemple. Prenons le cas de deux algèbres A et B. Alors, la structure d'algèbre de A × B est définie de la manière suivante : pour tout entier naturel n, pour tout élément ω de Ω_n, quels que soient les éléments a_i de A_i et b_i de B_i, avec i = 1, ..., n, on a ((a₁, b₁), ..., (a_n, b_n)) = (ω_A(a₁, ..., a_n), (ω_B(b₁, ..., b_n).

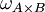
Voici quelques propriétés élémentaires des produits d'algèbres.

• Les projecteurs canoniques de . (qui à un élément associent sa composante d'indice donné) sont des homomorphismes surjectifs.
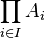
• La structure algébrique de est l'unique structure algébrique sur l'ensemble pour laquelle les projecteurs canoniques sont des homomorphismes.
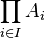
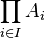
• Soit, pour tout i dans I, f_i un homomorphisme d'une algèbre A_i dans une algèbre B_i. Alors l'application de dans qui à associe est un homomorphisme.
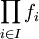
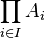
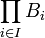
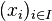
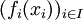
• Soit, pour tout i dans I, B_i une sous-algèbre de B_i. Alors est une sous-algèbre de .
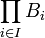
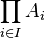
• Le produit d'algèbres est associatif et commutatif, en un sens à préciser que le lecteur pourra déterminer (de manière analogue au produit cartésien d'ensembles).
• Le graphe d'un homomorphisme entre deux algèbres A et B est une sous-algèbre de A × B.

Voici la propriété fondamentale des produits d'algèbres.

Théorème. Soient, pour tout i dans I, p_i le projecteur canonique du produit (à un élément on associe sa composante d'indice i) et soit B une algèbre. Quels que soient les homomorphismes f_i de B dans A_i (pour tout i dans I), il existe un unique homomorphisme g de B dans tel que, pour tout i dans I, (c'est l'homomorphisme dont les composantes sont les f_i).

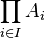
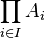
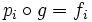
Le produit défini correspond au produit en termes de théorie des catégories.

Algèbre des applications

Soient A une algèbre et X un ensemble. L'ensemble des applications de X dans A s'identifie au produit A^X d'algèbres toutes égales à A. Il s'ensuit donc qu'il existe une structure algébrique canonique sur l'ensemble des applications de X dans A. Plusieurs exemples d'algèbres sont des sous-algèbres de des algèbres des applications d'un ensemble dans une algèbre.

Exemple. Soit E un espace topologique (un intervalle du corps R des nombres réels, par exemple). L'ensemble des fonctions de E dans R, ou dans le corps C des nombres complexes, est un anneau, et l'ensemble des fonctions continues de E dans R, ou C, est un sous-anneau de cet anneau. Si on note V un espace vectoriel réel ou complexe de dimension finie, l'ensemble des applications de E dans V est un espace vectoriel réel ou complexe et l'ensemble des applications continues de E dans V est un sous-espace vectoriel de cet espace vectoriel. On retrouve d'algèbres de ce type en analyse (anneaux ou espaces vectoriels d'applications continues, différentiables, analytiques, espace vectoriel d'applications intégrables, etc.).

Voici quelques propriétés de l'algèbre des applications.

• L'application diagonale de A dans A^X (qui à un élément de A associe l'application constante correspondante) est un homomorphisme.
• Pour tout élément x de X, l'évaluation en x, qui à une application de X dans A associe sa valeur x, est un homomorphisme de A^X dans A (c'est projecteur du produit).
• Pour toute partie Y de X, l'application de A^X dans A^Y qui à une application de X dans A associe sa restriction à Y est un homomorphisme.

Soient A et B des algèbres. L'ensemble des homomorphismes de A dans B n'est pas nécessairement une sous-algèbre de l'algèbre des applications de A dans B. Toutefois, c'est le cas pour les monoïdes commutatifs, les groupes commutatifs, les modules sur un anneau commutatif, mais pas pour les anneaux.