Algèbre universelle - Définition

Algèbre des termes et variétés d'algèbres

Algèbres des termes

L'algèbre des termes de signature Ω sur un ensemble est une algèbre qui va permettre de définir la notion d'identité dans une algèbre, par exemple l'associativité, la commutativité et la distributivité. Intuitivement, elle est formée de toutes les combinaisons formelles d'éléments de cet ensemble à partir d'éléments de Ω, interprétés comme des opérateurs. On peut penser à cette algèbre comme une sorte d'algèbre de polynômes en des indéterminées (en nombre fini ou infini).

Définition. Soit I un ensemble. Il existe un plus petit ensemble T tel que I et Ω₀ sont inclus dans T (on suppose ces deux ensembles disjoints) et tel que, pour tout entier naturel non nul n, pour tout élément ω de Ω_n et quels que soient les n éléments x₁, ..., x_n de T, la suite (ω,x₁, ..., x_n) appartient à T. Il existe alors une unique structure algébrique de signature Ω sur T telle que Ω₀ est l'ensemble des constantes de T et telle que, pour tout entier naturel non nul n, pour tout élément ω de Ω_n et quels que soient les n éléments x₁, ..., x_n de T, ω_T(x₁, ..., x_n) = (ω,x₁, ..., x_n), ce qui permet de désigner par ω(x₁, ..., x_n) l'élément (ω,x₁, ..., x_n) de T. On appelle algèbre des termes de signature Ω construite sur I et on note T_Ω(I) ou T(I) l'algèbre ainsi obtenue. On l'appelle aussi algèbres des mots ou algèbre absolument libre. On appelle termes ou mots les éléments de T.

L'élément i de T est noté X_i et les X_i sont appelées indéterminées de T.

Ainsi, les termes sont expressions formelles en faisant opérer les éléments de Ω sur les indéterminées (les X_i, éléments de I) et les constantes (les éléments de Ω₀), et en faisant opérer les éléments de Ω sur les expressions ainsi obtenues et réitérant le précédé, un nombre fini de fois.

Théorème. L'algèbre T = T_Ω(I) a une propriété universelle : pour toute algèbre A et pour toute application f de l'ensemble I dans A, il existe un unique homomorphisme d'algèbres de T dans A qui prolonge f, et on obtient ainsi une bijection entre l'ensemble des applications de I dans A et l'ensemble des homomorphismes de T sur dans A.

Soit A une algèbre. En identifiant l'ensemble des applications de I dans A à l'ensemble des familles d'éléments de A indexées par I, on a, d'après ce qui précède, une bijection canonique φ entre l'ensemble des familles d'éléments de A indexées par I et l'ensemble des homomorphismes de T dans A. Pour toute famille d'éléments de A indexée par I et pour tout élément t de T, on note note la valeur en t de l'homomorphisme φ() de T dans A : on dit alors que cet élément de A est obtenu en substitutant les a_i aux X_i. De manière intuitive, on remplace chaque occurrence de l'indéterminée X_i dans le terme t par l'élément a_i de A et on calcule l'expression obtenue dans A. Cela s'interprète de la même manière que la substitution aux indéterminées d'un polynôme d'élément d'une algèbre unifère associative commutatif sur un anneau commutatif.

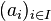
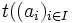
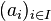
Pour toute algèbre A, il existe un homomorphisme surjectif à valeurs dans A définie sur l'algèbre des termes construits sur A.

Identités

Définition. On appelle identité de signature Ω construite sur X tout couple d'éléments de T = T_Ω(X). Étant donné un identité (u, v), on dit qu'une algèbre A satisfait l'identité u = v si, pour toute famille x = d'éléments de A indexée par I, on a u(x) = v(x), autrement dit, en substituant, pour tout élément i de I, un même élément de A à l'indéterminée X_i dans u et v, les éléments de A ainsi obtenus sont égaux.

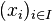
Exemples. On considère un magma M, c'est-à-dire un ensemble muni d'une seule loi de composition.

• On suppose que I = {1, 2, 3} et on considère T = T({1, 2, 3}) et l'identité(x₁x₂)x₃ = x₁(x₂x₃). Dire que M satisfait cette identité, c'est dire que M est associatif.
• On suppose que I = {1, 2} et on considère T = T({1, 2}) et l'identité x₁x₂ = x₂x₁. Dire que M satisfait cette identité, c'est dire que M est commutatif. Cet exemple s'applique aussi aux monoïdes, aux groupes et aux anneaux.

Exemples. Voici quelques exemples d'identités :

• associativité d'une loi de composition;
• commutativité d'une loi de composition;
• idempotence d'une loi de composition (le carré de tout élément x est égal à x), par exemple les lois d'un treillis;
• distributivité d'une loi de composition sur une autre (la multiplication par rapport à l'addition d'un anneau);
• distributivité d'une loi de composition externe sur une loi de composition (un des axiomes par exemple d'espace vectoriel ;
• l'« associativité » d'une loi externe (par exemple l'identité (ab)x = a(bx), dans un espace vectoriel sur un corps, où a et b sont des scalaires et x est un vecteur);
• le fait qu'un élément soit un élément neutre pour une loi de composition (quand l'élément neutre fait partie de la signature);
• le fait qu'un élément soit « neutre » pour une loi externe, (par exemple, l'identité 1.x = x dans un espace vectoriel sur un corps, où 1 est l'élément unité du corps des scalaires);
• le fait qu'une application donnée associe à tout élément d'un groupe son inverse (quand la fonction inverse fait partie de la signature).

Variétés d'algèbres

Définition. Une variété d'algèbres de signature Ω est une classe V d'algèbres de signature Ω telle qu'il existe un ensemble I et une partie S de T_Ω(I)× T_Ω(I) telle que V est la classe de toutes les algèbres de signature Ω qui satisfont chacune des identités de S. En fait, on pourrait, pour définir les variétés d'algèbres en général, se limiter à considérer l'algèbre des termes d'un ensemble infini dénombrable fixé une fois pour toute (l'ensemble des entiers naturels, par exemple).

Par exemple, les monoïdes, les groupes, les anneaux, les modules sur un anneau donné (ou espaces vectoriels sur un corps donné) forment des variétés d'algèbres.

Les variétés d'algèbres de signature donnée forment des catégories pour les homomorphismes et la composition des homomorphismes, et ces catégories ont la plupart des propriétés communes usuelles des catégories des groupes, des monoïdes, des anneaux, des espaces vectoriels sur un corps, etc. : construction des structures induites et des quotients, existence et construction des produits, existence d'objets libres, existence des limites et des colimites quelconques, construction des limites quelconques et des colimites filtrantes. En un sens, on peut dire que les variétés d'algèbres sont de « bonnes » catégories d'algèbres.

La classe de toutes les algèbres qui sont vides ou triviales forment une variété d'algèbres.

Certaines opérations de structures algébriques qui font que l'on a à faire à une variété d'algèbres ne sont pas données dans la définition usuelle. Par exemple, un groupe un ensemble muni d'une loi de composition vérifiant certaines propriétés, mais seules l'existence de l'élément neutre et l'existence de l'inverse de tout élément font partie de la définition usuelle, mais le groupe n'est pas, dans la définition usuelle, muni d'un élément neutre et d'une inversion. Pour déterminer les opérations qui dont que l'on a à faire à une variété d'algèbres, on peut examiner les axiomes des sous-structures (sous-groupes, sous-anneaux, etc.).

Soit V une variété d'algèbres. On a un foncteur, dit d' oubli, de la catégorie V dans la catégorie des ensembles en associant à toute algèbre A de V son ensemble sous-jacent.

Exemples de variétés d'algèbres

On trouvera ici la liste des principales variétés d'algèbres que l'on rencontre en mathématiques. Pour chacune des types de structure algébrique suivantes, la classe de toutes les algèbres qui sont de ce type forment une variété d'algèbres :

• Les ensembles (avec aucune opération finitaire).
• Les ensembles pointés, c'est-à-dire les ensembles munis d'un élément.
• Les magmas, c'est-à-dire les ensembles munis d'une loi de composition.
• Les magmas associatifs, c'est-à-dire les magmas dont loi est associative.
• Les magmas commutatifs, c'est-à-dire les magmas dont la loi est commutative.
• Les magmas unitaires, c'est-à-dire les magmas ayant un élément unité.
• Les monoïdes, c'est-à-dire les magmas unitaires dont la loi est associative.
• Les monoïdes commutatifs.
• Les groupes.
• Les groupes commutatifs.
• Les algèbres unaires à opérateurs dans un ensemble donné S, c'est-à-dire les ensembles E muni d'un loi externe de S sur E (donc un opérateur unaire sur E pour chacun des éléments de S).
• Les M-ensembles, où M est un monoïde donné (un groupe par exemple), c'est-à-dire les ensembles E munis d'une action de G sur E.
• Les groupes à opérateurs dans un ensemble donné S, c'est-à-dire les groupes G muni de loi externe de S sur G qui définie, pour chacun des éléments de S un endomorphisme de groupes de G.
• Les groupes commutatifs à opérateurs dans un ensemble donné S.
• Les quasigroupes.
• Les boucles. Les boucles associatives ne sont autres que les groupes.
• Les semi-anneaux.
• Les anneaux.
• Les anneaux commutatifs.
• Les modules sur un anneau donné A (en particulier, les espaces vectoriels sur un corps donné K).
• Les bimodules sur deux anneaux donnés A et B (une opération unaire pour chacun des éléments de A et de B).
• Les algèbres sur un anneau commutatif donné A (sans hypothèses sur la multiplication autre que la bilinéarité).
• Les algèbres associatives sur un anneau commutatif donné A.
• Les algèbres unitaires associatives sur un anneau commutatif donné A.
• Les algèbres unitaires associatives commutatives un anneau commutatif donné A.
• Les algèbres alternatives sur un anneau commutatif donné A, c'est-à-dire une algèbre sur A dont la multiplication est telle que (xx)y = x(xy) et y(xx) = (yx)x quels que soient les éléments x et y de A (par exemple, l'algèbre réelle des octonions de Cayley).
• Les algèbres alternatives unitaires sur un anneau commutatif donné A.
• Les anneaux involutifs, c'est-à-dire les anneaux A muni d'un antiautomorphisme d'anneau de A (un isomorphisme de A sur l'anneau opposé à A). Exemples : le corps des nombres complexes muni de la conjugaison des nombres complexes ou le corps des quaternions muni de la conjugaison des quaternions. Ils servent dans la théorie des formes sesquilinéaires sur un anneau.
• Les algèbres involutives sur un anneau involutif commutatif donné A (le corps des nombres complexes pour la conjugaison, par exemple), c'est-à-dire les algèbres associatives E sur A muni d'un endomorphisme de groupes de x → x* de E qui est semi-linéaire pour l'involution de A qui est tel que (x*)* = x et (xy)* = y*x* quels que soient x et y dans E. On rencontre les algèbres involutives complexes en analyse fonctionnelle (C*-algèbres).
• Les algèbres involutives unitaires sur un anneau involutif commutatif donné A.
• Les modules différentiels sur un anneau commutatif donné A, c'est-à-dire les A-modules M muni d'un endomorphisme D de M tel que D(D(x)) = 0 pour tout élément x dans M. On rencontre les modules involutifs en algèbre homologique (un complexes de chaînes peut être considéré comme un module différentiel).
• Les anneaux différentiels, c'est-à-dire les anneaux A muni d'un endomorphisme de groupe D de A tel que, quels que soient les éléments x et y dans A, on ait D(xy) = D(x).y + x.D(y). Exemple : l'anneau des polynômes à une indéterminé à coefficients dans un anneau muni de la dérivation des polynômes, ou encore l'anneau des fonctions réelles indéfiniment différentiables définies sur R muni de la dérivation de ses fonctions.
• Les algèbres de Lie sur un anneau commutatif donné A.
• Les algèbres de Jordan sur un corps commutatif K de caractéristique différente de 2.
• Les semi-treillis ou demi-treillis, c'est-à-dire les magmas associatifs commutatifs T tels que, pour tout élément x de T, x² = x.
• Les treillis.
• Les treillis bornés, c'est-à-dire les treillis ayant un plus petit élément et un plus grand élément, ces éléments ayant considéré comme des opérations nullaires.
• Les treillis distributifs.
• Les treillis modulaires.
• Les algèbres de Boole.
• Les anneaux booléens, c'est-à-dire les anneaux A tel que, pour tout élément x de A, x² = x. Il est équivalent de se donner une structure d'algèbre de Boole sur un ensemble et une structure d'anneau booléen sur cet ensemble.

Voici des structures algébriques qui ne forment pas des variétés d'algèbres : les semi-groupes, c'est-à-dire les monoïdes dont tout élément est simplifiable, les corps, les anneaux principaux, les anneaux factoriels, les modules libres sur un anneau donné non trivial A qui n'est pas un corps, les treillis complets.

Soit K un corps (commutatif ou non). Soit X un espace affine sur un corps K, en considérant l'ensemble vide comme un espace affine attaché à un espace vectoriel nul. Alors, pour tout entier naturel non nul n et pour toute suite finie de n éléments de K dont la somme est égale à 1, on a opération n-aire qui à une suite de n-points associe le barycentre de ces points affecté de ces éléments de K. On définit donc une structure algébrique sur X. En fait, on peut montrer, que, en associant à chaque espace affine sur K l'algèbre ainsi définie, on a un foncteur de la catégorie des espaces affines sur K (les morphismes sont les applications affines) dans une variété d'algèbres qui est en fait une équivalence de catégories. Ceci montre que les propriétés catégorielles des variétés d'algèbres s'appliquent à la catégorie des espaces affine sur K.

Propriétés des variétés d'algèbres

Les variétés d'algèbres sont stables pour la plupart des constructions usuelles en algèbre. Soit V une variété d'algèbres. On a les propriétés suivantes.

• Tout sous-algèbre d'une algèbre de V est une algèbre de V.
• Pour toute congruence R d'une algèbre A de V, l'algèbre quotient de A par R est une algèbre de V.
• Quelles que soient les algèbres A et B, s'il existe un homomorphisme surjectif de A sur B et si A est une algèbre de V, alors B est une algèbre de V.
• Toute algèbre qui est isomorphe à une algèbre de V est une algèbre de V.
• L'algèbre produit d'une famille d'algèbres de V est une algèbre de V.
• L'algèbre vide (s'il en existe) est une algèbre de V et toute algèbre triviale (c'est-à-dire qui est un singleton) est une algèbre de V.

En fait, on a la caractérisation suivante des variétés d'algèbres.

Théorème de Birkhoff. Pour qu'une classe V d'algèbres de signature Ω soit une variété d'algèbres, il faut et il suffit qu'elle vérifie les propriétés suivantes :

• toute sous-algèbre d'une algèbre de V est une algèbre de V;
• quelles que soient les algèbres A et B, si A est une algèbre de V et s'il existe un homomorphisme surjectif de A sur B, alors B est une algèbre de V;
• le produit d'une famille d'algèbres de V est une algèbre de V.

Proposition. Soit V une variété d'algèbres. Alors, au sens de la théorie des catégories, les isomorphismes de la catégorie V ne sont autres que les homomorphismes de V qui sont des bijections et les monomorphismes de V ne sont autres que les homomorphismes de V qui sont des injections. Tout homomorphisme surjectif de V est un épimorphisme de la catégorie V, mais la réciproque peut être fausse, comme le montre la catégorie des anneaux (ou des monoïdes) : on peut montrer qu'il existe, dans la catégorie des anneaux, l'injection canonique de l'anneau Z des entiers rationnels dans le corps Q des nombres rationnels est un épimorphisme.

Dans les variétés d'algèbres, certains auteurs appellent épimorphismes les homomorphismes surjectifs, ce qui peut créer une confusion avec les épimorphisme de la théorie des catégories.

Proposition. Le produits directs d'algèbres de V ne sont autres que les produits au sens de la théorie des catégories.

Toutes les propriétés générales des variétés d'algèbres s'appliquent à toutes les structures algébriques qui forment des variétés d'algèbres énumérées précédemment, et à bien d'autres. On peut donc définir pour ses structures des homomorphismes, des sous-algèbres et les congruences, et on peut construites les produits directs et les quotients, et ce, de manière uniforme. De plus, comme on le verra, on peut construire les limites quelconques et les colimites filtrantes de foncteurs (en particulier des limites projectives et inductives de systèmes projectifs et systèmes inductif indexés par des ensembles ordonnés filtrants) de la même manière qu'en théorie des ensembles. En particulier on a des égalisateurs, des coégalisateurs et des produits fibrés, construits comme en théorie des ensembles. On peut aussi montrer que ces structures admettent des colimites quelconques, et en particulier des coproduits (ou sommes) et des coproduits fibrés (ou sommes amalgamées ou fibrées), mais chaque variété d'algèbres à sa construction, qui peut différer de la construction que l'on retrouve en théorie des ensembles. On peut construire les algèbres libres engendrées par des ensembles.