Algèbre universelle - Définition

Limites et colimites

Soit V une variété d'algèbres de signature Ω. On peut montrer que la catégorie V admet des limites projectives et des limites inductives, et même, plus généralement, des limites et des colimites. On peut aussi montrer que le foncteur d'oubli de V dans la catégorie des ensembles crée les limites quelconques et crée les colimites filtrantes (les limites inductives filtrantes).

Théorème. Soient I une petite catégorie (resp. un ensemble ordonné filtrant) et F un foncteur de I dans V et considérons L la limite (resp. la colimite) de F considéré comme foncteur dans la catégorie des ensembles, au moyen du foncteur d'oubli. Alors il existe une unique structure algébrique de signature Ω sur L pour laquelle, pour tout élément i de I, l'application canonique de L dans F_i (resp. de L dans F_i) est un homomorphisme. Alors, pour cette structure algébrique sur L, L est, pour les applications canoniques, une limite (resp. une colimite) du foncteur F dans la catégorie V. On peut montrer que cette construction est fonctorielle.

En particulier, on peut remplacer I par un ensemble ordonné (resp. un ensemble ordonné filtrant) et F par un système projectif (resp. un système inductif) d'algèbres de V : on obtient les limites projectives (resp. les limites inductives).

Exemples (tous construits comme dans la catégorie des ensembles)

• Les produit d'algèbres de V.
• L'égalisateur et le coégalisateur de deux homomorphismes entre deux algèbres A et B.
• Le produits fibré d'algèbres de A et B de V relativement à des homomorphismes u et v d'une algèbre S à valeurs dans A et B respectivement.

La catégorie V admet des limites et des colimites quelconques, et donc la catégorie est complète et cocomplète. Cela tomberait en défaut si on n'admettait les algèbres (s'il en existait du moins).

Coproduits et coproduits fibrés. Cela a pour conséquence que les variétés d'algèbres admettent des coproduits (ou sommes directes). Voici des exemples de coproduits :

• pour les familles de groupes (ou les monoïdes), les coproduits sont les produits libres;
• pour les familles de modules sur un même anneau (ou les groupes commutatifs), les coproduits sont les sommes directes;
• pour les familles finies d'algèbres unitaires associatives commutatives sur un même anneau commutatif, les coproduits sont les produits tensoriels (de même pour les anneaux commutatifs).

Comme on le voit, les coproduits sont rarement construits comme dans le cas des ensembles (c'est alors la réunion disjointe).

Les variétés d'algèbres admettent aussi des coproduits fibrés (ou sommes amalgamées).

Algèbres libres

Algèbres libres

On retrouve en algèbre différents objets libres sur un ensemble : les monoïdes libres, les groupes libres, les modules libres sur un anneau donné, les algèbres de polynômes à coefficients dans un anneau commutatif. Tous ces exemples sont assez bien connus (au niveau universitaire). Toutes ces constructions ont des propriétés communes, qui en fait relève de la théorie des catégories, et se généralisent dans les variétés d'algèbres.

Soit V une variété d'algèbre de signature Ω, et on suppose qu'il existe des algèbres non triviales dans V, c'est-à-dire qui ont plus d'un élément. Alors on a le théorème suivant :

Théorème. Pour tout ensemble I, il existe une algèbre L de V qui contient I comme sous-ensemble telle que, pour toute algèbre A de V et pour toute application f de I dans A, il existe un unique homomorphisme de L dans A qui prolonge f. On dit qu'une telle algèbre L est une algèbre libre construite sur I dans V. La partie I de L est alors une partie génératrice de L.

Si V est la variété de toutes les algèbres de signature Ω, alors l'algèbre de termes T_Ω(I) est une algèbre libre construite sur I.

Proposition. Quelles que soient les algèbres libres L et M construites sur I dans V, il existe un unique isomorphisme de L sur M qui prolonge l'application identité de l'ensemble I. Ainsi, l'algèbre libre construite sur I dans V est unique à un isomorphisme unique près.

Les algèbres libres construites sur I dans V sont donc uniques à un isomorphisme unique près. On peut donc en choisir une fois pour toute. Mais il y a une construction canonique, qui est une algèbre quotient de l'algèbre des termes construits sur I. Cette construction est valable dans chacune des variétés d'algèbres, mais en pratique, dans les variétés d'algèbres les plus importantes, il y a une construit explicite plus simple, qui dépend réellement de la variété d'algèbres considérée. La construction explicite n'a pas vraiment d'importance, mais on en construit une pour pouvoir parler de l' algèbre libre et non pas d'une algèbre libre construite sur I. Voici sa construction.

Soit S l'ensemble des couples d'éléments de T_Ω(N) (N est l'ensemble des entiers naturels) qui sont des identités satisfaites par toute algèbre de V et soit R la congruence de T_Ω(I) engendrée par l'ensemble des (f(s), f(t)) tels que f est un homomorphisme de T_Ω(N) dans T_Ω(I) et (s, t) est un élément de S. Alors la composée de l'injection canonique de I dans T_Ω(I) et de la surjection canonique de T_Ω(I) sur L = T_Ω(I)/R est une injection et, en identifiant I à l'image de cette injection, L est une algèbre libre construite sur I dans V, que l'on l'appelle l' algèbre libre construite sur I dans V et on la note L_V(I).

Exemples. Voici des variétés d'algèbres où la construction explicite des algèbres libres construites une ensemble I est bien connue, avec une indication de la construction explicite :

• les magmas : c'est en fait l'algèbre des termes;
• les monoïdes : le monoïde des mots construits sur I, c'est-à-dire l'ensemble des suites finies d'éléments de I, avec pour produit la juxtaposition (et avec le mot vide comme élément neutre);
• les groupes : le groupe libre construit sur I;
• les monoïdes commutatifs : l'ensemble des familles à support fini d'éléments de N indexée par l'ensemble I;
• les modules sur un anneau donné A : l'ensemble des familles à support fini d'éléments de A indexée par l'ensemble I;
• les algèbres unitaires associatives sur un anneau commutatif donné A : l'algèbre tensorielle sur le A-module libre construit sur I;
• les algèbres unitaires associatives commutative sur un anneau commutatif donné A : l'algèbre des polynômes à coefficients dans A avec une indéterminée par chacun des éléments de I, qui est isomorphe à l'algèbre symétrique du A-module libre construit sur I.

Proposition. Quels que soient les ensembles I et J et l'application f de I dans J, il existe un unique homomorphisme de L_V(I) dans L_V(J) qui prolonge f, et on le note L_V(f). Cet homomorphisme est injectif, surjectif ou un isomorphisme suivant que f est injective, surjectif et bijective. En termes de la théorie des catégories, on définit ainsi un foncteur F de la catégorie des ensembles dans V, qui est en fait un adjoint à gauche du foncteur d'oubli de V dans la catégorie des ensembles.

Définition. On dit qu'une algèbre de V est libre en tant qu'algèbre de V (sans référence à un ensemble d'indéterminées) si elle est isomorphe une algèbre libre construite sur un ensemble dans V. Cela dépend de la variété V et non pas seulement de Ω. Cela généralise la notion de module libre ou de groupe libre.

Pour toute algèbre A, il existe un homomorphisme surjectif à valeurs dans A définie sur une algèbre libre construite sur l'ensemble sous-jacent à A.

Algèbres initiales

Au sens de la théorie des catégories, toute variété d'algèbres A admet des objets initiaux, c'est-à-dire une algèbre U telle que, pour toute algèbre de A de V, il existe un unique homomorphisme de U dans A. Les objets initiaux dans la variété V ne sont autres que objets libres construits sur l'ensemble vide, et ils sont uniques à un isomorphisme unique près.

Dans la catégorie des ensembles, l'ensemble vide est l'unique objet initial, mais dans une variété d'algèbres, les objets initiaux n'ont pas comme ensemble sous-jacent l'ensemble vide, sauf s'il n'y a aucune opération nullaire dans la signature (alors que les objets finaux ont comme ensemble sous-jacent les singletons, objets finaux de la catégorie des ensembles).

Voici quelques exemples d'objets initiaux dans des variétés d'algèbres :

• pour les magmas ou les magmas associatifs, le magma vide est l'unique objet initial;
• pour les ensembles pointés, les monoïdes, les groupes et les modules sur un anneau donné, les objets initiaux sont les algèbres triviales;
• pour les anneaux, l'anneau Z des entiers rationnels en est un objet initial;
• pour tout anneau commutatif K, K est un objet initial de la variété des algèbres unifères associatives sur K;
• le treillis vide est l'unique objet initial de la variété des treillis;
• l'algèbre de Boole {0, 1} est un objet initial de la variété des algèbres de Boole.

Algèbres libres sur un ensemble à un élément

Le foncteur d'oubli de la variété d'algèbres V dans la catégorie des ensembles est représentable. Autrement dit, il existe un couple (U, c) formé d'une algèbre U de V et d'un élément c de V tel que, pour toute algèbre A de V, l'application f → f(c) de Hom(U, A) dans l'ensemble sous-jacent à A est bijection. Les représentants de foncteur s'identifient aux algèbres libres construites sur un ensemble à un élément (le c en question) dans V. Dans la catégorie des ensembles, le couple ({0}, 0) est un représentant du foncteur identité de la catégorie des ensembles.

Voici quelques exemples dans dans variétés d'algèbres:

• pour la catégorie des monoïdes (et des monoïdes commutatifs): (N, 1), où N est monoïde additif des entiers naturels (incluant 0);
• pour les magmas associatifs (et des magmas associatifs commutatifs): (N \ {0}, 1), en considérant l'addition;
• pour les groupes (et groupes commutatifs): (Z, 1);
• pour les A-modules, où A est un anneau: (A, 1);
• pour les M-ensembles, où M un monoïde (c'est les ensembles E munis d'un action de M sur E): (M, 1);
• pour les K-algèbres unitaires associatives (et commutatives), le couple (K[X], X), K désigne la K-algèbre des polynômes à une indéterminée X;
• pour les ensembles pointés: (({0, 1}, 0), 1).

Soit G un groupe. Pour qu'une action de G sur un ensemble non vide E soit simplement transitive, il faut et il suffit que le G-ensemble qu'est l'ensemble E muni de cette action soit un G-ensemble libre construite sur un élément de E.

Substitution

Soit I un ensemble. Pour tout élément i de I, on peut alors noter X_i l'élément de L_V(I) auquel s'identifie i, et on dit que les X_i sont des indéterminées de L_V(I). En interprétant ainsi les éléments de I, on a le résultat qui suit.

Soit A une algèbre de V. En identifiant l'ensemble des applications de I dans A à l'ensemble des familles d'éléments de A indexées par I, on a, d'après la définition des algèbres libres, une bijection canonique φ entre l'ensemble des familles d'éléments de A indexées par I et l'ensemble des homomorphismes de L = L_V(I) dans A. Pour toute famille d'éléments de A indexée par I et pour tout élément t de L, on note la valeur en t de φ(): on dit alors que cet élément de A est obtenu en substituant les x_i aux X_i. Cela s'interprète de la même manière que la substitution aux indéterminées d'un polynôme d'élément d'une algèbre unitaire associative commutative sur un anneau commutatif.

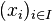
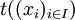
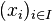
Soit A une algèbre de V, t un élément de L = L_V(I). En associant de cette manière à tout élément de A^I un élément d'élément de A, obtenue par substitution dans t, on obtient une application de A^I dans A qui s'interprète, dans la cas de la variété des algèbres unitaires associatives commutatives sur un anneau commutatif K, comme l'application polynomiale associée à t.

Dépendance et bases

Soient A une algèbre de V, une famille d'éléments de A indexée par un ensemble I et φ l'homomorphisme correspondant de L_V(I) dans A.

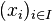
• Pour que cette famille soit une famille génératrice de A, il faut et il suffit que φ soit une surjection, ce qui ne dépend que de la signature d'algèbres, et non pas de la variété d'algèbres.
• On dit que cette famille est libre ou que ses éléments sont indépendants dans A si φ est une injection, et sinon on dit que la famille est liée ou que ses éléments dépendants. Cela généralise la notion de dépendance linéaire que l'on rencontre en algèbre linéaire et de dépendance algébrique que l'on rencontre dans les algèbres unitaires associatives commutatives sur un anneau commutatif (algèbre des polynômes).
• On dit qu'une famille d'éléments de A est une base de A si elle est une famille génératrice et une famille libre, c'est-à-dire si φ est un isomorphisme. Cela généralise les bases des modules ou des espaces vectoriels.
• L'algèbre A est libre dans V si et seulement si elle admet une base relativement à V.

Les notions de famille libre, d'éléments indépendants et de base dépendent de la variété d'algèbres et non seulement de la signature d'algèbres, contrairement au cas des familles génératrices.

Présentations

On retrouve en algèbre les présentations de groupes. Cette notion se généralise au cas des variétés d'algèbres.

Définition. Soit A une algèbre de la variété d'algèbre V. On appelle présentation de A (relativement à V) tout couple (X, S) formé d'une partie génératrice X de A et d'un ensemble S de couples d'éléments l'algèbre libre L construite sur X telle que la congruence R d'algèbre de L engendrée par S est la relation d'équivalence associée à l'unique homomorphisme de L sur A qui prolonge l'injection canonique de X dans A. Les éléments de X sont alors appelés générateurs de la présentation et les éléments de S les relations de la présentation.

Cette notion de présentations dans une variété d'algèbres généralise bien celle des groupes. Dans le cas des groupes, on se donne une partie génératrice X d'un groupe G (les générateurs) et un partie K du groupe libre L construit sur X (les relateurs) telle que le sous-groupe distingué de L engendré par K est le noyau de l'unique homomorphisme de L dans G qui prolonge l'injection canonique de X dans G. Le passage de la partie K à l'ensemble S de couples de L se fait ainsi : au lieu de considéré un élément x de L (un relateur de la présentation), on considère le couple (x, e) formé de x et de l'élément neutre e de L (une relation de al présentation).

Toute algèbre A d'une variété d'algèbre V admet une présentation.

La notion de présentation d'algèbres permet parfois de faire plus simplement certains calculs, en particulier lorsque l'on considère toutes la variété de toutes les algèbres d'une signature donnée ou encore lorsque l'on peut construite explicitement les algèbres libres dans la variété en question (par exemple la catégorie des groupes).

On dit qu'une algèbre A de V est de présentation finie s'il existe une présentation (X, S) de A telle que les ensembles X et S sont finis.

Si une algèbre A de V est de présentation finie, alors elle est de type fini.