Anneau factoriel - Définition

Exemples et contre-exemples

• L'anneau Z est un exemple simple d'anneau factoriel. Un autre exemple est l'anneau de Gauss Z[i] des complexes s'écrivant sous la forme a + ib où a et b sont des entiers relatifs.
• Si K est un corps alors l'ensemble K[X] des polynômes à coefficient dans K est un anneau factoriel, ainsi que K[X₁, X₂, ...,X_n]. Plus généralement, dès que A est factoriel, il en est de même de A[X].
• On démontre que tout anneau principal (à plus forte raison tout anneau euclidien) est aussi factoriel
• Le contre-exemple le plus célèbre est l'anneau non-factoriel dans lequel on trouve deux décompositions différentes de 4 : . Propriété qui donna l'occasion à Leonhard Euler de présenter une démonstration fausse du dernier théorème de Fermat pour n = 3 (Algebra 1770). Pour pallier cette difficulté, la méthode la plus simple est d'utiliser les entiers d'Eisenstein. La configuration générale d'une situation de cette nature est étudiée dans l'article sur les entiers quadratiques. Pour trouver une solution très générale à cette difficulté Ernst Kummer crée des nombres idéaux, maintenant formalisé par les travaux de Richard Dedekind à travers le concept d'anneau de Dedekind.
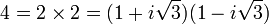
• Un contre-exemple "géométrique" est celui du quotient de K[X,Y,Z] par l'idéal engendré par X² − YZ.

Soit p l'application de passage au quotient. p(X²) admet deux décompositions distinctes en facteurs irréductibles : on a p(X²) = p(X)p(X) mais aussi p(X²) = p(Y)p(Z)

Motivation

L'arithmétique dans l'anneau des entiers relatifs permet la démonstration de nombreux théorèmes. Les démonstrations utilisent le fait que cet anneau est euclidien donc principal. En revanche, de nombreux anneaux ne le sont pas, par exemple celui des polynômes à coefficients dans les entiers relatifs ou encore les polynômes en plusieurs indéterminées sur un corps commutatif.

Ce dernier exemple est important, les variétés algébriques sont définies comme les racines d'un idéal de polynômes à plusieurs variables. Ainsi la sphère réelle est définie comme les racines communes des polynômes à trois indéterminées multiples de X² + Y² + Z² - 1. L'anneau des fonctions polynomiales définies sur la sphère n'est ni euclidien ni principal. En revanche, il est factoriel.

Sur un anneau factoriel, certains théorèmes fondamentaux des anneaux principaux restent vrais. Ainsi, le lemme d'Euclide, les propriétés des plus petits communs multiples et des plus grands communs diviseur ou encore le théorème fondamental de l'arithmétique restent valables (ce dernier est vérifié par définition).

Tous ne s'appliquent plus, ainsi un idéal premier n'est pas toujours maximal. Dans Z[X], l'anneau des polynômes à coefficients dans l'anneau Z des entiers relatifs, l'idéal 2Z[X] n'est pas maximal et Z[X] / 2Z[X] n'est pas un corps car la classe de X n'est pas inversible. L'identité de Bézout n'est pas toujours vérifiée : dans Z[X] les éléments 2 et X n'ont pas de facteur commun, pourtant l'idéal engendré par 2 et X n'est pas l'anneau tout entier.

Propriétés

Premières propriétés

• Un anneau commutatif unitaire et intègre est factoriel si et seulement s'il vérifie les deux propriétés suivantes :

(1) Toute suite croissante d'idéaux principaux est stationnaire.

(2) Tout idéal engendré par un élément irréductible est premier.

Cette caractéristique est parfois plus simple pour établir le caractère factoriel d'un anneau. La proposition suivante en est un exemple :

• Tout anneau principal est factoriel.

En effet, un anneau principal est noethérien, la première propriété est ainsi vérifiée. De plus si p est irréductible, l'idéal des multiples de p est premier et maximal. Ces propriétés sont démontrées dans l'article Anneau principal.

• Tout anneau factoriel est intégralement clos.

La démonstration est identique à celle présentée dans l'article Anneau principal. Rappelons que A est dit intégralement clos si les seuls éléments de son corps des fractions qui sont entiers sur A (c'est-à-dire racines d'un polynôme unitaire à coefficients dans A) sont les éléments de A.

• Soit π un élément irréductible de A ; si π divise le produit de deux éléments a et b, alors il divise a ou b.

Ce résultat est connu sous le nom de lemme d'Euclide ou parfois lemme de Gauss. Il est la conséquence directe de l'unicité de la décomposition de a.b en facteurs irréductibles.

• Si A vérifie les deux propriétés ci-dessous alors il est factoriel :

(1) Toute suite croissante d'idéaux principaux est stationnaire.

(2) Tout idéal engendré par un élément irréductible est premier.

En vue de montrer cette implication, une décomposition de la démonstration est utile. Soient A un anneau vérifiant les hypothèses de la première définition et a un élément de A, non nul et non inversible.

• Il existe un élément irréductible qui divise a :

On construit par récurrence une suite (a_n) de la manière suivante: a₀ est égal à a, supposons la suite définie jusqu'à l'ordre n – 1; si a_n-1 est irréductible alors a_n est égal à a_{n - 1}, sinon a_n est un diviseur strict de a_{n - 1}. L'élément b de A est dit diviseur strict de a_{n - 1} s'il n'est pas inversible et s'il existe un élément c de A non inversible tel que b.c soit égal à a_{n - 1}.

La suite des idéaux principaux (a_nA) est croissante, la première partie de la définition indique qu'elle est stationnaire à partir d'un certain rang, noté ici m. Le fait que la suite soit stationnaire montre que a_m est irréductible. Par construction, il divise a.

• Il existe une suite finie p₁, …, p_n d'éléments irréductibles tels que :

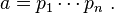
Si a est irréductible, la proposition est évidente : on prend n = 1 et p₁ = a. Sinon, le résultat précédent montre l'existence d'un élément irréductible p₁ et d'un élément u₁ non inversible tels que a = p₁.u₁. Si u₁ est irréductible, la proposition est démontrée ; s'il ne l'est pas, il existe un élément p₂ irréductible et un élément u₂ non inversible tels que a = p₁.p₂.u₂. En réitérant le raisonnement on trouve soit un élément u_n irréductible et la proposition est démontrée, soit une suite infinie (u_i). La suite des idéaux (u_iA) est alors strictement croissante, ce qui est impossible. Cette impossibilité démontre la proposition.

• La décomposition en facteurs irréductibles est unique :

On suppose l'existence de deux décompositions :

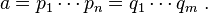
Montrons la proposition par récurrence sur n. Si n = 1 alors a est irréductible, m est aussi égal à 1 et la proposition est démontrée.

Supposons la proposition démontrée à l'ordre n – 1, et montrons-la à l'ordre n. L'élément p_n divise le produit q₁ …q_m, on en déduit que l'idéal p_nA contient q₁ …q_m. Comme cet idéal est premier, il contient l'un des q_k ; ce q _k est donc un multiple de p_n. Comme l'élément q _k est irréductible, il existe un élément inversible u tel que p_n = u.q _k.

L'égalité suivante et l'hypothèse de récurrence permettent de conclure :

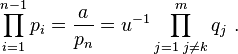
• Si l'anneau est factoriel alors il vérifie les propriétés (1) et (2) :

Soit σ la fonction de A – {0} dans l'ensemble N des entiers naturels qui à a associe le nombre de facteurs non inversibles dans la décomposition en facteurs irréductibles de a. L'unicité de la décomposition dans un anneau factoriel montre que la fonction σ est bien définie.

Soit a et b deux éléments non nuls de A. L'unicité de la décomposition montre aussi que σ(a.b) = σ(a) + σ(b). Ainsi si c divise strictement a, alors σ(a) est strictement plus grand que σ(c).

• Toute suite croissante d'idéaux principaux est stationnaire :

Soit (a_nA) une suite croissante d'idéaux principaux. Si la suite des (a_n) est constante égal à zéro, la suite est stationnaire. Sinon, quitte à réindexer la suite, supposons que a₁ ne soit pas nul. Dire que l'idéal a_{n + 1}A contient strictement l'idéal a_nA signifie que a_{n + 1} divise strictement a_n. Cela ne peut arriver que pour un nombre fini (inférieur ou égal à σ(a₁)) d'entiers n, ce qui montre que la suite est constante à partir d'un certain rang, c'est-à-dire stationnaire.

• Soit p un élément irréductible de A, l'idéal pA est premier :

Soient a et b deux éléments de A tels que ab est élément de pA. Alors ab étant un multiple de p, la décomposition en facteurs irréductibles de ab contient nécessairement p à un facteur inversible près. En conséquence soit la décomposition de a soit celle de b contient p, à un facteur inversible près. Ce qui montre que soit a soit b est élément de l'idéal pA. Cette propriété traduit le fait que l'idéal est premier et termine la démonstration.

Diviseur et multiple communs

Soit (a_n) une famille d'éléments non nuls de A.

• Le plus grand commun diviseur de ces éléments est, parmi les diviseurs communs aux a_n, celui qui est multiple de tous les autres. Il est unique à produit près par un inversible : c'est le produit de tous les irréductibles p_i présents dans la décomposition en facteurs irréductibles de chaque a_n, affectés chacun d'un exposant égal au plus petit de ses ordres de multiplicité dans les a_n.

• Le plus petit commun multiple des a_n est, parmi les multiples communs (s'il en existe) à ces éléments, celui qui est diviseur de tous les autres. Il est unique à produit près par un inversible s'il existe (ce qui est toujours le cas si l'ensemble des a_n est fini) : c'est le produit des facteurs p_i présents dans la décomposition en facteurs irréductibles d'au moins l'un des a_n, affectés chacun d'un exposant égal au plus grand de ses ordres de multiplicité dans les a_n.

• Les a_n sont dits premiers entre eux, ou premiers entre eux dans leur ensemble, si leur plus grand diviseur commun est égal à un. Ils sont dits premiers entre eux deux à deux si pour toute paire {m,n} d'indices, a_m et a_n sont premiers entre eux.

Ces définitions généralisent les notions de plus petit commun multiple et plus grand commun diviseur. Dans ce contexte, certaines des propriétés vraies sur un anneau principal s'appliquent encore, d'autres non. La relation d'ordre partiel utilisée ici (ou plus exactement : de préordre partiel) est la divisibilité : a est plus petit que b si c'est un diviseur de b. Elle se traduit en termes d'idéaux par l'ordre inverse de l'inclusion : a est plus petit que b si l'idéal engendré par a contient l'idéal engendré par b.

Soient (a_n) une famille d'éléments non nuls de A et a, b deux éléments non nuls de A.

• Il existe un élément inversible u tel que

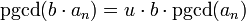
• Si la famille (a_n) est finie, il existe un élément inversible u tel que

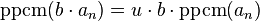
• Si la famille (a_n) est finie et si les a_n sont premiers entre eux deux à deux, il existe un élément inversible u tel que

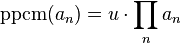
• Il existe un élément inversible u tel que

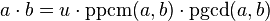
• Le plus petit idéal principal contenant tous les a_n est l'idéal engendré par le plus grand commun diviseur des a_n.

En effet, il suffit de remarquer qu'un idéal principal, engendré par un élément d, contient tous les a_n si et seulement si d divise tous les a_n, c'est-à-dire divise leur plus grand commun diviseur, autrement dit si cet idéal contient celui engendré par le plus grand commun diviseur. Ce plus petit idéal principal contenant tous les a_n contient l'idéal engendré par la famille, mais lorsque ce dernier n'est pas principal, l'inclusion est stricte. Ainsi dans Z[X], l'idéal engendré par 2 et X est l'ensemble des polynômes dont le terme constant est pair, mais le plus petit idéal principal le contenant est l'anneau entier. Dans un anneau principal, les deux idéaux sont égaux. Ce résultat est connu sous le nom de théorème de Bachet-Bézout.

• Si les a_n admettent un plus petit commun multiple, l'intersection des idéaux engendrés par les a_n est l'idéal principal engendré par ce plus petit commun multiple.

• Si R désigne la relation d'équivalence d'association définie dans le paragraphe Définitions et A* l'ensemble des éléments non nuls de l'anneau, alors l'ensemble quotient A*/R des classes d'association, muni des opérateurs pgcd et ppcm, forme un treillis.

Anneau des polynômes

Les anneaux de polynômes représentent la première motivation historique pour les anneaux factoriels. Si les coefficients sont choisi dans un corps commutatif, l'anneau dispose d'une division euclidienne, dans le cas contraire une autre arithmétique apparaît. En 1801 Carl Friedrich Gauss publie un traité dans lequel il montre que l'anneau des polynômes à coefficients entiers possède un propriété qui se traduit, en terme moderne, par le fait que cet anneau est factoriel. Une présentation moins générale est proposée dans l'article lemme de Gauss.

Dans ce paragraphe A désigne un anneau factoriel et K son corps des fractions. Il est utile, pour étudier les polynômes à coefficients dans A, d'expliciter deux définitions :

• Un polynôme de A[X] est dit primitif si et seulement si les coefficients du polynôme sont premiers entre eux dans leur ensemble.

• Le contenu d'un polynôme P non nul à coefficients dans K est un élément a de K tel qu'il existe un polynôme primitif Q de A[X] tel que aQ soit égal à P. Dans cet article, on note cont(P) le contenu de P:

Parmi les propriétés suivantes, les deux premières donnent un sens à cette définition du contenu :

• Tout polynôme non nul à coefficients dans A (resp. K) possède un contenu appartenant à A (resp. K).

• Le contenu d'un polynôme est unique à produit près par un élément inversible de A.

• Soient P et Q deux polynômes non nuls à coefficients dans K, l'égalité suivante est vérifiée, à produit près par un élément inversible de A :

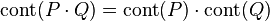
Le résultat suivant est connu sous le nom de lemme de Gauss dans le cas où A est l'anneau Z des entiers relatifs :

• Un polynôme non constant à coefficients dans A est irréductible dans A[X] si et seulement s'il est primitif dans A[X] et irréductible dans K[X].

On en déduit le corollaire suivant :

• Pour tout entier naturel n, l'anneau de polynômes en n indéterminées A[X₁, ..., X_n] est factoriel.

• Tout polynôme P non nul à coefficients dans A (resp. K) possède un contenu appartenant à A (resp. K) :

Si P est à coefficients dans A, il suffit de poser cont(P) = le pgcd de ses coefficients : le quotient de P par cet élément de A sera bien primitif. Si maintenant les coefficients de P sont seulement dans K, c'est-à-dire sont des fractions d'éléments de A, on se ramène au cas précédent en réduisant ces fractions à un dénominateur commun b (par exemple le produit de leurs dénominateurs respectifs) : P s'écrit R / b avec b élément non nul de A et R polynôme à coefficients dans A, auquel le début du raisonnement s'applique. De R = cont(R)Q avec Q primitif on déduit ainsi P = (cont(R) / b)Q, ce qui montre la proposition.

• Le contenu d'un polynôme non nul est unique à produit près par un élément inversible de A :

Si P est à coefficients dans A, son contenu ne peut être que le pgcd de ses coefficients. Il est donc déterminé de façon unique à produit près par un inversible. Si maintenant P = R / b avec les mêmes notations que précédemment, de P = cont(P)Q on déduit R = b.cont(P)Q donc cont(R) = b.cont(P), si bien que le contenu de P, égal au quotient par b de celui de R, est, comme lui, déterminé de façon unique à produit près par un inversible.

• Soient P et Q deux polynômes non nuls à coefficients dans K, l'égalité suivante est vérifiée, à produit près par un élément inversible de A :

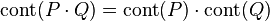
Par définition du contenu, il suffit de montrer l'égalité pour deux polynômes à coefficients dans A et primitifs. Pour cela raisonnons par contraposée : montrons que si P.Q n'est pas primitif alors P ou Q n'est pas primitif. Si P.Q n'est pas primitif, il existe un élément irréductible p qui divise chacun des coefficients. Soit J un idéal maximal contenant p et φ le morphisme canonique de l'anneau A[X] dans (A / pA)[X]. Par hypothèse p divise chacun des coefficients de P.Q, on en déduit que φ(P.Q) est nul, autrement dit, que φ(P).φ(Q) est nul. Comme A / pA est un corps, φ(P), ou φ(Q) est nul, ce qui revient à dire que p divise le contenu de P ou de Q. La contraposée indique que si P et Q sont primitifs, alors P.Q l'est aussi.

• Soit P un polynôme non constant à coefficients dans A. Le polynôme est irréductible dans A[X] si et seulement s'il est primitif dans A[X] et irréductible dans K[X] :

Il s'agit de prouver que si P est irréductible dans A[X] alors il est primitif, et que si P est primitif alors son irréductibilité (ou sa réductibilité) dans A[X] équivaut à celle dans K[X].

Supposons P irréductible dans A[X] et observons la décomposition P = cont(P)Q : les deux facteurs sont dans A[X], donc l'un des deux doit être inversible, or ce ne peut pas être Q (qui est de même degré que P). Par conséquent cont(P) est inversible dans A[X] donc dans A, si bien que P est primitif.

Supposons maintenant P primitif et montrons qu'il est réductible dans K[X] si et seulement s'il l'est dans A[X]. Si P est réductible dans K[X] alors il existe deux polynômes B et C dans K[X], non nuls et non inversibles, donc non constants, tels que P = B.C. La proposition précédente montre l'existence dans A[X] de deux polynômes Q et R de mêmes degrés respectifs que B et C, donc non inversibles, tels que :

, si bien que P est réductible dans A[X]. Réciproquement, si P est réductible dans A[X], c'est-à-dire produit de deux éléments non inversibles de A[X] alors (comme P est primitif) les deux facteurs sont non constants, donc non inversibles dans K[X], si bien que P est réductible dans K[X].

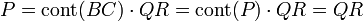
• L'anneau A[X] est factoriel :

La méthode usuelle, pour démontrer l'existence et l'"unicité" (à permutation et association près) de la décomposition d'un élément non nul P de A[X] en produit d'irréductibles, consiste à utiliser sa décomposition dans l'anneau K[X], dont on sait qu'il est factoriel (et même euclidien).

Soit P = P₁ ... P_m une décomposition de P en produit d'éléments irréductibles P_i de K[X]. Pour chaque indice i, notons c_i "le" contenu (à produit près par une unité de A) de P_i, et Q_i le polynôme primitif P_i / c_i. D'après la proposition précédente, les Q_i sont irréductibles dans A[X]. Or P = c Q₁ ... Q_m, en notant c le produit des c_i. Cet élément c est égal au contenu de P, donc il appartient à A. Notons alors c = p₁ ... p_n "sa" décomposition en irréductibles dans A. On obtient une décomposition de P en produit d'irréductibles de A[X] : P = p₁ ... p_nQ₁ ... Q_m.

Si P = r₁ ... r_n'S₁ ... S_m' en est une autre (en distinguant de même parmi les facteurs, par des notations différentes, polynômes constants et non constants) alors, par "unicité" de la décomposition de P dans K[X], m' = m et (quitte à réordonner les S_i) S_i = u_iQ_i où u_i est a priori dans K, mais est en fait égal au contenu de S_i, donc est un élément inversible de A. Par élimination, les deux produits p₁ ... p_n et r₁ ... r_n' sont donc associés dans A. Par factorialité de A, ils ont alors (même nombre de facteurs, n' = n et) mêmes facteurs (à permutation et association près), ce qui termine la preuve d'unicité de la décomposition de P dans A[X].

• Soit n un entier naturel, l'anneau A[X₁, ..., X_n] est factoriel :

Cette proposition (immédiate pour n = 0 puisqu'il s'agit alors de l'anneau A) se déduit de la précédente par récurrence sur le nombre n d'indéterminées, en utilisant l'isomorphisme naturel d'anneaux entre A[X₁, ..., X_{n - 1}][X_n] et A[X₁, ..., X_n].