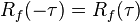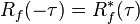Autocorrélation - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Applications
- La mesure du spectre optique et la mesure de flash lumineux de très courte durée produit par laser, en utilisant un autocorrélateur optique.
- En optique, l'autocorrélation normalisée et la corrélation croisée donnent le degré de cohérence d'un champ électromagnétique.
- En traitement du signal, l'autocorrélation peut donner une information sur des événements répétés tels que les battements musicaux ou les fréquences de pulsar, même si cela ne peut pas donner la position dans le temps du battement.
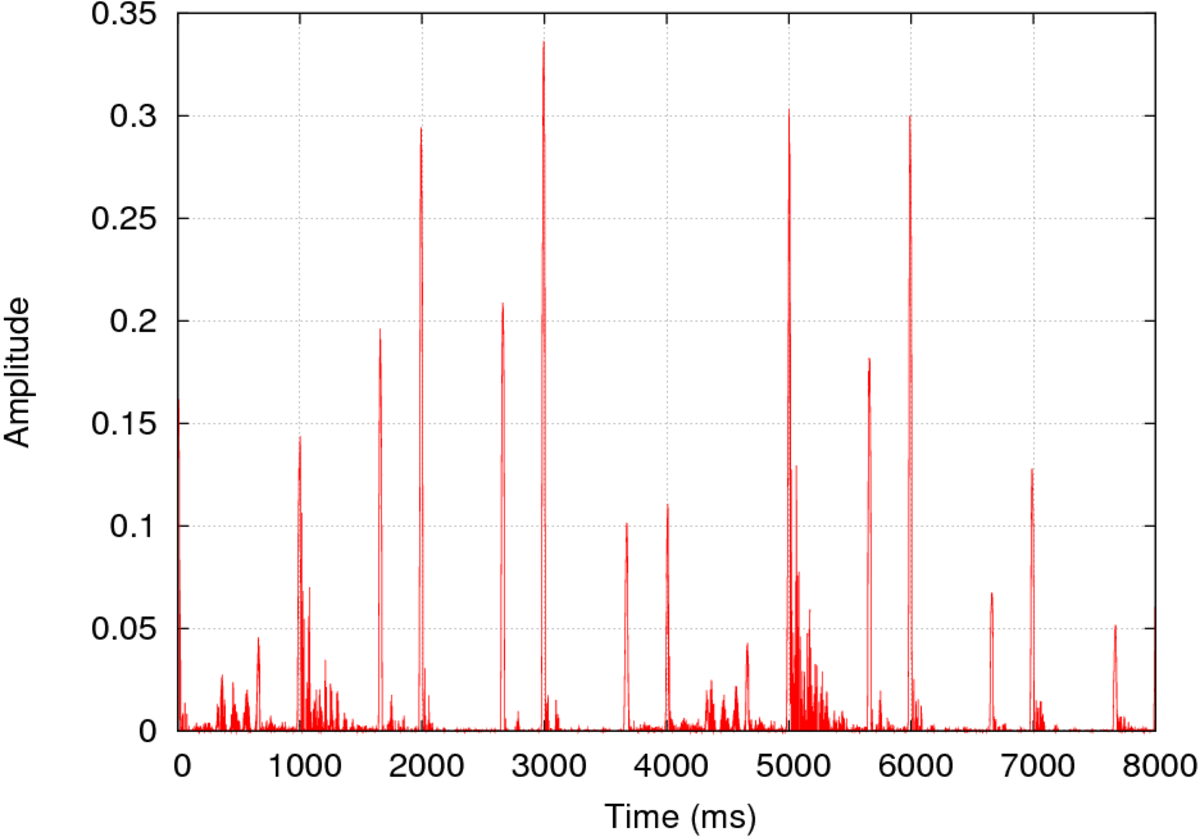
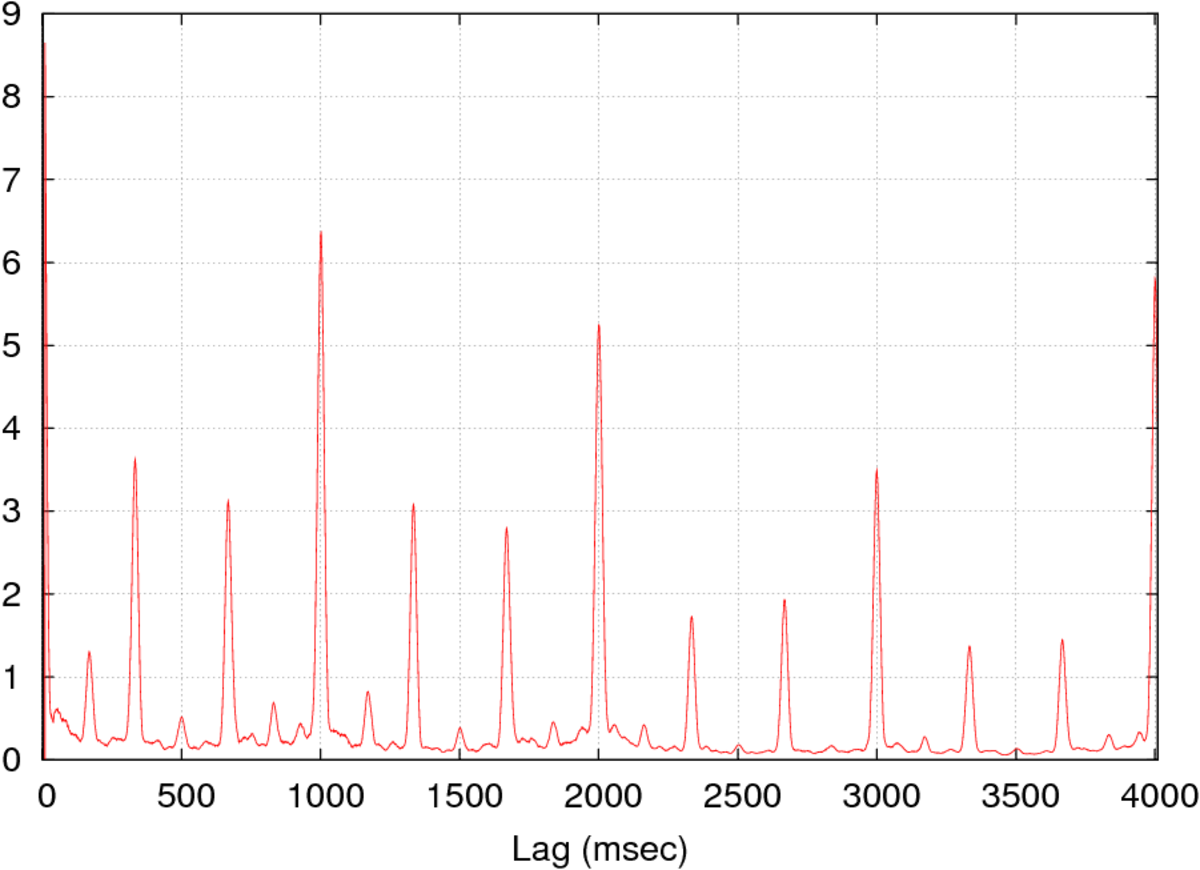
L'exemple suivant montre le signal d'un fichier sonore MIDI Le Beau Danube bleu (à gauche), et son autocorrélation (seulement les 4 premières secondes).
Signal original, Le Beau Danube bleu. | 
L'autocorrélation du signal (les quatre premières secondes). |
- L'autocorrélation, utilisée précédemment comme intermédiaire dans le calcul d'une densité spectrale, est aujourd'hui abandonnée au profit de la transformation de Fourier rapide (voir aussi Analyse spectrale pour des considérations élémentaires).
Propriétés
Dans ce qui suit, nous décrirons les propriétés d'autocorrélation uni-dimensionnelle uniquement, puisque la plupart des propriétés sont facilement étendues du cas à une dimension aux cas multidimensionnels.
- Une propriété fondamentale de l'autocorrélation est la symétrie, R(i) = R(−i), ce qui se démontre à partir de la définition. Dans un cas continu, l'autocorrélation est même une fonction paire
- quand f est une fonction réelle, et une fonction Hermitienne
- quand f est une fonction complexe.
- La fonction continue d'autocorrélation atteint son pic à l'origine, où elle prend une valeur réelle. C’est-à-dire que pour tout délai τ,
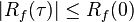
- L'autocorrélation d'une fonction périodique est, elle-même, périodique avec exactement la même période.
- L'autocorrélation de la somme de deux fonctions totalement non-corrélées (la corrélation croisée est zéro pour tout τ) est la somme des autocorrélations de chacune des fonctions.
- Puisque l'autocorrélation est un type spécifique de corrélation croisée, elle conserve toutes les propriétés de la corrélation croisée.
- L'autocorrélation d'un bruit blanc aura un pic important à τ = 0 et sera proche de 0 pour tout autre τ. Cela montre qu'un enregistrement de bruit blanc à un certain moment n'est pas corrélé statistiquement à un enregistrement du même bruit blanc à un autre moment.
- Le théorème de Wiener–Khintchine rapporte la fonction d'autocorrélation à la densité spectrale de puissance par la transformée de Fourier:
