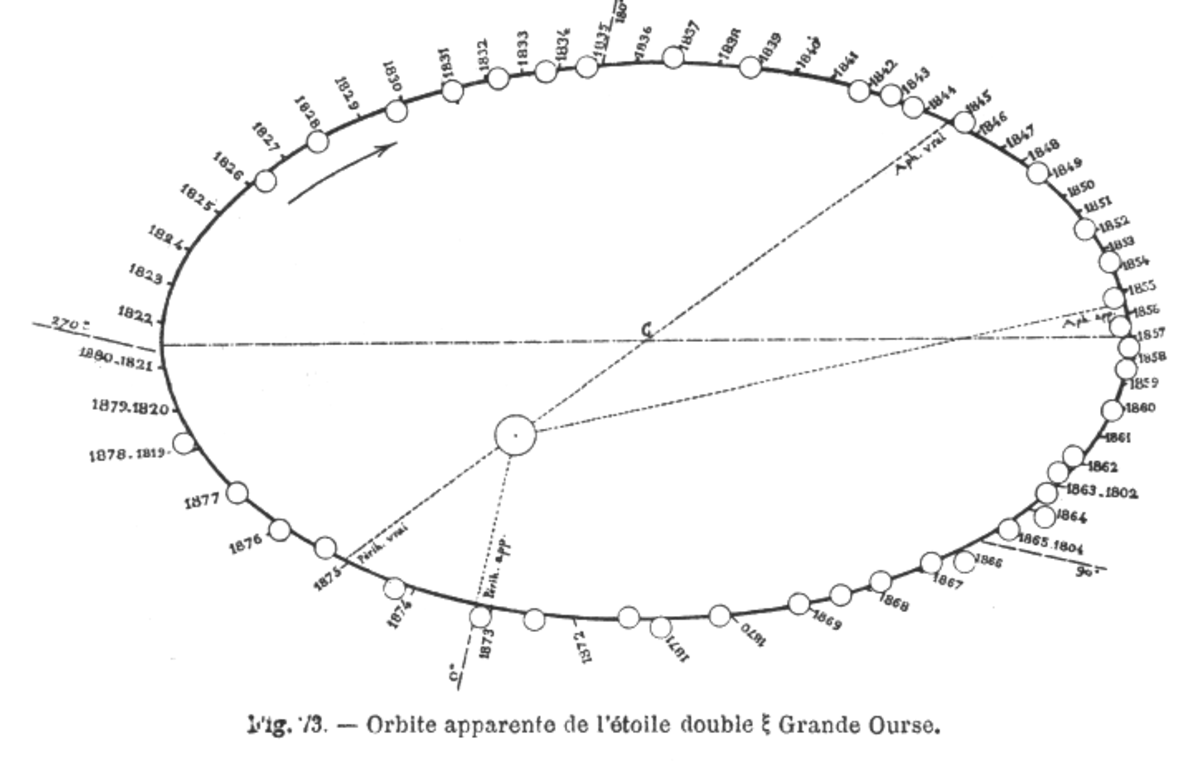
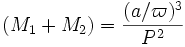Binaire visuelle - Définition

Théorie et application

Équations du mouvement

La trajectoire de l'étoile secondaire relativement à la primaire est une orbite homothétique de celle de chaque composante autour du centre de masse. On peut se rapporter aux binaires astrométriques où les équations du mouvement en coordonnées équatoriales sont décrites, à la différence près que l'angle entre la ligne des nœuds et le grand axe dans le plan de la vraie orbite se réfère ici à la secondaire, avec ω₂ = ω₁ + π, et que le demi-grand axe a est celui de l'orbite relative.

Cependant, et depuis les travaux d'Herschel (William), les positions relatives de la secondaire sont usuellement repérées en coordonnées polaires : la séparation ρ (en seconde d'arc) entre les composantes, et l'angle de position θ compté positivement à partir du Nord en direction de l'Est, depuis Herschel (John). Les données observées donnent ρ sin θ = -Δα cos δ et ρ cos θ = -Δδ, où Δα et Δδ sont les variations des coordonnées équatoriales dues au mouvement orbital seul, et dont on connaît l'expression en fonction des paramètres orbitaux.

Masses et luminosités

La troisième loi de Kepler modifiée par Newton s'écrit a³/P² = G M /(4 π²) où M est la masse totale du système, G la constante gravitationnelle, P la période, et a le demi-grand axe de l'orbite.

En unités physiques adaptées au problème des étoiles doubles, on a donc :

où:

• M₁ = masse de l'étoile primaire en masse solaire.
• M₂ = masse de l'objet secondaire en masse solaire.
• a₁ = demi-grand axe de l'orbite de la primaire autour du barycentre en seconde d'arc.
• a₂ = demi-grand axe de l'orbite de la secondaire autour du barycentre en seconde d'arc.
• a = a₁+a₂ = demi-grand axe de l'orbite relative en seconde d'arc.
• = parallaxe annuelle en seconde d'arc
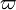
• P = période orbitale en années.

La connaissance de l'orbite (membre de droite) permet donc d'avoir accès à la somme des masses, le problème étant de connaître la parallaxe de l'étoile. Pour obtenir les masses individuelles, il faut que la binaire visuelle soit également :

• soit astrométrique, parce que l'orbite a été obtenue par astrométrie de façon absolue ou par rapport à d'autres étoiles de fond. L'orbite de chaque composante autour du barycentre est alors connue, donnant le rapport des masses, puisque a₁ M₁ = a₂ M₂. La parallaxe est généralement connue dans ce cas.
• soit binaire spectroscopique. Si elle est binaire à un spectre (BS1), l'inclinaison connue donne le demi-grand axe de la primaire en unité astronomique et il faut faire des hypothèses supplémentaires. Si c'est une binaire à deux spectres (BS2), le rapport de masse est obtenu, ainsi que les demi-grands axes en unité astronomique. Par le rapport entre le demi-grand axe du couple en unités angulaires et ce même demi-grand axe en unités linéaires, on obtient donc en prime ce qu'on appelle la parallaxe orbitale.

Faute de mieux, on peut s'aider d'une relation masse-luminosité, mais les masses obtenues ne sont alors plus purement orbitales.

Les magnitudes individuelles sont disponibles puisque le système est résolu, et les luminosités intrinsèques sont obtenues si la parallaxe est connue.

Classification

Il est clair que les étoiles doubles visuelles se répartissent en :

• couples optiques
• couples physiques

Cette dernière catégorie pouvant être également astrométrique, si les positions sur le ciel de chaque composante ont pu être mesurées précisément avec l'astrométrie (par exemple Hipparcos ou HST).

Dans ce qui suit, on ne s'intéressera qu'à celles dont l'orbite képlérienne peut être mise en évidence.

Orbite de ξ Ursae Majoris, d'après Camille Flammarion (1882)