Connexité par arcs - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus particulièrement en topologie, la connexité par arcs est un raffinement de la notion de connexité. Un espace topologique est dit connexe par arcs si deux points quelconques peuvent toujours être reliés par un chemin. En fait, la connexité est la notion fondamentale. Mais la connexité par arcs est plus intuitive, et se trouve être très souvent la meilleure façon de prouver la connexité.
Chemins
Avant de définir la connexité par arcs, il faut définir ce qu'on appelle « relier par un chemin ». Selon le cadre où l'on se trouve, on peut considérer des chemins particuliers.
Chemins dans un espace topologique
Si E est un espace topologique et si x et y sont deux points de E, on appelle chemin d'origine x et d'extrémité y toute application continue
![\gamma : [0,1] \rightarrow E](https://static.techno-science.net/illustration/Definitions/autres/3/36f47598cda2372b676519381c687d59_dad32cdaf2f30c773f4a46f1b2f8cf03.png)
On dit que x et y sont reliés si et seulement s’il existe un chemin d'origine x et d'extrémité y.
La relation « x est relié à y » est une relation d'équivalence sur E.
- x est relié à x, grâce au chemin constant γ(t) = x pour tout
![t \in [0,1]](https://static.techno-science.net/illustration/Definitions/autres/d/d9a06fde4663cdd5b1ba693e9127232f_ce76be6544934df881b7082a83aabd2d.png)
- si x est relié à y alors y est relié à x, grâce au chemin opposé
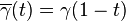
![t \in [0,1]](https://static.techno-science.net/illustration/Definitions/autres/d/d9a06fde4663cdd5b1ba693e9127232f_ce76be6544934df881b7082a83aabd2d.png)
- si x est relié à y et y est relié à z alors x est relié à z. En effet, si γ1 relie x à y et γ2 relie y à z alors le chemin composé
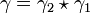
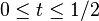
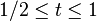
Chemins dans un espace vectoriel normé
Dans le cas où l'espace ambiant E est un espace vectoriel normé, on peut préciser la nature des chemins qui relient les points.
- Chemins rectilignes : un chemin est dit rectiligne si et seulement s'il peut s'écrire
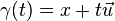
![t \in [0,1]](https://static.techno-science.net/illustration/Definitions/autres/d/d9a06fde4663cdd5b1ba693e9127232f_ce76be6544934df881b7082a83aabd2d.png)
- Chemins polygonaux : un chemin est dit polygonal si et seulement s’il s'écrit comme un composé d'un nombre fini de chemins rectilignes. Par exemple, un trajet dans Manhattan est un chemin polygonal.
- Chemins de classe
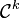
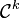
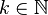
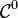
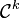
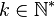
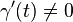
![t \in [0,1]](https://static.techno-science.net/illustration/Definitions/autres/d/d9a06fde4663cdd5b1ba693e9127232f_ce76be6544934df881b7082a83aabd2d.png)
Connexité par arcs
Ces différents types de chemins vont permettre de définir différents types de connexité par arcs selon les cas.
Définition
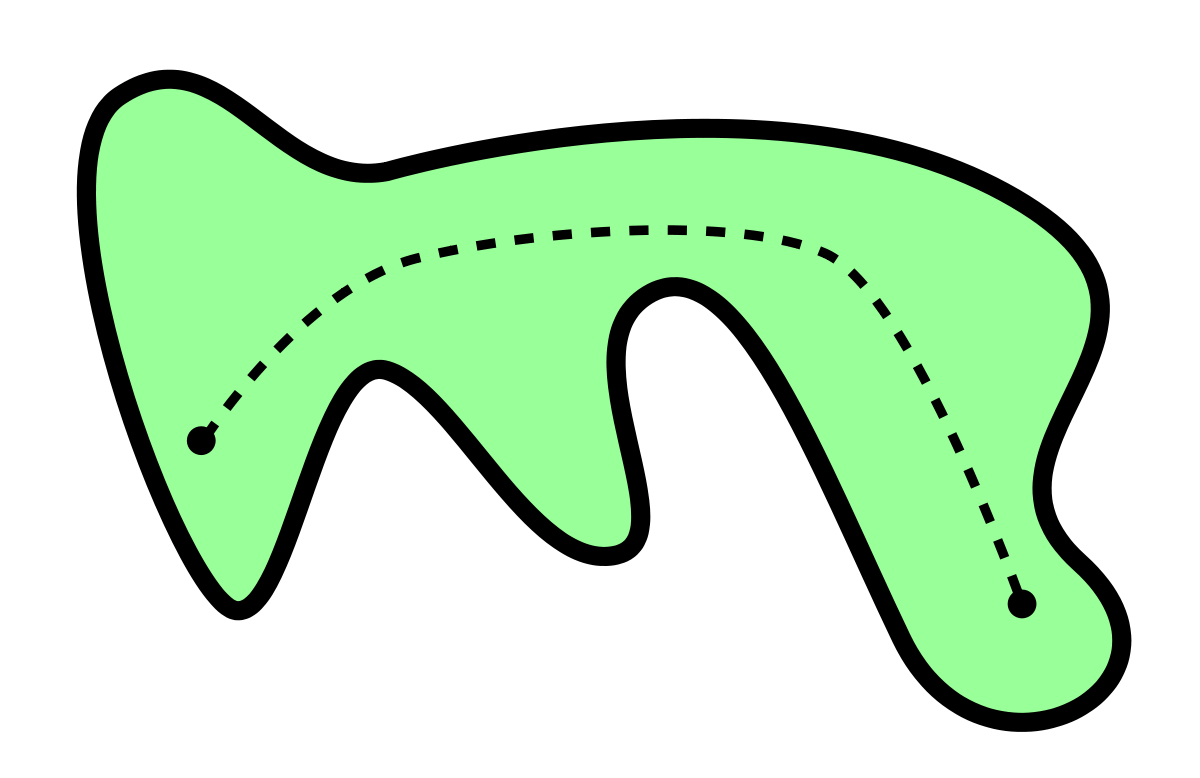
Un espace topologique E est dit connexe par arcs si et seulement si tout couple de points de E est relié par un chemin.
Une partie A de E est dite connexe par arcs si et seulement si tout couple de points de A est relié par un chemin restant dans A.
Une partie A d'un espace vectoriel normé est dite connexe par arcs polygonaux (respectivement par arcs
Lien avec la connexité
En apparence la connexité par arcs est très proche de la connexité ; on pourrait croire que « pouvoir toujours relier deux points » est équivalent à « être d'un seul tenant ». En fait on peut seulement affirmer : tout espace connexe par arcs est connexe.
La différence est subtile, et il est difficile d'exhiber un contre-exemple pour invalider la réciproque. Voici un contre-exemple classique. On définit une fonction f par
Cette fonction est continue sur ]0,1]. On note
![\Gamma = \{ (x,f(x)) | x \in ]0,1] \}](https://static.techno-science.net/illustration/Definitions/autres/b/b0653663df283f900c587cde5bd6439c_fc13973efcb944b36eccbe86428396b5.png)
![C = \overline{\Gamma} = \Gamma \cup \left( \{ 0 \} \times [-1,1] \right)](https://static.techno-science.net/illustration/Definitions/autres/d/d146bf772554879b119a07c0fbff2607_1a95e84b7b84fbda61f29941ec46f867.png)
Alors Γ est connexe comme graphe d'une fonction continue, C est connexe comme adhérence d'une partie connexe. Mais on peut montrer que C n'est pas connexe par arcs.
Cependant tout ouvert connexe d'un espace vectoriel normé est connexe par arcs.
Soit U un ouvert connexe d'un espace vectoriel topologique, x un point de U et V la composante connexe par arcs contenant x. V est non vide car il contient x. Soit y un point de V, il existe une boule B de rayon strictement positif et inclus dans U car U est ouvert. Tout point de B est connecté par arcs à y dans B. On en déduit que B est dans la composante connexe de y, donc de x, ce qui montre que B est inclus dans V et que V est ouvert.
Montrons que V est fermé. Soit z un élément de l'adhérence de V dans U. Il existe une boule B de rayon strictement positif et inclus dans U car U est ouvert. Comme zest élément de l'adhérence de V, il existe dans B un point y de V. Les points y et z sont dans la même composante connexe, car ils sont tout deux dans une boule incluse dans U. On en déduit que z est élément de V et que V est fermé.
L'ensemble V est non vide, ouvert et fermé, il est donc égal à U car U est connexe.
La démonstration précédente se généralise à tout ouvert connexe d'une variété topologique qui est donc connexe par arcs.
Lien avec la continuité
La connexité par arcs, comme la connexité, est conservée par les applications continues. Si E et F sont deux espaces topologiques, et si
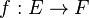
Si
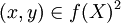
![\gamma : [0,1] \rightarrow X](https://static.techno-science.net/illustration/Definitions/autres/1/1c6d126f9daae8437b645ef36b11d045_2cb3e3410eb3a605f45ec06f4f911ba9.png)
![\gamma' = f \circ \gamma : [0,1] \rightarrow f(X)](https://static.techno-science.net/illustration/Definitions/autres/7/7ca024dd6190be104f95ee66b24de00b_68a90965e400a3c79c540166a1668754.png)
On a des résultats similaires pour les types plus spécifiques de connexités par arcs :
- la connexité par arcs polygonaux est conservée par les applications linéaires et par les applications affines ;
- la connexité par arcs
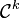
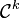
Produit
Soient E et F deux espaces topologiques connexes par arcs :
-
- Le produit cartésien ExF, munis de la la topologie produit, est connexe par arcs.
S'en persuader est chose aisée. Soit (x1, y1) et (x2, y2) deux points de ExF. La connexité par arcs de E et F montre l'existence de deux chemins γx et γy à valeurs dans E et F tels que : γx(0) = x1, γx(1) = x2, γy(0) = y1 et γy(1) = y2. Le chemin γ, qui à t, un nombre réel compris entre 0 et 1, associe (γx(t),γy(t)), montre la connexité par arcs de l'espace produit.
Exemples
- Dans un espace vectoriel normé, une partie convexe ou étoilée est connexe par arcs.
- Un cercle est connexe par arcs
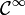
- Un carré est connexe par arcs polygonaux mais pas par arcs
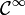
- Le plan privé des points à coordonnées rationnelles :
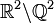
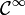
- Le groupe spécial orthogonal
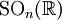
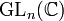
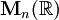
![\begin{array}{r|ccc}f : & ]0,1] & \longrightarrow & \R \\ & x & \longmapsto & \displaystyle \cos \left( \frac{1}{x} \right). \end{array}](https://static.techno-science.net/illustration/Definitions/autres/0/0e7b7b4a4bdaafbc685bfa9b9c14a2ac_5ad88030be57595c52ae3b85905c6b31.png)

















































