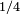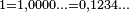Développement décimal de l'unité - Définition
La liste des auteurs de cet article est disponible ici.
Applications
Une application de
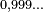
-
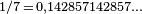
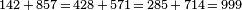
-
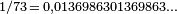
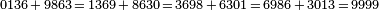
E. Midy a démontré en 1836 un résultat général sur ce genre de fractions, maintenant connu sous le nom de théorème de Midy. La publication était obscure, et il n'est pas clair si sa démonstration impliquait directement
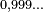
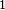
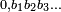
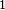
Pour retourner à l'analyse réelle, l'analogue en base

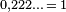
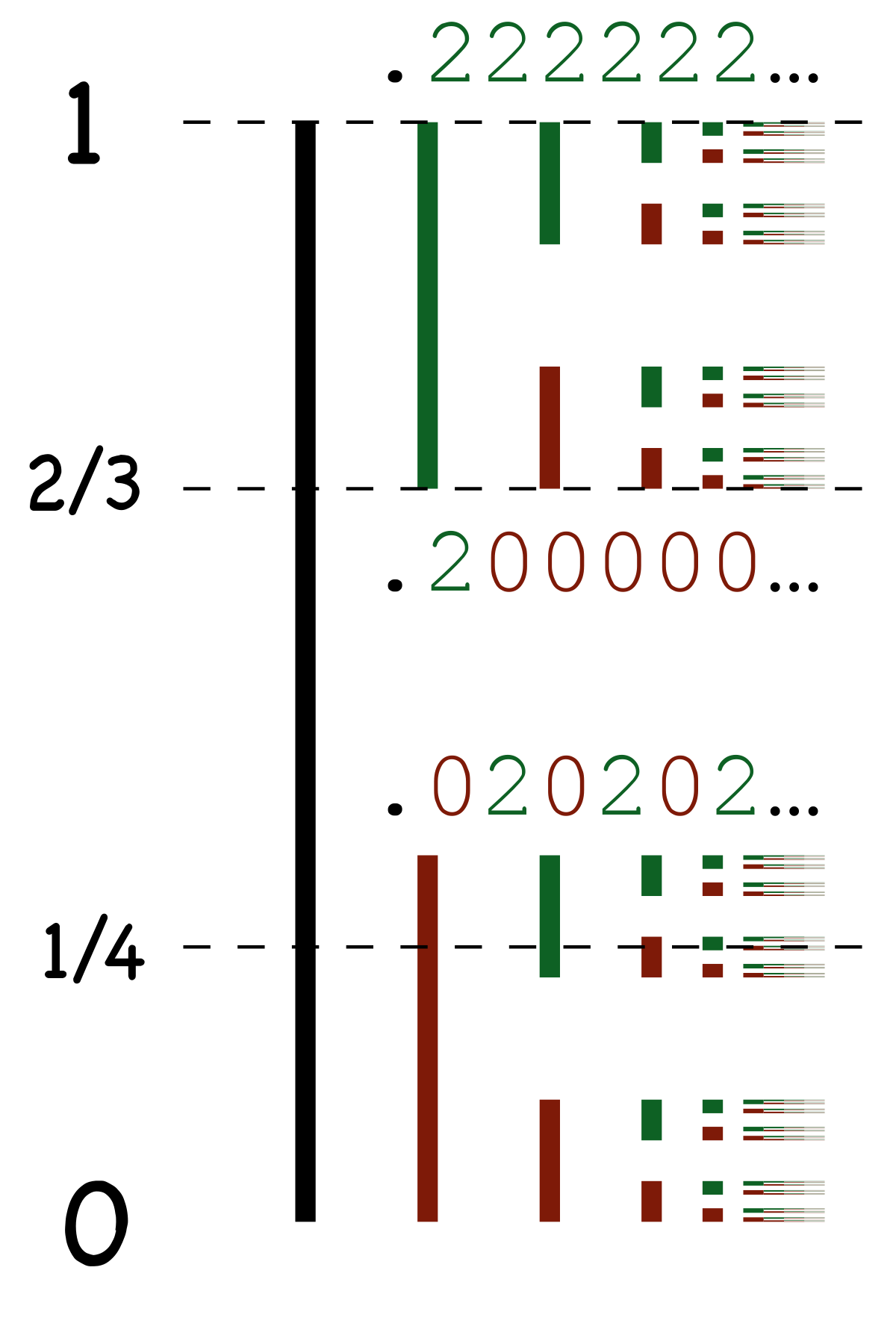
- un point dans l'intervalle unité
![\scriptstyle [0,1]](https://static.techno-science.net/illustration/Definitions/autres/0/088246d70e0c47595fc9931fcdb11d4c_ab56efa814d0eb44611b031b4ae3424a.png)



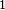
La


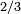
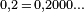
![\scriptstyle [0,1]](https://static.techno-science.net/illustration/Definitions/autres/0/088246d70e0c47595fc9931fcdb11d4c_ab56efa814d0eb44611b031b4ae3424a.png)
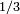
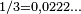
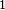
Les suites de

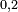
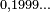

Généralisations
Le résultat que
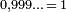
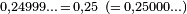
Deuxièmement, un théorème comparable s'applique dans toutes les bases. Par exemple, en base 2, (le système binaire),
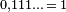
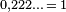
D'autres représentations de 1 existent aussi dans des bases non-entières. Par exemple, dans la base d'or, celle qui admet le nombre d'or comme base, les deux représentations standard de l'unité sont
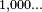
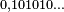
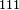



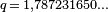
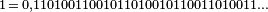
Une généralisation bien plus profonde concerne les systèmes de numération positionnels les plus généraux. Ils admettent aussi des représentations multiples, et dans un certain sens, avec de pires difficultés. Par exemple :
- Dans le système ternaire équilibré (en)
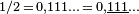
- Dans le système factoriel inversé (utilisant les bases 2, 3, 4, ... pour les positions après la virgule), on a :
Impossibilité d'une représentation unique
Le fait que tous ces divers systèmes de numérations souffrent de représentations multiples pour certains nombres réels peut être attribué à une différence fondamentale entre l'ensemble ordonné des nombres réels et les collections de suites infinies ordonnées en ordre lexicographique. En fait les deux propriétés suivantes rendent compte des difficultés :
- Si un intervalle des nombres réels est partitionné en deux parties non-vides L et R telles que tout élément de L est (strictement) inférieur à tout élément de R, alors : soit L contient un élément maximum ; soit R contient un élément minimum ; mais pas les deux à la fois.
- La collection de toutes les suites de symboles choisis dans n'importe quel « alphabet », ordonnées lexicographiquement peut être partitionnée en deux parties non-vides L et R, telles que tout élément de L est plus petit que tout élément de R, et ce, de manière que L possède un élément maximum et R un élément minimum. En effet, il suffit de prendre deux débuts de suite avec un nombre donné de symboles, identiques à part leurs derniers symboles, qui se suivent, soient p1 et p2. Puis il suffit de prendre pour L toutes les suites commençant au plus par p1 et pour R toutes les suites commençant au moins par p2. Alors L a un élément maximum : la suite commençant par p1 et continuant avec toujours le symbole le plus grand possible, et R a un élément minimum : la suite commençant par p2 et continuant avec le symbole le plus petit possible à toutes les positions.
La première propriété découle d'une propriété de base des réels : L a un supremum et R un infimum, et ils sont égaux, sinon, il y aurait un intervalle entre les deux, et L,R ne serait pas une partition. Une extension de l'argument montre que ce nombre appartient soit à L, soit à R, sinon, il y aurait 3 parties : L, R et l'extremum commun. Mais ce réel ne peut pas appartenir à la fois à L et à R, qui sont par hypothèse disjoints.
On aura reconnu comment le deuxième point généralise la situation obtenue avec 0,999... et 1,000... Nous n'avons fait nulle part l'hypothèse que le nombre de symboles admissibles soit le même à tous les éléments, ni même qu'ils soient indépendants les uns des autres. Dans ces conditions, la contradiction entre les propriétés énoncées montre qu'il ne peut pas y avoir de correspondance monotone et bijective entre une collection de suites de symboles et un intervalle des nombres réels : soit certains nombres ne correspondent à aucune suite, soit certains correspondent à plus d'une.
Marko Petkovšek a démontré que dans tout système positionnel susceptible de nommer tous les réels, l'ensemble des réels avec des représentations multiples est toujours dense. Il appelle la démonstration « un exercice instructif en topologie des ensembles de points » ; elle implique de considérer des ensembles de valeurs positionnelles, comme des espaces de Stone (en), et de remarquer que leurs représentations réelles sont données par des fonctions continues.