Développement décimal de l'unité - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Démonstrations algébriques - Démonstrations à partir de la construction des nombres réels - Démonstrations analytiques - Applications - Généralisations - Dans la culture populaire - Scepticisme dans l'enseignement - Problèmes connexes - Dans les systèmes de numération alternatifs - Bibliographie

Bibliographie

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « 0.999... »

Cet argument se trouve dans (, p. 186)
(, p. 39-41)
↑ ^{, , , et} ()
(, p. 61) Théorème 3.26 ; (, p. 706)
(, p. 170)
(, p. 69); (, p. 177)
Par exemple, (, p. 706), (, p. 61), (, p. 213), (, p. 180), (, p. 31)
(, p. 175), (, p. 115)
(, p. 22), (, p. 34)
(, p. 60-62) ; (, p. 29) ; (, p. 46)
(, p. 9, 11-12) ; (, p. 22) ; (, p. 27)
(, p. 12)
↑ ^et ()
(, §24.2 Suites)
(, p. 388, 393)
(, p. 395)
(, p. viii,395)
(, p. 408)
(, p. 503), (, p. 61)
(, p. 636)
(, p. 611), (, p. 409)
(, p. 410-411)
(, p. 301)
(, p. 1-3), (, p. 669,673), (, p. 96–98)
(, p. 97), (, p. 150-152), (, p. 507) et (, p. 29) donnent en exercice à effectuer cette description.
(, p. 50), (, p. 98)
(, p. 6-7)
↑ ^{, et} (, p. 221)
(, p. 6)
(, p. 10-14)
(, p. 5), (, p. 416–417)
(, p. 137–141)
(, p. 261–262)
Comme l'a observé (), citant ()
()
()
()
(, p. 439–442)
(, p. 245–247)
()
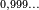
(, p. 175); la dicussion de $\scriptscriptstyle 0,999\ldots$ est étendue sur les pp.172-175
(), ()
(, p. 98), (, p. 60)
↑ ^et (, p. 11)
(, p. 14–15)
(, p. 901)
(, p. 902–903)
(, p. 51), (, p. 17)
(, p. 54)
(, Exercice 1 (c))
(, p. 462), ()

Notes

La limite découle par exemple de (, p. 57), théorème 3.20e. Pour une approche plus directe, voir (, sect. 8.1) ex. 2(a), 6(b)
La synthèse historique est revendiquée par (, p. xiv), puis par (, p. 10) ; en fait les deux préfèrent les coupures de Dedekind aux axiomes. Pour l'utilisation des coupures dans les manuels, voir (, p. 10) ou (, p. 17). Pour les points de vue sur la logique, voir (, p. 10), (, p. ix) ou (, p. 30)
, p. 113 qualifie cette description : « L'idée derrière les coupures de Dedekind est qu'un nombre réel $\scriptstyle x$ peut être caractérisé en donnant un ensemble infini de rationnels, soit tous ceux qui lui sont inférieurs. Pour éviter une définition circulaire, il faut pouvoir caractériser les ensembles de réels que l'on peut obtenir de cette manière... »
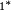
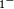
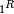
(, p. 17-20), () ou (, p. 119). Pour être plus précis, Rudin, Richman et Enderton appellent cette coupure $\scriptscriptstyle 1^\ast$ , $\scriptscriptstyle 1^-$ et $\scriptscriptstyle 1^R$ respectivement ; tous trois l'identifient avec le nombre 1 réel traditionnel. Noter que tandis que Rudin et Enderton l'appellent coupure de Dedekind, Richman l'appelle « coupure inessentielle de Dedekind »
(, p. 60) et (, p. 151) examinent la première méthode ; Mankiewicz l'attribue à Cantor, mais la source primitive n'est pas claire. (, p. 50) mentionne l'autre méthode.
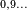
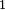
(, p. 119), (, p. 6). La dernière suggestion est due à (, p. 28) : « Le plus rassurant de tous les nombres est peut-être $\scriptscriptstyle 1$ ... Il est donc particulièrement dérangeant de voir quelqu'un faire passer $\scriptscriptstyle 0,9\ldots$ pour $\scriptstyle 1$ . »
Pour un traitement complet des nombres non-standard, voir par exemple ()
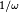
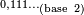
(, p. 79–80, 307–311) discutent $\scriptscriptstyle 1$ et $\scriptscriptstyle$ 1/3, et abordent $\scriptscriptstyle 1/\omega$ . Le jeu pour $\scriptscriptstyle 0,111\ldots_\mathrm{(base\ 2)}$ découle directement de la règle de Berlekamp, et est discuté par ()
(). (, p. 23) donne cette construction alternative (étendue à tous les rationnels) comme dernier exercice de son Chapitre I.
Voir par exemple le traitement par J. B. Conway les transformations de Möbius (, p. 47–57)

Liens internes

Sur les autres projets Wikimédia :

0.999... sur Wikimedia Commons (ressources multimédia)

Voir notamment :

* Développement décimal	* Décimale récurrente	* 1 (nombre)
* Série géométrique	* Série	* Infini
* Limite	* Nombre réel	* Analyse réelle
* Analyse non standard	* Mathématiques

Références externes

(en)Cecil Adams, « An infinite question: Why doesn't .999~ = 1? », 11 juillet 2003, The Straight Dope. Consulté le 24 avril 2010
(en) Alligood, Sauer et Yorke, Chaos: An introduction to dynamical systems, Springer, 1996 , chap. 4.1 (« Cantor Sets »).
Ce manuel d'introduction aux systèmes dynamiques est destiné aux étudiants du premier cycle et du début de deuxième cycle universitaire (p. ix)
(en) Tom M. Apostol, Mathematical analysis, Addison-Wesley, 1974, 2^e éd. .
Passage de l'analyse élémentaire à l'analyse avancée, Mathematical analysis a l'ambition d'être « honnête, rigoureux, à jour, et en même temps, pas trop pédant. » (préface). Les développements d'Apostol sur les nombres réels utilisent l'axiome de l'infimum et introduisent les développements décimaux deux pages plus loin (p. 9-11)
(en) R.G. Bartle et D.R. Sherbert, Introduction to real analysis, Wiley, 1982 .
Ce manuel vise à être « un manuel accessible, de rythme raisonnable, qui traite des concepts et techniques fondamentaux de l'analyse réelle ». Son développement sur les réels repose sur l'axiome du supremum (p. vii-viii)
(en) Richard Beals, Analysis, Cambridge University Press, 2004
(en) Elwyn R. Berlekamp, J.H. Conway et R.K. Guy, Winning Ways for your Mathematical Plays, Academic Press, 1982
(en) Martin Berz, Computer Arithmetic and Enclosure Methods: Automatic differentiation as nonarchimedean analysis, Elsevier, 1992, p. 439–450
Blizzard, « Blizzard Entertainment Announces .999~ (Repeating) = 1 », 1^er avril 2004, Blizzard Entertainment. Consulté le 24 avril 2010
(en) Bonnycastle, An Introduction to Algebra, 1811
(en) Bryan H. Bunch, Mathematical fallacies and paradoxes, Van Nostrand Reinhold, 1982 .
Ce livre présente une analyse des paradoxes et faussetés, comme un outil pour explorer son sujet central « la relation assez ténue entre réalité mathématique et réalité physique ». Il suppose connue l'algèbre de seconde ; les mathématiques supplémentaires sont apportées par le livre, y compris les séries géométriques au chapitre 2. Bien que $\scriptscriptstyle 0,999\ldots$ ne soit pas l'un des paradoxes entièrement traités, il est brièvement mentionné au cours d'un développement sur la méthode de Cantor. (p. ix-xi, 119)
(en) Brian Burrell, Merriam-Webster's Guide to Everyday Math: A Home and Business Reference, Merriam-Webster, 1998
(en) William Byers, How Mathematicians Think : Using Ambiguity, Contradiction, and Paradox to Create Mathematics, Princeton Universiy Press, 2007
(en) John B. Conway, Functions of one complex variable I, Springer, 1978, 2^e éd. .
Ce texte suppose « un solide cours de calcul analytique » comme préalable ; ses buts avoués sont de présenter l'analyse complexe comme « une introduction aux mathématiques » et d'en expliciter les matières avec clarté et précision. (p. vii)
(en) Charles Davies, The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications, A.S. Barnes, 1846
(en) Frank C. DeSua, « A system isomorphic to the reals », dans The American Mathematical Monthly, vol. 67, n^o 9, novembre 1960, p. 900–903
(en) Ed Dubinsky, Kirk Weller, Michael McDonald et Anne Brown, « Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2 », dans Educational Studies in Mathematics, vol. 60, 2005, p. 253–266
(en) Barbara Edwards et Michael Ward, « Surprises from mathematics education research: Student (mis)use of mathematical definitions », dans The American Mathematical Monthly, vol. 111, n^o 5, mai 2004, p. 411–425
(en) Robert Ely, « Nonstandard student conceptions about infinitesimals », dans Journal for Research in Mathematics Education, vol. 41, n^o 2, 2010, p. 117–146
Cet article est une étude de terrain concernant une étudiante, qui a mis au point une théorie des infinitésimaux à la Leibniz, pour s'aider à comprendre le calcul différentiel, et en particulier pour rendre compte que $\scriptscriptstyle 0,999...$ diffère de $\scriptscriptstyle 1$ par une valeur infinitésimale $\scriptscriptstyle 0,000...1\,.$
(en) Herbert B. Enderton, Elements of set theory, Elsevier, 1977 .
Un manuel de premier cycle universitaire en théorie des ensembles, qui ne « préjuge d'aucune formation ». Il est écrit pour accompagner un cours centré sur la théorie axiomatique des ensembles, ou sur la construction des systèmes numériques ; le matériel axiomatique est marqué afin de pouvoir être démystifié. (p. xi-xii)
(en) Leonhard Euler (trad. John Hewlett, Francis Horner), Elements of Algebra: Traduction anglaise, Orme Longman, 1822, 3^e éd.
(en) Finney, Weir et Giordano, Thomas' Calculus: Early Transcendentals, Addison–Wesley, New York, 2001, 10^e éd.
(en) Paul Fjelstad, « The repeating integer paradox », dans The College Mathematics Journal, vol. 26, n^o 1, janvier 1995, p. 11–15
(en) Anthony Gardiner, Understanding Infinity: The Mathematics of Infinite Processes, Dover, 2003
(en) Timothy Gowers, Mathematics: A Very Short Introduction, Oxford University Press, 2002
(en) Ivor Grattan-Guinness, The development of the foundations of mathematical analysis from Euler to Riemann, MIT Press, 1970
(en) H.B. Griffiths et P.J. Hilton, A Comprehensive Textbook of Classical Mathematics : A Contemporary Interpretation, Van Nostrand Reinhold, Londres, 1970 .
Ce livre est l'aboutissement d'un cours pour les professeurs de mathématiques du secondaire dans la région de Birmingham. Le cours était destiné à donner une perspective universitaire sur l'enseignement des mathématiques à l'école, et le livre vise les étudiants « qui ont en gros le niveau demandé après une année d'études spécialisées en mathématiques à l'université ». Les nombres réels sont construits au chapitre 24, « chapitre peut-être le plus difficile de tout le livre », bien que les auteurs attribuent une bonne partie de la difficulté à leur utilisation de la théorie des idéaux, qui n'est pas reproduite ici. (p. vii, xiv)
(en) K. Katz et M. Katz, « When is .999… less than 1 ? », dans The Montana Mathematics Enthusiast, vol. 7, n^o 1, 2010, p. 3–30
(en)Karin Usadi Katz, Mikhail G. Katz, « Zooming in on infinitesimal 1 − .9.. in a post-triumvirate era », 7 mars 2010, Educational Studies in Mathematics, Springer Verlag. Consulté le 24 avril 2010
(en) A.J. Kempner, « Anormal Systems of Numeration », dans The American Mathematical Monthly, vol. 43, n^o 10, décembre 1936, p. 610–617
(en) Vilmos Komornik et Paola Loreti, « Unique Developments in Non-Integer Bases », dans The American Mathematical Monthly, vol. 105, n^o 7, 1998, p. 636–639
(en) Herbert Kroemer et Charles Kittel, Thermal Physics, W. H. Freeman, 1980, 2^e éd. , p. 462
(en) W.G. Leavitt, « A Theorem on Repeating Decimals », dans The American Mathematical Monthly, vol. 74, n^o 6, 1967, p. 669–673
(en) W.G. Leavitt, « Repeating Decimals », dans The College Mathematics Journal, vol. 15, n^o 4, septembre 1984, p. 299–308
(en)Joseph Lewittes, « Midy's Theorem for Periodic Decimals », 2006, New York Number Theory Workshop on Combinatorial and Additive Number Theory, arXiv. Consulté le 23 avril 2010
(en) A.H. Lightstone, « Infinitesimals », dans The American Mathematical Monthly, vol. 79, n^o 3, mars 1972, p. 242–251
(en) Richard Mankiewicz, The story of mathematics, Cassell, Londres, 2000 .
Mankiewicz cherche à présenter « l'histoire des mathématiques de façon accessible » en combinant les aspects visuels et qualitatifs des mathématiques, les écrits de mathématiciens, et des ébauches historiques (p.8).
(en) Eli Maor, To infinity and beyond: a cultural history of the infinite, Birkhäuser, 1987 .
Revue de l'infini, par thèmes plutôt que chronologique, ce livre est « destiné au lecteur généraliste », mais « raconté du point de vue d'un mathématicien ». À propos du dilemme entre rigueur et lisibilité, Maor commente : « J'espère avoir convenablement résolu ce problème » (p. x-xiii).
(en) Joseph Mazur, Euclid in the Rainforest: Discovering Universal Truths in Logic and Math, Pearson: Pi Press, 2005
(en)MSDN, « Floating point types », 2010. Consulté le 24 avril 2010
(en) James R. Munkres, Topology, Prentice Hall, 2000, 2^e éd. .
Pensé comme une introduction à la topologie, « au niveau du 2^e cycle universitaire », sans connaissances préalables : « je ne suppose même pas que le lecteur en connaisse beaucoup en théorie des ensembles » (p. xi). Le traitement des réels par Munkres est axiomatique ; il prétend construire à la main : « Cette manière d'approcher le sujet demande pas mal de temps et d'efforts, et cela a une valeur plus logique que mathématique. » (p.30)
(en) Rafael Núñez, Do Real Numbers Really Move? Language, Thought, and Gesture: The Embodied Cognitive Foundations of Mathematics, vol. 18 : Unconventional Essays on the Nature of Mathematics, Springer, 2006 , p. 160–181
(en)J. J. O'Connor, E. F. Robertson, « History topic: The real numbers: Stevin to Hilbert », octobre 2005, MacTutor History of Mathematics. Consulté le 19 avril 2010
(en) George Pedrick, A First Course in Analysis, Springer, 1994
(en) Anthony Peressini, Dominic Peressini, Bart van Kerkhove (dir.) et Jean Paul van Bendegem (dir.), Perspectives on Mathematical Practices, vol. 5, Springer, 2007 , « Philosophy of Mathematics and Mathematics Education »
(en) Marko Petkovšek, « Ambiguous Numbers are Dense », dans American Mathematical Monthly, vol. 97, n^o 5, mai 1990, p. 408–411
(en) Márcia Pinto et David Tall, Following students' development in a traditional university analysis course, PME25, 2001, p. v4: 57–64
(en) M.H. Protter et Charles B. Morrey, A first course in real analysis, Springer, 1991, 2^e éd. .
Ce livre vise à « présenter une fondation théorique de l'analyse convenable pour les étudiants qui ont terminé un cours standard sur le calcul analytique » (p. vii). À la fin du chapitre 2, les auteurs supposent comme axiome pour les réels que des suites bornées non-décroissantes convergent, démontrant plus tard le théorème des segments imbriqués et la propriété du supremum (p. 56–64). Les développements décimaux apparaissent dans l'appendice 3, « développements des réels dans une base quelconque » (p. 503–507)
(en) Charles Chapman Pugh, Real mathematical analysis, Springer, 2001 .
Supposant le lecteur familier avec les rationnels, Pugh introduit les dès que possible, disant du traitement axiomatique : « Ceci est une sorte d'entourloupe, puisque toute l'analyse est fondée sur le système des réels. » (p. 10) Après avoir démontré la propriété du supremum et quelques faits connexes, les coupures ne sont plus utilisées pour le reste du livre.
(en) Fred Richman, « Is 0.999… = 1? », dans Mathematics Magazine, vol. 72, n^o 5, décembre 1999, p. 396–400
Le texte publié peut montrer quelques différences avec le preprint donné en lien, qui ne porte notamment pas la pagination.
(en) Abraham Robinson, Non-standard analysis, Princeton University Press, 1996
(en) Maxwell Rosenlicht, Introduction to Analysis, Dover, 1985 .
Ce livre donne une introduction « prudente et rigoureuse » à l'analyse réelle. Il donne les axiomes des réels, puis les construit (p. 27-31) comme des développements décimaux infinis, avec 0.999…=1 comme partie de la définition.
(en) Walter Rudin, Principles of mathematical analysis, McGraw-Hill, 1976, 3^e éd. .
Manuel pour un cours de second cycle universitaire avancé. « L'expérience m'a convaincu qu'il est pédagogiquement malavisé (bien que correct logiquement) de démarrer la construction des réels à partir des rationnels. Au début, la plupart des étudiants ne voient tout simplement pas pourquoi le faire. Donc on introduit le système des réels comme un corps ordonné satisfaisant la condition du supremum, et on en montre rapidement quelques propriétés. Cependant la construction de Dedekind n'est pas omise. Elle est mise en appendice du chapitre 1, où elle peut être étudiée et admirée quand le temps en est venu. »(p. ix)
(en) Maurice Shrader-Frechette, « Complementary Rational Numbers », dans Mathematics Magazine, vol. 51, n^o 2, mars 1978, p. 90–98
(en) Charles Smith et Charles Harrington, Arithmetic for Schools, Macmillan, 1895
(en) Houshang Sohrab, Basic Real Analysis, Birkhäuser, 2003
(en) Ian Stewart, The Foundations of Mathematics, Oxford University Press, 1977
(en) Ian Stewart, Professor Stewart's Hoard of Mathematical Treasures, Profile Books, 2009
(en) Ian Stewart, Calculus: Early transcendentals, Brooks/Cole, 1999, 4^e éd. .
Ce livre vise à « aider les étudiants à découvrir le calcul analytique » et à « se concentrer sur la compréhension des concepts » (p. v). Il omet les démonstrations des fondations du calcul analytique.
(en) D. O. Tall et R.L.E. Schwarzenberger, « Conflicts in the Learning of Real Numbers and Limits », dans Mathematics Teaching, vol. 82, 1978, p. 44–49
(en) David Tall, « Conflicts and Catastrophes in the Learning of Mathematics », dans Mathematical Education for Teaching, vol. 2, n^o 4, 1976
(en) David Tall, « Cognitive Development In Advanced Mathematics Using Technology », dans Mathematics Education Research Journal, vol. 12, n^o 3, 2000, p. 210–230
(de) Dr. Hans von Mangoldt, Einführung in die höhere Mathematik, Verlag von S. Hirzel, Leipzig, 1911, 1^re éd., « Chap. : Reihenzahlen »
(en)Hans de Vreught, « sci.math FAQ: Why is 0.9999… = 1? ». Consulté le 24 avril 2010
(en)A. N. Walker, « Hackenstrings and the 0.999… ?= 1 FAQ », 1999. Consulté le 24 avril 2010
(en) David Foster Wallace, Everything and more: a compact history of infinity, Norton, 2003

Lectures complémentaires

(en) S. E. Burkov, « One-dimensional model of the quasicrystalline alloy », dans Journal of Statistical Physics, vol. 47, n^o 3/4, 1987, p. 409
(en) Bob Burn, « 81.15 A Case of Conflict », dans The Mathematical Gazette, vol. 81, n^o 490, mars 1997, p. 109–112
(en) J. B. Calvert, E. R. Tuttle, Michael S. Martin et Peter Warren, « The Age of Newton: An Intensive Interdisciplinary Course », dans The History Teacher, vol. 14, n^o 2, février 1981, p. 167–190
(en) Younggi Choi et Jonghoon Do, « Equality Involved in 0.999… and (-8)⅓ », dans For the Learning of Mathematics, vol. 25, n^o 3, novembre 2005, p. 13–15, 36
(en) Tony Gardiner, « Infinite processes in elementary mathematics : How much should we tell the children ? », dans The Mathematical Gazette, vol. 69, n^o 448, juin 1985, p. 77–87
(en) John Monaghan, « Real Mathematics : One Aspect of the Future of A-Level », dans The Mathematical Gazette, vol. 72, n^o 462, décembre 1988, p. 276–281
(en) Malgorzata Przenioslo, « Images of the limit of function formed in the course of mathematical studies at the university », dans Educational Studies in Mathematics, vol. 55, n^o 1-3, mars 2004, p. 103–132
(en) James T. Sandefur, « Using Self-Similarity to Find Length, Area, and Dimension », dans The American Mathematical Monthly, vol. 103, n^o 2, février 1996, p. 107–120
(en) Anna Sierpińska, « Humanities students and epistemological obstacles related to limits », dans Educational Studies in Mathematics, vol. 18, n^o 4, novembre 1987, p. 371–396
(en) Jennifer Earles Szydlik, « Mathematical Beliefs and Conceptual Understanding of the Limit of a Function », dans Journal for Research in Mathematics Education, vol. 31, n^o 3, mai 2000, p. 258–276
(en) David O. Tall, « Dynamic mathematics and the blending of knowledge structures in the calculus », dans ZDM Mathematics Education, vol. 41, n^o 4, 2009, p. 481–492
(en) David O. Tall, « Intuitions of infinity », dans Mathematics in School, mai 1981, p. 30–33

Liens externes divers

(en).999999… = 1? de cut-the-knot (en)
(en)Pourquoi 0.9999… = 1 ?
(en)Demande à un spécialiste : décimales qui se répètent
(en)Démonstration de l'égalité basée sur l'arithmétique
(en)Les 9 qui se répètent
(en).999... qui se répètent égale 1
(en)Recherches de David Tall sur la connaissance en mathématiques
(en)Pourquoi est il faux de penser les nombres réels comme nombres avec une infinité de décimales ?
Théorème 0.999… = 1 en langage (en)Metamath
(en)Hackenstrings, et 0.999… ?= 1 FAQ
(en)Causerie amicale sur 0.999… = 1 ?

Dans les systèmes de numération alternatifs

La face cachée de la Lune révèle une étrangeté 🌓

Piéger le CO2 sous terre indéfiniment, c'est possible ! 🌍

La plus lointaine cousine de la Voie Lactée jamais observée 🌀

Ce codex médiéval cache un secret dans son bois 🔍

Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋

Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️

Des singularités temporelles dans l'Univers ? 🕰️

Des fossiles de dinosaures mieux datés 🦖

Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭

Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆

Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜

Le rôle méconnu de la décharge dans l'usure des batteries 🔋

La fonte des glaces déplace les pôles: quelles conséquences ? 🌍

L'appareil photo de votre smartphone peut détecter l'antimatière 📱

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Page générée en 0.213 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise