Électromigration - Définition

Introduction

Basiquement, on peut définir l'électromigration comme le déplacement d’atomes dans un conducteur induit par un flux d’électron. Ce mécanisme n’apparait que dans les applications où l’on observe de très forte densité de courant comme en microélectronique.

Image obtenue par MEB d’une défaillance provoquée par électromigration dans une interconnexion en cuivre. La couche de passivation a été supprimé par RIE et HF

Historique

Le phénomène d’électromigration a été découvert en 1861 par le physicien français Gerardin. Pendant longtemps le phénomène resta un sujet d’étude pour les physiciens car les conditions requisent pour observer le phénomène ne pouvaient être produites qu’en laboratoire.Il ne devient un sujet d’intérêt que pendant les années 60 avec l’émergence des circuits intégrés commerciaux, c’est-à-dire quand le phénomène est devenu préoccupant pour la fiabilité des lignes d’interconnexions. En effet dans une ligne électrique « aérienne » (comprendre non intégré), la densité de courant admissible est limitée à 10⁴ A.cm⁻² à cause de l’effet Joule qui provoquerai la fusion du conducteur. Dans un circuit intégré, le courant est conduit par des lignes constitués de fines couches de métal en contact avec du silicium qui joue le rôle de radiateur. Ceci permet d’atteindre (et même dépasser) les densités de courant nécessaire pour que l’électromigration devienne significative qui sont de l’ordre de 10⁶ A.cm⁻². C’est l’américain J. R. Black, dans un papier de 1967, qui pose les bases modernes de la recherche sur le sujet. Il exprime notamment la relation entre la densité de courant, la température et la durée de vie de la ligne dans une équation qui porte aujourd’hui son nom (équation de Black (en)).

Mécanisme de défaillance

La diffusion des atomes de métal n’est pas un problème en soit. Pour qu’un défaut apparaisse il faut que la quantité de matière arrivant dans une région soit supérieure ou inférieure à la quantité de matière la quittant. Si plus de matière arrive qu’il n’en part, l’accumulation de matière peut aboutir à un court-circuit ou à la rupture de la couche de passivation provoquant ainsi une opportunité de corrosion. Si plus de matière part qu’il n’en arrive, on observe une augmentation de la résistance de la ligne voir une ouverture de la ligne. Dans les lignes, les défauts apparaissent donc dans les zones de discontinuité du flux de matière comme les contacts avec le silicium ou aux vias (connexions entre les différents niveaux de métallisation).

Description

Quand on applique une différence de potentiels à une interconnexion, les électrons circulent du plus faible potentiel (cathode) vers le plus haut potentiel (anode). Les atomes de métaux commencent alors à se déplacer sous l’influence du flux d’électrons qui entre en interaction avec le réseau cristallin. Ce phénomène est appelé échange de quantité de mouvement (momentum exchange en anglais). En supposant que la direction du flux d’électrons est positive, la force induite par le flux d’électron peut être exprimée par :

où q ^* = Z ^* e est la charge atomique effective, Z ^* est le numéro atomique effectif, e est la charge de l’électron, E = ρj est le champ électrique, ρ est la résistivité du métal et j la densité de courant.

Le déplacement des atomes est facilité par la présence d’imperfections dans le cristal. Les régions de discontinuités dans la structure cristalline (dislocation) ou les interfaces entre les cristaux (joint de grains) sont, par exemple, des zones privilégiées pour la diffusion des atomes de métal. Quand une interconnexion est terminée par une barrière de diffusion comme le tungstène (W) ou le tantale (Ta), le déplacement des atomes provoque une contrainte de traction au niveau de la cathode où les atomes désertent et une contrainte de compression au niveau de l’anode où les atomes s’accumulent. Le gradient de stress résultant induit une force mécanique qui s’oppose à la force ``électronique. Cette force peut s’exprimer par :

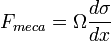
où Ω est le volume atomique, σ est le stress mécanique et x est la longueur de la ligne.

D’après le modèle de Korhonen, le flux atomique J_a peut être exprimé en fonction de F_elec et F_meca :

où C_a est la concentration atomique, D est la diffusivité atomique, k est la constante de Boltzmann et T est la température. Cette équation montre que | F_elec | doit être supérieur à | F_meca | pour que le flux des électrons provoque un déplacement de matière. L’influence de la température est par contre masquée puisque la température favorise l’électromigration contrairement à ce que l’équation pourrait faire penser. En effet, la diffusion est un processus activé thermiquement qui varie exponentiellement avec la température ( ).