Entier naturel - Définition

Ensemble des entiers naturels

Notations

La notation historique de l'ensemble des entiers naturels en imprimerie est « N », lettre capitale grasse. En écriture manuscrite (et particulièrement au tableau noir), ce caractère a été distingué du symbole de variable « N » par le doublement de la première barre verticale. Cette notation est rentrée dans l'usage dactylographique malgré les oppositions de mathématiciens de renom. La police blackboard gras propose un doublement de la barre oblique.

N

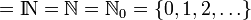
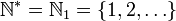
Pour lever l'ambiguïté au sujet de la prise en compte de zéro comme entier naturel, l'ensemble est parfois noté « N₀ ». L'indice 1 dénote alors au contraire l'exclusion de zéro. Mais l'usage consacre plus souvent pour cette restriction l'ajout d'un astérisque en exposant.

Dans le cadre de la théorie des ordinaux, l'ensemble des entiers naturels est un ordinal limite noté par la lettre minuscule grecque ω (oméga), voire ω₀ avec l'indice 0 comme pour le premier cardinal infini ℵ₀.

Propriétés

Les opérations d'addition et de multiplication étant associatives, commutatives, munies de neutres et satisfaisant une propriété de distributivité, l'ensemble des entiers naturels est un semi-anneau.

Il est ordonné pour la relation d'ordre usuelle induite par l'addition, qui lui donne une structure de bon ordre, c'est-à-dire que toute partie non vide admet un plus petit élément. Cette propriété est à la base du raisonnement par récurrence.

L'ensemble est également muni de la relation de divisibilité qui est un ordre partiel.

Son cardinal est le plus petit nombre cardinal infini, noté ℵ₀ (aleph zéro), définissant ainsi la notion de dénombrabilité.

Axiomatique de Peano

Quelle que soit la façon d'introduire les entiers naturels, ceux-ci ont les mêmes propriétés fondamentales à partir desquelles on développe l'arithmétique. Les axiomes de Peano sont un ensemble d'axiomes de second ordre proposés par Giuseppe Peano pour définir l'arithmétique. Ils sont au nombre de cinq :

1. l'élément appelé zéro et noté: 0, est un entier naturel.
2. Tout entier naturel n a un unique successeur, noté s(n) ou Sn.
3. Aucun entier naturel n'a 0 pour successeur.
4. Deux entiers naturels ayant même successeur sont égaux.
5. Si un ensemble d'entiers naturels contient 0 et contient le successeur de chacun de ses éléments, alors cet ensemble est égal à N.

Le premier axiome permet de poser que l'ensemble des entiers naturels n'est pas vide, le troisième qu'il possède un premier élément et le cinquième qu'il vérifie le principe de récurrence.