Forme bilinéaire - Définition

Produit tensoriel

Construction de formes bilinéaires

Si a^* (resp. b^*) est une forme linéaire de E (resp. de F), il existe une méthode simple de construire une forme bilinéaire sur ExF. Cette forme est notée a^*b^* et est définie par :

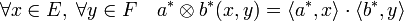
Cette opération s'appelle le produit tensoriel de a^* et b^*. L'espace E^*F^* désigne le sous-espace vectoriel de L₂(E,F) engendré par l'image du produit tensoriel. Un vecteur x de E peut être identifié à une forme linéaire sur E^*. En effet, à une forme linéaire a^*, elle associe le scalaire <a^*, x>. Cette remarque permet de considérer le produit tensoriel d'un élément de E et d'un élément de F qui est une forme bilinéaire sur E^*xF^*.

Le fait d'utiliser un espace ou son dual possède une signification profonde en physique. Pour cette raison, si l'ensemble de départ est un espace dual, les physiciens utilisent le terme de contravariant et dans le cas contraire de covariant. Le premier produit tensoriel présenté ici est deux fois contravariant.

Propriétés

L'image de E^*xF^* par le produit tensoriel n'est pas l'ensemble des formes bilinéaires de ExF, ce n'est pas non plus un espace vectoriel. En revanche il possède d'autres propriétés :

• L'application produit tensoriel de E^*xF^* dans L₂(E, F) est bilinéaire, commutative.

• L'égalité suivante (EF)^* = E^*F^* est vérifiée.

• L'image de E^*xF^* par le produit tensoriel est un cône. Il est générateur de L₂(E, F) si E et F sont de dimension finie.

Deux produits supplémentaires sont développés le produit extérieur et le produit symétrique. Appliqué à deux vecteurs a^* et b^* de E^* on obtient :

Produit symétrique :

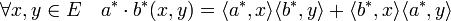
Produit extérieur :

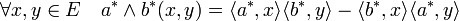
On obtient l'égalité :

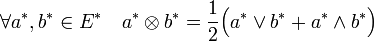
• Le produit extérieur (resp. symétrique) a son image incluse dans les formes bilinéaires alternées (resp. symétrique).
• Les espaces vectoriels engendrés par les produits extérieurs et symétriques sont en sommes directes. En dimension finie, le premier espace est de dimension n(n - 1)/2 et le deuxième n(n + 1)/2.

• L'application produit tensoriel de E^*xF^* dans L₂(E, F) est bilinéaire :

C'est une conséquence immédiate de sa définition. Soit a^* et b^* deux vecteurs de E^*, c^* un vecteur de F^* et λ un scalaire.

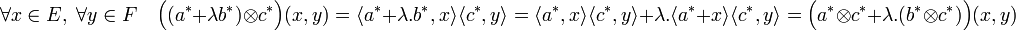
La commutativité se démontre de même.

• L'égalité suivante (EF)^* = E^*F^* est vérifiée :

En effet, (EF)^* désigne le dual des formes bilinéaires sur E^*xF^*. Soit x (resp. y) un élément de E (resp. F) et α un élément de (EF)^*. Soit φ l'application qui à α associe φ_α la forme bilinéaire sur ExF, c'est-à-dire l'élément de E^*F^* suivant :

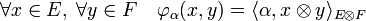
L'application φ_α est manifestement biliénaire de ExF et φ est est linéaire.

Montrons qu'elle est injective : Si α est élément du noyau de φ, alors φ_α est nul sur une famille génératrice de EF et donc α est la forme nulle.

Montrons qu'elle est surjective : Il suffit pour cela de montrer que si a^* (resp. b^*) est un élément du dual de E (resp. de F), alors a^*b^* possède un antécédent par φ.

• L'image de E^*xF^* par le produit tensoriel est un cône :

Si a^*, (resp. b^*) est un élément de E^* (resp. de F^*) et Il suffit de remarquer que : Soit β l'élément de (EF)^* défini par :

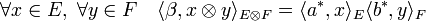
Alors, par construction φ_β = a^*b^*, ce qui termine la démonstration.

• L'image de E^*xF^* par le produit tensoriel est un cône :

Si b est une forme bilinéaire de E^*xF^*, alors il existe un vecteurs x^* (resp. y^*) de E^* (resp. F^*) tel que b est égal à x^*y^*. Si λ est un scalaire, alors λb est égal à (λx^*)y^* est fait partie de l'image du produit tensoriel.

• L'image de E^*xF^* par le produit tensoriel est générateur de L₂(E, F) si E et F sont de dimension finie :

Soit n (resp. m) la dimension de E (resp. de F). Le théorème sur la dimension d'un espace d'applications linéaires montre que L(E, F^*) est de dimension n.m. Si (e_i^*) (resp. (f_j^*)) est une base de E^* (resp. de F^*), la famille e_i^*f_j^* est libre et de même dimension que L(E, F^*) qui est isomorphe à L₂(E, F). Cette propriété montre que cette dernière famille est une base et démontre la proposition.

• L'ensemble des formes bilinéaires symétriques (respectivement antisymétriques) forme un sous-espace vectoriel. Ces deux sous espaces vectoriels sont en somme directe :

Le fait que la somme ou la multiplication scalaire soit stables pour les deux ensembles est évident. Ce sont donc des sous-espaces vectoriels.

L'égalité suivante montre que toute forme bilinéaire est la somme d'une forme symétrique et d'une antisymétrique. Leur somme engendre l'espace des formes bilinéaires:

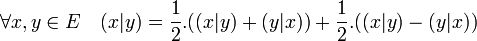
L'intersection des deux sous-espaces est de manière évidente réduite à la forme nulle.

 

Complexifié d'un espace vectoriel

Un exemple simple correspond au complexifié d'un espace vectoriel réel. Si E désigne un espace vectoriel réel, de dimension finie ou non, et si C l'ensemble des nombres complexes considéré ici comme un espace vectoriel réel de dimension deux. Le corps C est identifié avec son dual avec l'application qui à un complexe λ associe l'application μ → Reλ.Reμ+Imλ.Imμ. Alors CE est l'espace vectoriel des formes bilinéaires de CxE^* (la forme associée à E^* est un élément de E identifié au bidual). l'espace CxE^* est muni d'une multiplication naturelle sur C :

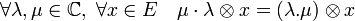
• Dans CE tout vecteur est somme d'un produit tensoriel de 1 et d'un vecteur de E et de i et d'un autre vecteur de E.

• Si (e_j) est une base de E, alors (1e_i) est une base de CE en tant que C espace vectoriel.

Il est fréquent que E soit identifié à 1E.

• Dans CE tout vecteur est somme d'un produit tensoriel de 1 et d'un vecteur de E et de i et d'un autre vecteur de E :

Soit b une forme bilinéaire de CxE^*. Elle vérifie la proposition suivante :

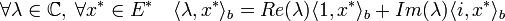
donc

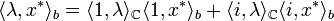
L'application qui à x^* associe <1,x^*> (resp. <i,x^*>) est une forme linéaire que l'on note x₁ (resp. x_i). On obtient :

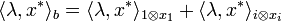
Ce qui termine la démonstration.

• Si (e_j) est une base de E, alors (1e_i) est une base de CE en tant que C espace vectoriel.

La démonstration est immédiate, la proposition précédente montre que tout élément de si y est un élément de CE, alors :

 

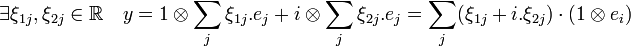
Dimension trois

Si E est un espace vectoriel de dimension trois, alors l'espace des formes bilinéaires alternées est aussi de dimension trois, car cet espace est de dimension n(n-1)/2. De même que le produit scalaire permet d'identifier un élément du dual avec un vecteur de l'espace, il est aussi possible d'identifier une forme bilinéaire alternée à un vecteur de E. L'application qui à trois vecteurs x, y, z associe le déterminant dans une base B : det (x, y, z)_B est une application trilinéaire alternée. Cette application ne dépend pas du choix de la base, à condition qu'elle soit orthonormale et orienté. Elle prend le nom de produit mixte, il est noté [x, y, z]. Il permet d'identifier un vecteur c de E à la forme m_c suivante :

Cette application m qui à un vecteur associe une forme bilinéaire alternée est un isomorphisme de E dans l'ensemble des formes bilinéaires alternée en dimension trois. À l'image de l'identification avec de E avec son dual grâce au produit scalaire. En dimension trois, les physiciens identifient E avec l'espace des formes bilinéaires alternées grâce à l'isomorphisme m. Ainsi, si a et b sont deux vecteurs de E et c le vecteur tel que ab est égal à m_c, les physiciens écrivent :

Si (.|.) désigne le produit scalaire de E, cette définition entraine :