Forme bilinéaire - Définition
La liste des auteurs de cet article est disponible ici.
Forme bilinéaire et application linéaire
Dual
Le dual E* est l'espace des formes linéaires de E dans K le corps sous-jacent de l'espace vectoriel E. Il existe une forme bilinéaire canonique sur E*xE. elle associe à tout couple formé d'un élément du dual f * et d'un élément x de l'espace, l'image du vecteur par la forme linéaire.
-
- La forme bilinéaire canonique sur E*xE est non dégénérée.
En effet par définition la seule forme linéaire nulle sur E est la forme nulle. Le noyau à gauche est donc réduit à la forme nulle. Si x est un vecteur non nul de E, il existe une forme linéaire qui vaut un en x et zéro sur un hyperplan supplémentaire de la droite engendrée par x. Le seul vecteur qui annule toutes les formes linéaires est donc le vecteur nul, ce qui montre que le noyau au droite est aussi réduit au vecteur nul.
Cette forme bilinéaire joue un rôle particulier, elle permet d'exprimer toutes les formes bilinéaires. Soit (.|.) une forme bilinéaire de ExF. Si x est un élément de E, alors ( x|. ) est un élément du dual de F. Soit φ1 l'application de E vers F*, qui à x associe la forme linéaire ( x|. ). On peut définir de même une application φ2 de F vers le dual de E. On dispose des égalités suivantes :
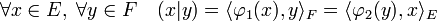
-
- Les applications φ1 et φ2 sont linéaires.
Cette propriété est la conséquence directe de la bilinéarité de la forme (.|.).
Noyau
La structure des applications φ1 et φ2 permettent de comprendre la géométrie des noyaux :
-
- Le noyau de φ1 (resp. φ2) est le noyau à gauche (resp. à droite) de la forme bilinéaire.
Le corollaire immédiat est que les noyaux à gauche et à droite sont des sous-espaces vectoriels.
Soient N1 (resp. N2) le noyau à gauche (resp. à droite) de la forme bilinéaire et M1 (resp. M2) des supplémentaires de N1 (resp. N2). Leur l'existence dans le cas général suppose l'utilisation de l'axiome du choix.
-
- La restriction de la forme bilinéaire à M1xM2 est non dégénérée. Le projecteur p1 (resp. p2) sur M1 (resp. M2) parallèlement à N1 (resp. N2) vérifie la propriété suivante :
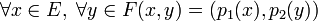
La forme bilinéaire se réduit à une forme non dégénérée une fois que les deux noyaux ont été retirés. Ce retrait permet toujours une détermination exacte de la forme bilinéaire. En dimension finie, la propriété suivante est vérifiée :
-
- La dimension de M1 est égale à celle de M2.
-
- La forme bilinéaire est non dégénérée si et seulement si φ1 est un isomorphisme. Alors φ2 est aussi un isomorphisme.
-
- La restriction de la forme bilinéaire à M1xM2 est non dégénérée et le projecteur p1 (resp. p2) sur M1 (resp. M2) parallèlement à N1 (resp. N2) vérifie la propriété suivante :
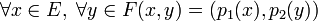
Pour tout élément m1 de M1 il existe un vecteur y de F non orthogonal à m1. En effet, cet élément n'est pas dans le noyau de la forme bilinéaire. Le vecteur y se décompose en somme d'un élément m2 de M2 et n2 de N2. On a alors :
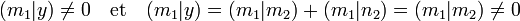
La dernière égalité montre que le noyau à gauche de la restriction est réduit au vecteur nul. Un raisonnement analogue montre que le noyau à droite est aussi réduit au vecteur nul.
La dernière propriété provient du fait que x - p1(x) (resp. y - p1(y)) est un élément du noyau à gauche (resp. à droite), en conséquence :
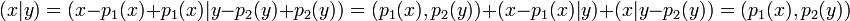
-
- La dimension de M1 est égale à celle de M2 :
Cette propriété est une conséquence de la proposition précédente. L'image par φ1 de M1 est incluse dans l'ensemble des formes bilinéaires de M2 sa dimension ne dépasse pas celle du dual de M2 et donc celle de M2 car en dimension finie un dual a même dimension que l'espace direct. L'application φ1 restreinte à M1 possède un noyau réduit au vecteur nul, en conséquence M1 a même dimension que son image par φ1. Ceci démontre que la dimension de M1 est inférieure ou égale à celle de M2. Le même raisonnement montre que la dimension de M2 est aussi inférieure ou égale à celle de M1, ce qui permet de conclure.
-
- La forme bilinéaire est non dégénérée si et seulement si φ1 est un isomorphisme, alors φ1 est aussi un isomorphisme :
Si la forme bilinéaire est non dégénérée alors les deux noyaux sont réduits au vecteur nul et les dimensions de E et de F sont égales d'après la proposition précédente. Alors φ1 est injectif car son noyau est réduit au vecteur nul et l'égalité des dimensions de E et du dual de F montre la surjectivité. Un raisonnement analogue montre que φ2 est aussi un isomorphisme.
Réciproquement si φ1 est un isomorphisme son noyau est réduit au vecteur nul, et l'image de φ1 est le dual entier de F. Un vecteur y de F orthogonal à tous les éléments de E est orthogonal au dual de F pour la forme <., .>F. Un seul vecteur vérifie cette propriété, le vecteur nul, en conséquence le noyau à droite est aussi réduit au vecteur nul, ce qui termine la démonstration.
Orthogonalité
La notion de noyau peut être étendue :
-
- L'ensemble des vecteurs dont l'image par la forme bilinéaire avec tous les éléments d'une famille de vecteurs Φ de E est nulle est un sous-espace vectoriel de F appelée orthogonal de Φ. Cet ensemble est souvent noté
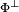
- L'ensemble des vecteurs dont l'image par la forme bilinéaire avec tous les éléments d'une famille de vecteurs Φ de E est nulle est un sous-espace vectoriel de F appelée orthogonal de Φ. Cet ensemble est souvent noté
L'orthogonal d'une famille de vecteurs de F est évidemment aussi un sous-espace vectoriel. Cet espace vectoriel contient le noyau à gauche de la forme bilinéaire. À l'aide de cette définition les noyaux apparaissent comme l'orthogonal des espaces E et F.
-
- L'orthogonal de
- L'orthogonal de
-
- Soit E1 et E2 deux sous-espaces vectoriels de E, alors l'orthogonal de la somme de E1 et E2 est l'intersection des orthogonaux. L'orthogonal de l'intersection est la somme des orthogonaux :
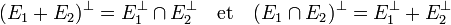
En dimension finie, on dispose de plus de l'égalité suivante :
-
- La dimension de
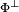
- La dimension de
Un corollaire de ce cas particulier indique que l'orthogonal de
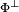
-
- L'orthogonal de Φ est un sous-espace vectoriel de F :
L'orthogonal de Φ contient au moins le vecteur nul, il suffit de montrer qu'il est stable par combinaison linéaire pour démontrer cette proposition. Soit y1, y2 deux vecteurs de l'orthogonal de Φ, λ un scalaire et x un vecteur de la famille Φ :
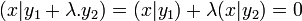
La dernière égalité montre la stabilité par combinaison linéaire et permet de conclure.
-
- L'orthogonal de
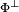
- L'orthogonal de
L'orthogonal de
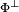
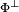
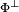
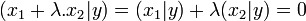
La dernière égalité et le fait que tout élément de Φ est orthogonal à tout élément de
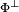
-
- Soit E1 et E2 deux sous-espaces vectoriels de E, alors l'orthogonal de la somme de E1 et E2 est l'intersection des orthogonaux et l'orthogonal de l'intersection est la somme des orthogonaux : :
Tout vecteur de l'orthogonal de la somme E1 + E2 est à la fois orthogonal aux éléments de E1 et de E2, l'orthogonal de cette somme est donc incluse dans l'intersection des orthogonaux. Réciproquement tout vecteur de l'intersection est bien orthogonal à chaque vecteur de E1 et de E2 et donc à leur somme car l'orthogonal d'une famille est un sous-espace vectoriel.
La deuxième partie de la proposition se démontre de manière analogue.
-
- La dimension de
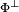
- La dimension de
Soit n la dimension de F et (f1*,..., fp*), où p est un entier strictement inférieur à n, une base de
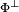
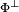
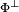
Applications linéaires de l'espace vers le dual
Le paragraphe précédent montre l'existence d'une application canonique des formes bilinéaires de ExF vers l'espace des applications de E dans le dual F*. Soit (.|.)b une forme bilinéaire et ψ1b l'application, qui à x élément de E associe la forme linéaire de F (x|.)b. L'application ψ1, qui à (.|.)b associe ψ1b est une fonction de L2(ExF) dans L(E,F*). On définit de même une application ψ2 de L2(ExF) dans L(F,E*).
-
- L'ensemble des formes bilinéaires de ExF forme un espace vectoriel.
-
- L'application ψ1 (resp. ψ2) est un isomorphisme de L2(ExF) dans L(E,F*) (resp. L(F,E*).
Montrons que ψ1 est injective. Soit k un élément du noyau, alors ψ1k a pour image par tout vecteur de E la forme linéaire nulle, par définition d'un élément du noyau, l'application est donc bien injective. Elle est aussi surjective, en effet, soit f une application de L(E,F*), alors la forme bilinéaire qui au couple (x,y) associe <f(x), y> est un antécédent.
A la différence du paragraphe précédent, ce résultat ne tombe jamais en défaut, même en dimension infinie. Une forme bilinéaire b se représente ainsi par deux applications linéaires ψ1b et ψ2b. Elles sont liés par les égalités suivantes :
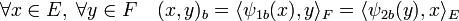
Les différents isomorphismes montrent que l'application qui à ψ1b associe ψ2b est un isomorphisme. On dit que ψ2b est l'application linéaire transposée de ψ1b. La définition est proche de celle plus topologique d'adjoint. L'application qui, à une application linéaire associe sa transposée, est un isomorphisme car composée d'isomorphismes.
En dimension finie, cette proposition possède le corollaire suivant :
-
- Si E et F sont de dimension finie alors la dimension de L2(ExF) est le produit des dimensions de E et de F.
Cette proposition découle directement du fait que la dimension de l'espace des applications linéaires d'un espace de dimension finie dans un espace de dimension finie.
Représentation matricielle
Soient E, F deux espaces vectoriels de dimension finie,
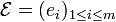
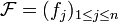
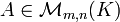
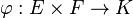
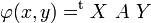
les coordonnées X (resp. Y) étant disposées sous forme d'une matrice colonne de m (resp. n) éléments de K, et tX désignant la matrice ligne transposée de X.
Inversement, l'application bilinéaire

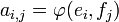
Ceci permet de définir (les bases
La formule de changement de base pour les formes bilinéaires est différente de celle pour les applications linéaires : on pourra comparer les deux dans l'article Matrice de passage.

















































