Idéal premier - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Entiers relatifs
Dans Z, un entier premier au sens de la définition précédente est un entier tel que Z/n Z soit intègre. Tout anneau intègre ayant un nombre fini d'éléments est un corps. En conséquence soit n est un nombre premier au sens usuel, soit -n est un nombre premier.
La définition de l'article correspond à la définition usuelle aux inversibles près. En effet, par convention, un nombre premier est l'élément associé positif des générateurs de l'idéal. Cette convention permet une expression plus simple du théorème fondamental de l'arithmétique (cf l'article élément inversible).
Polynôme
Polynôme à coefficient dans un corps
Dans le cas où les polynômes sont à coefficient dans un corps, l'anneau est, comme précédemment euclidien, donc principal : tout idéal est composé des multiples d'un polynôme unitaire. Un polynôme est premier si, et seulement s'il est différent d'une constante et si toute décomposition en deux facteurs contient un élément inversible.
Cette définition est équivalente à celle d'élément irréductible. Cet état de fait est général dans les anneaux principaux. La tradition impose surtout de parler de polynôme irréductible.
Polynôme à coefficient dans Z
Si les coefficients du polynôme sont choisis dans Z, alors l'anneau des polynômes n'est plus principal. Par exemple, l'idéal I engendré par X et 2 n'est pas principal. Le quotient de Z[X] par I est un anneau à deux éléments donc intègre. Cet idéal est premier, mais n'est pas associé à un élément de l'anneau.
Entier de Gauss
Les entiers de Gauss forment un anneau euclidien. À chaque idéal correspond une classe d'association engendrant l'idéal, les notions d'idéaux et de nombres premiers de Gauss coïncident. Les éléments premiers s'appellent des nombres premiers de Gauss.
Définition
Dans toute la suite de l'article, A désigne un anneau commutatif unitaire, a un élément de A et I un idéal de A.
-
- Un idéal I de A est dit premier si le quotient de A par I est intègre.
-
- Un élément a de A est dit premier si, et seulement si l'idéal a.A est premier.
Lorsque A est intègre, cette définition généralise la notion de nombre premier, tout en conservant les propriétés : si un élément non nul p est premier, alors toute décomposition de p en deux facteurs contient un élément inversible (mais il existe des contre-exemples où A n'est pas intègre. Prendre l'élément premier p=(1,0) de l'anneau Z² ).
Propriétés
Lemme d'Euclide
La traduction du lemme d'Euclide est directe en termes d'idéal :
-
- Un idéal I est premier si et seulement si c'est un idéal propre tel que :
-
![\forall a,b\in A\quad[a.b\in I\Rightarrow(a\in I\mbox{ ou }b\in I)]](https://static.techno-science.net/illustration/Definitions/autres/0/011d7ae6143e4801edd40a4c3cad5b40_637f4a455681f22f5b3b9bb090f74f0e.png)
![\forall a,b\in A\quad[a.b\in I\Rightarrow(a\in I\mbox{ ou }b\in I)]](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/011d7ae6143e4801edd40a4c3cad5b40_637f4a455681f22f5b3b9bb090f74f0e.png)
Cette proposition est en effet l'analogue de : un entier supérieur à 1 est premier si chaque fois qu'il divise un produit, il divise l'un des facteurs.
De manière équivalente :
-
- Un idéal propre est premier si et seulement si chaque fois qu'il contient le produit de deux idéaux, il contient l'un ou l'autre.
Cette propriété peut être affinée :
-
- Un idéal propre est non premier si et seulement s'il est strictement contenu dans deux idéaux dont il contient le produit.
Soit I un idéal propre (c'est-à-dire distinct de A), autrement dit A / I est différent de l'anneau réduit à l'élément nul.
-
- Première caractérisation :
I est premier si et seulement si A / I est intègre, c'est-à-dire si et seulement si
![\forall a,b\in A\quad[\overline a.\overline b=\overline 0\Rightarrow(\overline a=\overline 0\mbox{ ou }\overline b=\overline 0)]](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4c8748cdb1eefbe8bf35b4b7121f052f_60d026a8f105ec5ecdd745d3e4418487.png)
Mais dire que
-
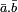
- Si I est premier et ne contient ni l'idéal J, ni l'idéal K, alors il ne contient pas leur produit :
En effet, il existe dans ce cas a (resp. b) élément de J (resp. de K) non éléments de I. Alors a.b est un élément de J.K qui ne peut être élément de I car I est premier.
-
- Si I n'est pas premier alors il existe deux idéaux J et K tels que I contienne le produit J.K mais soit strictement contenu dans J et K (donc ne contienne ni l'un ni l'autre) :
En effet, dans ce cas, il existe dans l'anneau deux éléments a et b n'appartenant pas à I mais dont le produit appartient à I. Les idéaux J=I+(a) et K=I+(b) contiennent alors strictement I, tandis que le produit J.K est inclus dans I.
Par conséquent, tout idéal premier est irréductible : s'il est égal à l'intersection de deux idéaux alors il est égal à l'un ou l'autre (puisqu'il contient leur produit et qu'il est premier).
Anneau principal
Dans un anneau principal, un idéal premier ressemble à l'idée intuitive que l'on s'en fait d'après l'exemple des entiers relatifs.
Si I est un idéal non nul d'un anneau principal, les propositions suivantes sont équivalentes :
- (i) I est premier
- (ii) I est engendré par un élément p non inversible et qui, s'il divise un produit a.b, divise soit a soit b.
- (iii) I est engendré par un élément p non inversible et qui n'a d'autres diviseurs que lui-même et 1 aux éléments inversibles près
- (iv) I est maximal.
Supposons I engendré par p.
- (i) ⇒ (ii)
Les éléments de I sont les éléments divisibles par p. Le lemme d'Euclide permet de conclure.
- (ii) ⇒ (iii)
Soient a et b deux éléments de A tels que p = a.b, alors (ii) nous apprend que p divise soit a soit b, en conséquence (puisque p est non nul et que A est intègre) p est associé soit à a soit à b et l'autre facteur est inversible.
- (iii) ⇒ (iv)
Tout idéal contenant I est engendré par un diviseur de p, donc est engendré soit par 1, soit par p. En conséquence, les deux seuls idéaux contenant I sont A et I, ce qui est la définition d'un idéal maximal.
- (iv) ⇒ (i)
Si I est maximal alors A/I est un corps donc est intègre, donc I est premier.
Image réciproque
Si ψ est un morphisme d'anneaux (commutatifs et unitaires) de A dans B, et P un idéal de B, on sait que l'image réciproque Q de P par ψ est un idéal de A. Dans ces conditions, si P est premier alors Q aussi.
En effet A / Q est intègre : d'une part A / Q n'est pas l'anneau nul, autrement dit Q n'est pas A tout entier, car il ne contient pas 1A puisque ψ(1A)=1B n'appartient pas à P ; d'autre part A / Q est isomorphe à un sous-anneau de B / P, donc est, comme lui, sans diviseur de zéros.
Cette propriété s'applique le plus souvent au cas où A est un sous-anneau de B, le morphisme ψ étant alors simplement l'injection canonique. Elle se formule alors ainsi :
Si A est un sous-anneau de B et P un idéal premier de B alors P∩A est un idéal premier de A.
