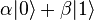Informatique quantique - Définition

Les bases physiques

L'informatique quantique est basée sur la mécanique quantique. Les phénomènes utiles sont l'intrication quantique et la superposition. Il est cependant nécessaire de prévoir les effets contre-productifs de la décohérence.

Fonction d'onde

La fonction d'onde en mécanique quantique est la représentation de l'état quantique dans la base de dimension infinie des positions. La probabilité de présence des particules représentées par cet état quantique est alors directement le carré de la norme de cette fonction d'onde.

État quantique

En mécanique quantique, on représente l'état d'un système par un point dans un espace vectoriel hilbertien ; l'espace à considérer dépendant du système étudié. On utilise souvent la notation bra-ket pour représenter les états quantiques de manière simple. Par exemple, l'espace des états d'une particule sans spin est l'espace des fonctions de à carré sommable. Lorsque l'on associe deux systèmes pour en faire un plus gros, l'espace des états de ce gros système est le produit tensoriel des espaces des états associés aux deux sous-systèmes.

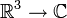
On retrouve également le déterminisme de la mécanique classique, c'est-à-dire que l'on peut calculer comment l'état d'un système va évoluer au cours du temps (grâce à l'équation de Schrödinger), sauf lorsqu'il y a une mesure de l'état de notre système, auquel cas l'évolution n'est plus déterministe, mais probabiliste.

Il s'agit là d'une différence majeure avec la mécanique classique, qui découle du postulat de réduction du paquet d'onde et qui permet de donner une interprétation probabiliste aux états quantiques.

Supposons qu'un système quantique se trouve dans un état et que l'on veuille mesurer une observable du système (énergie, position, spin, ...). Les vecteurs propres de sont notés et les valeurs propres correspondantes α_i, que l'on supposera non dégénérées pour simplifier. Comme le postule le principe de réduction du paquet d'onde, la mesure de A ne peut donner comme résultat que l'un des α_i, et la probabilité d'obtenir le résultat α_i est . Supposons que la mesure donne pour résultat α_p, le système est passé lors de la mesure et de façon instantanée de l'état à l'état .

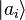
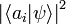
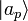
On voit dès lors l'interprétation que l'on peut faire des produits scalaires , où est un état quelconque : en effet, en supposant l'existence d'une observable dont serait un des états propres, on peut dire que la probabilité de trouver le système dans l'état (sous-entendu : si on faisait la mesure) est . Pour cette raison, le produit scalaire est appelé amplitude de probabilité.

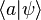
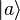
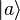
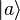
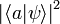
Il existe d'autres représentations mathématiques de l'état d'un système, la matrice densité étant une généralisation de la représentation exposée ici.

Intrication quantique

En mécanique quantique, on appelle intricat un état physique où est intriqué un système S1 & un système S2 sans que l'espace de Hilbert soit la somme tensorielle de l'espace de S1 et de l'espace S2. Il y a même au contraire corrélation complète de S1 et de S2 de sorte que l'entropie de (S1 union S2) dans un intricat est simplement celle de S2 ou de S1. Il y a sous-additivité complète.

L'intrication quantique est la ressource naturelle principale, utilisée en informatique quantique : actuellement, on la compare même au fer, tel que considéré à l'âge du bronze. De fait, la théorie de l'informatique quantique a beaucoup progressé depuis que l'on sait réaliser des intricats de faible décohérence : alors il est devenu pensable de prévoir un futur ordinateur quantique. Les mathématiciens (Shor, Kitaev, ...) ont fondé le tout nouveau calcul quantique, qui est en train de révolutionner le calcul de la complexité algorithmique.

Bits vs qubits

Les opérations ne sont plus appliquées à des bits, mais à des qubits. L'espace des états possibles n'est pas le même que dans le monde classique. Les deux qubits possibles sont et . Une différence majeure d'avec les bits, c'est qu'un qubit peut être dans les deux états en même temps : c'est le phénomène de superposition. En général, un qubit est

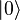
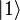
où | α | ² + | β | ² = 1. Donc, à la mesure, on trouve avec probabilité de α² et , avec une probabilité de β². Surviennent ainsi les questions de mesure quantique, de distinction des états quantiques et de mesure projective.

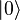
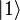
Il y a plusieurs façons physiques de représenter un qubit. Parmi celles-ci :

• spin d'électron
• niveaux d'énergie dans un atome
• polarisation d'un photon