Inharmonicité du piano - Définition

Introduction

Les cordes de piano sont des cordes filées dans le grave et des fils d'acier de diamètre relativement important dans le médium et dans l'aigu. Ces fils d'acier, du fait de leur raideur, ont une inharmonicité d'autant plus grande que la corde est plus courte (leur partiel n° 2 est à une fréquence un peu plus grande que 2 fois leur fondamental). Lorsque l'accordeur de piano reporte la partition qu'il vient de réaliser sur l'octave initiale en l'étendant à tout le clavier aux moyen d'octaves sans battements, les octaves ont un rapport de fréquence supérieur au rapport 2/1, dans l'aigu d'une part (où les cordes sont de trop gros diamètre par rapport à leur longueur) et dans l'extrême grave d'autre part (où les cordes filées, bien que plus souples que des cordes monofilaments, ne sont pas assez longues par rapport à ce qu'il faudrait pour doubler leur longueur à chaque descente d'octave).

On examine ici le rôle de l'inharmonicité dans l'accordage du piano (les calculs de physique sont donnés en annexe) et les problèmes de justesse que l'on rencontre quand d'autres instruments jouent avec un piano (en musique de chambre ou en orchestre).

Terminologie utilisée ci-dessous : sens de pure, sans battement, juste

On constate que des terminologies différentes sont utilisées pour désigner les mêmes choses et que, à l'inverse, le même terme est utilisé pour désigner des choses différentes, Dans ce qui suit, la terminologie employée sera la suivante :

• pure ou pur sera réservé aux intervalles fondés sur des rapports harmoniques (octave pure pour un rapport de fréquence de 2, quinte pure pour un rapport de fréquences de 3/2, tierce majeure pure pour un rapport de fréquences de 5/4).
• sans battement sera réservé aux intervalles résultant de l'accord de cordes réelles, compte tenu de leur inharmonicité (octave sans battement pour l'accord décrit plus haut).
• juste sera réservé aux problèmes de justesse musicale (problèmes à résoudre afin qu'un ou plusieurs musiciens, dans un contexte donné, jouent juste).

Plan de cordes d'un piano de concert

La qualité d'un piano de concert tient à la réussite d'un grand nombre de points de facture qui conditionnent la qualité du son et la précision du mécanisme, dont dépend le toucher. Parmi tous ces points, le plan de cordes joue un rôle important, qui sera décisif au moment de l'accord du piano. Le plan de cordes définit leur longueur, leur diamètre, leur tension et leur facture. La facture (technologie de fabrication) est importante pour les cordes filées, elle se résume à la métallurgie pour les cordes monofilaments.

Réussite d'un plan de cordes

La réussite d'un plan de corde tient, pour beaucoup, à la régularité de la progression de l'inharmonicité d'une corde à la suivante. En effet, toute rupture dans la régularité de cette progression se traduira inévitablement par un écart notable de couleur entre deux notes consécutives, défaut très vite repéré par les musiciens, qui rendrait l'instrument inacceptable.

Le problème est examiné en détail dans le livre de Jean Lattard.

La réussite est d'autant plus difficile qu'il faut passer des cordes filées, nécessaires dans le grave aux cordes monofilaments, passer d'une corde à deux, puis à trois. Il faut, de plus, franchir des barres du cadre, qui imposent des variations de longueur, sans que cela s'entende. Il faut enfin régler le volume sonore des différentes tessitures en jouant sur des ajustements de la tension : si la tension reste toujours comprise entre 60 et 75 kg pour chaque corde, les diamètres sont ajustés de sorte que la tension soit plus grande dans certaines tessitures et moins grande dans d'autres (voir Jean Lattard p. 231). Un piano de concert tel que le Steinway étudié par Jean Lattard (piano de 1890, restauré en 1991) utilise pour ses cordes monofilament 10 diamètres finement échelonnés (de 1,025 à 0,800 mm).

Progression de l'inharmonicité et de la dilatation des octaves

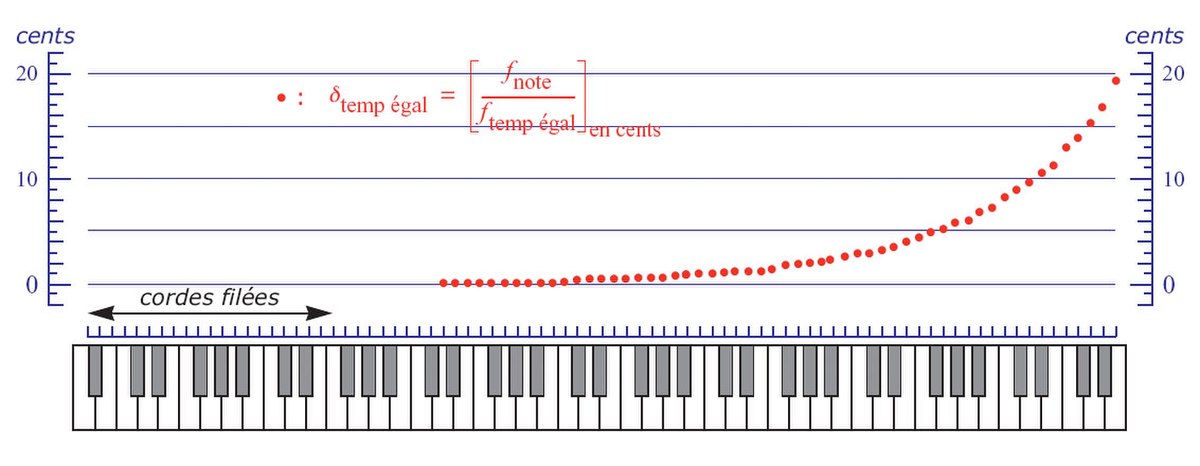
Une fois le piano soigneusement accordé, la fréquence de chaque note, précisément mesurée, donnée par Jean Lattard (dans deux tableaux pp. 233 et 234), peut être comparée à la fréquence qu'aurait la même note dans le tempérament égal avec le la à 440Hz.

Relevé d'accord d'un piano Steinway : pour chaque note de la partie supérieure du plan des cordes, écart de la fréquence mesurée à la fréquence qu'elle aurait au tempérament égal (la : 440 Hz).

On constate que le piano n'est pas du tout accordé au tempérament égal, contrairement à ce que l'on dit souvent, du moins au tempérament égal au sens d'un accordeur électronique (avec des octaves au rapport 2/1). Dans la partie supérieure du plan des cordes, l'écart au tempérament égal est d'autant plus important qu'on monte plus haut dans l'aigu du piano. Dans le registre bas médium et médium, les cordes ont très peu de raideur, les partiels sont pratiquement harmoniques, il ne faut pas dilater les octaves. Dans l'aigu, à partir de 1 000 Hz, on sait qu'un son pauvre en harmoniques sonne trop bas (voir : Échelle de Mel) : remonter les fréquences de l'aigu du piano n'est pas, pour cette raison, psychoacoustiquement gênant. Un piano qui serait accordé au tempérament égal sonnerait faux, particulièrement dans l'aigu.

Pour les graves (partie inférieure du plan des cordes), Daniel Magne écrit :

« Enfin, il importe, pour les graves, de s'attacher principalement à l'exactitude parfaite des unissons en octaves, afin d'obtenir le ronflement cumulé des fréquences parfaitement ajustées qui donnent à l'instrument la profondeur et l'amplitude de ce registre. »

L'accordeur de piano tient compte, lorsqu'il écoute les battements, du fait que le partiel deux de chaque corde est plus haut que deux fois le fondamental de cette corde, ce qui conduit à dilater les octaves quand il reporte la partition initiale. Ceci apparaît d'une façon nette lorsque l'on compare l'intervalle du partiel deux au partiel un d'une corde avec l'intervalle de cette note à la note correspondante de l'octave immédiatement supérieure.

Inharmonicité calculée pour toute la partie supérieure du plan des cordes d'un piano Steinway. En bleu : rapport calculé des fréquences du partiel 2 au partiel 1 pour chaque corde (inharmonicité). En rouge : calcul de l'intervalle d'octave des notes, à partir des fréquences mesurées pour toutes les notes sur le piano accordé.

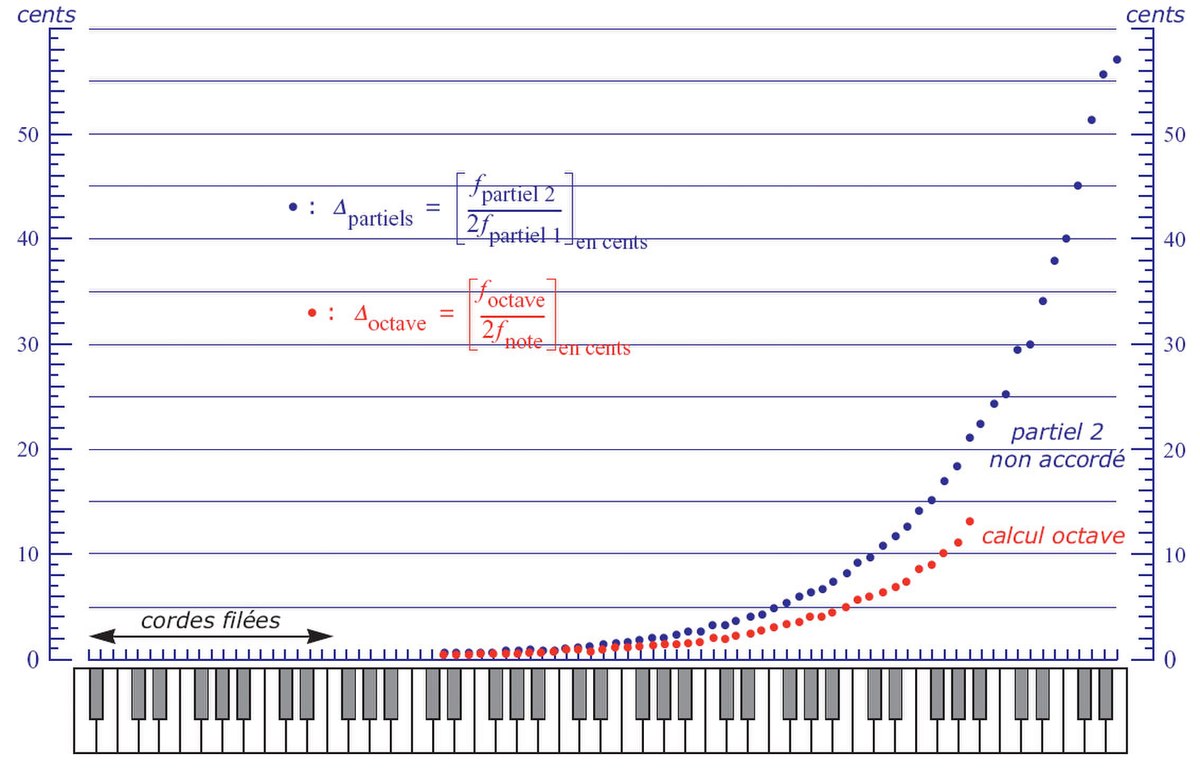
Remarques sur l'accord

Alors que la ressemblance entre les courbes en rouge et en bleu de la figure ci-dessus est patente, il convient de remarquer que ces deux courbes concernent des domaines a priori très différents. La courbe en bleu concerne la couleur sonore de chaque note (rapport de fréquence de deux partiels) alors que la courbe en rouge concerne l'accord du piano (justesse des octaves au clavier). Cette ressemblance traduit le fait que, pour que le piano sonne bien, il faut qu'il soit accordé en tenant compte de la couleur sonore de chaque corde, qui varie d'une corde à l'autre et d'un piano à l'autre.

Ceci va à l'encontre de l'idée qu'on pourrait plaquer une échelle universelle de hauteurs, qui serait la même pour tous les pianos, telle le Tempérament égal à quintes justes promu par Serge Cordier^{[citation nécessaire]}. Dans une telle échelle, la dilatation des octaves, censée être la même sur toute l'étendue du clavier, serait trop petite dans l'aigu et trop grande dans le médium et le bas médium (voir mesures du Ré2 au La6). De plus, cette échelle ne pourrait être réalisée qu'à l'accordeur électronique : en effet, une quinte accordée sans battements n'est aucunement une quinte pure, puisque les battements concernent le partiel 3 d'une note de la quinte et le partiel 2 de l'autre note, partiels tous deux affectés par l'inharmonicité des cordes. Un piano accordé par quintes sans battements n'est donc aucunement accordé suivant l'échelle universelle du tempérament égal à quintes pures ^{[réf. souhaitée]} : les quintes y sont d'autant plus dilatées que les cordes sont plus inharmoniques, elles sont d'autant moins pures que l'on va davantage dans l'aigu.

L'oreille, de la même façon qu'elle reconstitue la fondamentale d'une note basse de piano à partir des harmoniques audibles (la table d'harmonie est trop petite pour résonner au niveau du premier ou des deux premiers partiels), doit certainement entendre l'addition de tous les partiels plus la fondamentale comme un tout, produisant alors un son perçu comme ayant une certaine hauteur. L'accordeur qui n'écoute la justesse que par rapport à des battements de partiels ne cherche pas à obtenir la résonance naturelle du piano. Celui qui se base sur le timbre de l'instrument et l'acoustique de la pièce déterminera (empiriquement) un type d'étirement de l'accord adapté au lieu, mais aussi éventuellement à la musique jouée, aux autres instruments, etc.

Chaque piano a sa justesse propre, sur laquelle l'accordeur plaque sa façon d'appréhender la justesse avec plus ou moins de respect des résonances intrinsèques et naturelles de celui-ci.