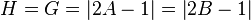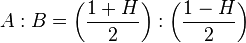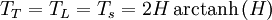Loi de Pareto - Définition
La liste des auteurs de cet article est disponible ici.
Utilisation dans la méthode six sigma
Le diagramme de Pareto est utilisé dans l'approche Six Sigma pour résumer et afficher graphiquement l'importance relative des différences entre groupes de données. Ce diagramme est construit en segmentant les données en groupes (aussi appelés segments ou catégories), le côté gauche de l'axe vertical du diagramme de Pareto contient le nombre d'instances pour chaque catégorie, le côté droit est le pourcentage cumulatif. L'axe horizontal représente les noms des catégories.
Utilisation en gestion
La loi de Pareto n’est pas toujours dictée par la seule recherche de la facilité : le fait que 20 % des moyens permettent d’atteindre 80 % des objectifs formalise un acte de gestion raisonné, inscrit dans la durée.
La loi de Pareto remplace essentiellement une « distribution linéaire », quand celle-ci ne répond pas à l'observation, par une autre proposant une distribution moins uniforme, moins linéaire.
- La gestion ne se réduit pas au contrôle de gestion, mais consiste fondamentalement à décoder et accompagner les faits, et c’est à cela qu’aide la loi de Pareto, en suggérant de se concentrer au début sur le petit nombre de faits qui va expliquer le plus de choses (Loi des rendements décroissants).
- Gestion de production : lorsqu’une distribution linéaire est obtenue (production, sondages, phénomènes physique, problèmes à traiter, etc.), alors, les coûts de gestion sont optimisés.
- Gestion des risques : lorsque 80 % des articles restant sont ramenés à des niveaux raisonnables, alors, la pérennité de l’entreprise est assurée.
Autres domaines
La loi de Pareto est aussi utilisée en :
- mathématiques : distribution de Pareto
- électronique : pour diminuer les nuisances sonores d’un circuit (source Esinsa 2005)
- sociologie : pour cerner une problématique difficile et la rendre gérable (site 2rh 2005)
- ergonomie : pour concevoir des interfaces utilisateurs simple d'accès (en règle générale, 20 % des fonctionnalités sont utilisées 80 % du temps)
Mesures d'inégalité
Pour le format “A:B” (exemple : 0,8:0,2) et A + B = 1 la formule pour le coefficient de Gini et l´indice de Hoover est :
La formule pour l'indice de Theil:
Critique
Bien que la loi de Pareto soit remarquablement vérifiée tout au long du XXe siècle pour les hauts revenus, l'éconophysique contredit aujourd'hui ses conclusions en matière d'impôts sur le revenu et le capital.
Exemples d'applications de la loi des 80/20
- GENERAL :
- 20% des causes provoquent 80% des effets ;
- 20% des problèmes représentent 80% des préoccupations ;
- ACCOMPLISSEMENT :
- 20% des facteurs influent sur 80% des objectifs ;
- 20% des moyens permettent d'atteindre 80% des objectifs ;
- 20% du temps de travail suffit à accomplir 80% d'une tâche ;
- 20% du personnel assure 80% du travail ;
- 20% de votre activité fournit 80% de vos résultats ;
- 80% d'accomplissement d'une mise au point nécessite 20% de l'effort en gestion de projets ;
- 80% d'une production résulte de 20% de l'investissement qui lui a été consacré ;
- RESSOURCES :
- 20% des gens possèdent 80% des richesses ;
- 20% de la population mondiale a accès à 80% de l'eau potable ;
- 20% des salariés perçoivent 80% de la masse salariale ;
- 20% de la population mondiale tire profit de 80% des ressources globales de la planète ;
- COMMERCE :
- 20% des produits représentent 80% du chiffre d'affaires ;
- 20% des ventes représentent 80% de la marge bénéficiaire ;
- 20% de l'inventaire représente 80% de la valeur du stock ;
- 20% des fournisseurs représentent 80% du volume d'achat total ;
- 20% des entreprises réalisent 80% du PIB ;
- 80% du chiffre d'affaires est réalisé avec seulement 20% des clients ;
- 80% du chiffre d'affaires est réalisé par 20% des commerciaux ;
- DEFAILLANCES :
- 20% des clients sont à l'origine de 80% des réclamations ;
- 20% du personnel est concerné par 80% des accidents du travail ;
- 20% des défaillances de production sont à l'origine de 80% des défauts des produits ;
- 20% des défauts du matériel sont à l'origine de 80% des défaillances à l'utilisation ; (ces deux assertions mises bout à bout permettent de comprendre le caractère hyperbolique de cette loi !)
- 20% des automobilistes causent 80% des accidents ;
- INFORMATION :
- 20% des indicateurs fournissent 80% de l'information de gestion ;
- 20% seulement des documents archivés apportent 80% de l'information utile ;
- 20% des e-mails reçus apportent 80% de l'information utile ;
- 20% des lecteurs lisent 80% des livres vendus ;
- 20% des mots dans une langue suffisent pour s'exprimer dans 80% des cas ;
- 20% des pages de Wikipédia sont consultées par 80% des Wikinautes ;
- CONSOMMATION :
- ECOLE :
- 20% des élèves produisent 80% des perturbations dans la classe ;
- 20% des élèves d'une classes font 80% de la participation utile ; (cf. exemples sur intelligence et bêtise humaine ...)
- 20% des étudiants demandent 80% de l'énergie de leur enseignant ;
- 20% du temps d'apprentissage est consacré à 80% de ce qu’il faut savoir de votre leçon ;
- SOCIETE :
- 20% des hommes politiques détiennent 80% de l'espace débat ;
- 20% des délinquants génèrent 80% des délits ;
- 80% de l'intelligence humaine est le fruit de 20% des humains ;
- 80% de la bêtise humaine est le produit de 20% du genre humain ; (moralité : 60% de l'humanité constitue donc une majorité moyenne qui ne se distingue d'aucune façon ... ;)
- 20% des députés font voter 80% des lois ;
- 20% des noms de familles sont portés par 80% des habitants ;
- 20% des citoyens imposables génèrent 80% de la trésorerie publique ;
- INFORMATIQUE :
- 20% du jeu d'instructions d'un microprocesseur est utilisé 80% du temps de calcul ;
- SPORT :
- 20% de l'effort à l'entrainement permet d'atteindre 80% de la performance pour un sportif ;
- 20% des joueurs de foot marquent 80% des buts ; (attention : voir en discussion)
- EMPLOI DU TEMPS :
- Vous consacrez 80% de votre temps à 20% de vos activités
- Vous consacrez 80% de votre temps libre à 20% de vos loisirs