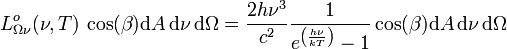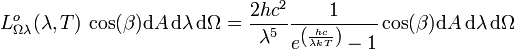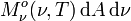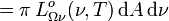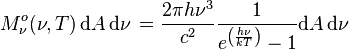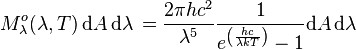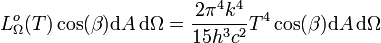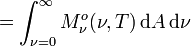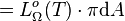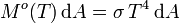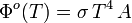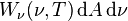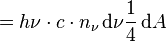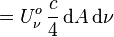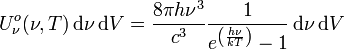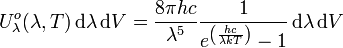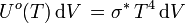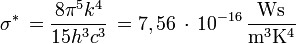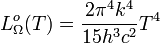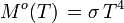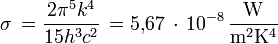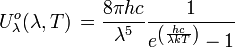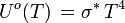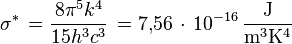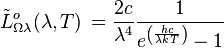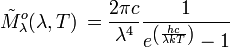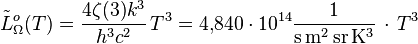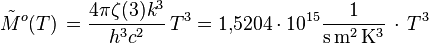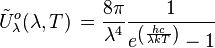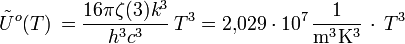Mardi 29 Avril 2025
Rechercher 🔍

Loi de Planck - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Introduction - Conséquences - Description - Répartition de l'intensité du rayonnement du corps noir - Lois de rayonnement et hypothèse quantique

Description

Comme la loi de Planck est valable dans de nombreux contextes différents, elle s'exprime sous différentes formes, toutes dérivées les unes des autres. Pour comprendre ces différentes formes de la loi de Planck, nous allons d'abord énoncer les grandeurs qui apparaissent dans les différentes formules.

Comme il est d'usage pour les grandeurs radiométriques, différentes grandeurs de rayonnement peuvent être utilisées pour décrire le spectre du rayonnement d'un corps noir. Les dénominations et symboles utilisés ici suivent la norme ISO 9288 (Août 1996). L'indice haut \,^o indique que la grandeur en question décrit spécifiquement les propriétés d'un corps noir. Les formules suivantes sont valables pour le rayonnement dans le vide. Pour le rayonnement dans un milieu d'indice de réfraction n, il faut remplacer les célérités dans le vide c par c/n et les longueurs d'onde λ par λ/n, sans modifier la fréquence ν.

On différencie

  • les grandeurs spectrales, qui décrivent la dépendance à la fréquence (ou à la longueur d'onde) de manière explicite,
  • les grandeurs totales, intégrées sur l'ensemble des fréquences (ou des longueurs d'onde)

ainsi que

  • les grandeurs directionnelles, qui décrivent la dépendance à la direction de manière explicite,
  • les grandeurs hémisphériques, intégrées sur toutes les directions du demi-espace.

Luminance energétique monochromatique

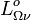
La luminance énergétique monochromatique L^o_{\Omega\nu} d'un corps noir à la température absolue T vaut

  • Selon la fréquence :
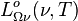
L^o_{\Omega\nu}(\nu, T) \, \cos(\beta)\mathrm{d}A \, \mathrm{d}\nu \, \mathrm{d}\Omega = \frac{2 h\nu^{3}}{c^2} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1}\cos(\beta)\mathrm{d}A \, \mathrm{d}\nu \, \mathrm{d}\Omega

Unité SI de L^o_{\Omega\nu}(\nu, T)  : W m-2 Hz-1 sr-1,

  • Selon la longueur d'onde :
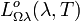
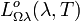
L^o_{\Omega\lambda}(\lambda, T) \, \cos(\beta)\mathrm{d}A \, \mathrm{d}\lambda \, \mathrm{d}\Omega = \frac{2 h c^2}{\lambda^5} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}\cos(\beta)\mathrm{d}A \, \mathrm{d}\lambda \, \mathrm{d}\Omega

Unité SI de L^o_{\Omega\lambda}(\lambda, T)  : W m-2 m-1 sr-1.


L^o_{\Omega\lambda}(\lambda, T) est la puissance rayonnée par un élément de surface dA dans le domaine de fréquences entre ν et ν+dν, dans l'élement d'angle solide dΩ délimité par les angles azimutaux φ et φ+dφ ainsi que les angles d'ascension polaires β et β+dβ. h est la constante de Planck, c est la célérité de la lumière dans le vide et k est le constante de Boltzmann. Le facteur cos(β) prend en compte le fait que, pour le rayonnement dans une direction indiquée par φ et β, seule la projection orthogonale à cette direction cos(β)dA de la surface dA est prise en compte comme surface rayonnante effective.

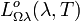
La luminance énergétique monochromatique L^o_{\Omega\lambda}(\lambda, T) doit être indépendante de la direction pour des raisons thermodynamiques.

Le corps noir rayonne de manière totalement diffuse, et suit le modèle du rayonnement de Lambert.

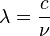
Lors du passage entre représentation fréquentielle et représentation en longueur d'onde, comme \lambda = \frac{c}{\nu} , on a les relations :

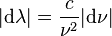
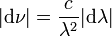
|\mathrm{d}\lambda| = \frac{c}{\nu^2} |\mathrm{d}\nu| et |\mathrm{d}\nu| = \frac{c}{\lambda^2} |\mathrm{d}\lambda|

La luminance énergétique monochromatique est, comme son nom l'indique, une grandeur spectrale.

Exitance energétique monochromatique

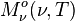
En intégrant la luminance énergétique monochromatique suivant toutes les directions du demi-espace dans lequel rayonne l'élément de surface étudié, on obtient l'exitance energétique monochromatique M^o_\nu(\nu, T) . Il vient :

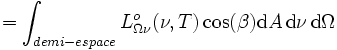
M^o_\nu(\nu, T) \, \mathrm{d}A \, \mathrm{d}\nu = \int_{demi-espace} L^o_{\Omega\nu}(\nu, T) \cos(\beta)\mathrm{d}A \, \mathrm{d}\nu \, \mathrm{d}\Omega
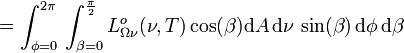
= \int_{\phi=0}^{2\pi} \, \int_{\beta=0}^{\frac{\pi}{2}} L^o_{\Omega\nu}(\nu, T) \cos(\beta)\mathrm{d}A \, \mathrm{d}\nu \, \sin(\beta) \, \mathrm{d}\phi \, \mathrm{d}\beta
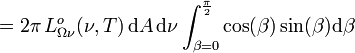
= 2\pi \, L^o_{\Omega\nu}(\nu, T) \, \mathrm{d}A \, \mathrm{d}\nu \int_{\beta=0}^{\frac{\pi}{2}} \cos(\beta) \sin(\beta) \mathrm{d}\beta
= \pi \, L^o_{\Omega\nu}(\nu, T) \, \mathrm{d}A \, \mathrm{d}\nu ,

soit :

  • Selon la fréquence
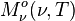
M^o_{\nu}(\nu, T) \, \mathrm{d}A \, \mathrm{d}\nu \, = \frac{2\pi h\nu^{3}}{c^2} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1}\mathrm{d}A \, \mathrm{d}\nu

Unité SI de M^o_{\nu}(\nu, T)  : W m-2 Hz-1

  • Selon la longueur d'onde
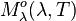
M^o_{\lambda}(\lambda, T) \, \mathrm{d}A \, \mathrm{d}\lambda \, = \frac{2\pi h c^2}{\lambda^5} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}\mathrm{d}A \, \mathrm{d}\lambda

Unité SI de M^o_{\lambda}(\lambda, T)  : W m-2 m-1.


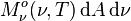
M^o_{\nu}(\nu, T) \, \mathrm{d}A \, \mathrm{d}\nu est la puissance rayonnée par l'élément de surface dA dans le domaine de fréquences entre ν et ν+dν dans le demi-espace. L'exitance énergétique monochromatique est une grandeur spectrale hémisphérique.

Luminance énergétique

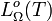
En intégrant la luminance énergétique monochromatique non pas sur les directions mais sur les fréquences, on obtient la luminance énergétique (totale) L^o_{\Omega}(T) , telle que :

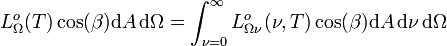
L^o_{\Omega}(T) \cos(\beta)\mathrm{d}A \, \mathrm{d}\Omega = \int_{\nu=0}^{\infty} L^o_{\Omega\nu}(\nu, T) \cos(\beta)\mathrm{d}A \, \mathrm{d}\nu \, \mathrm{d}\Omega

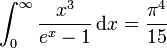
Comme \int_{0}^{\infty} \frac{x^3}{e^{x}-1} \, \mathrm{d}x = \frac{\pi^4}{15} , le calcul de l'intégrale donne :

L^o_{\Omega}(T) \cos(\beta)\mathrm{d}A \, \mathrm{d}\Omega = \frac{2 \pi^4 k^4}{15 h^3 c^2} T^4 \cos(\beta)\mathrm{d}A \, \mathrm{d}\Omega

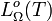
Unité SI de L^o_{\Omega}(T)  : W m-2 sr-1.


est la puissance rayonnée par l'élément de surface dA sur toutes les fréquences dans l'angle solide dans la direction donnée par β.

La luminance énergétique est une grandeur totale directionnelle.

Exitance énergétique, densité de flux radiatif, loi de Stefan-Boltzmann

(voir l'article Loi de Stefan-Boltzmann)

En intégrant l'exitance énergétique monochromatique sur toutes les fréquences ou bien la luminance énergétique sur toutes les directions du demi-espace, on obtient l'exitance énergétique (ou densité de flux radiatif) Mo(T), telle que :

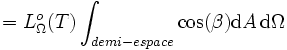
M^o(T) \, \mathrm{d}A = \int_{\nu=0}^{\infty} M^o_{\nu}(\nu, T) \, \mathrm{d}A \, \mathrm{d}\nu = L^o_{\Omega}(T) \int_{demi-espace} \cos(\beta)\mathrm{d}A \, \mathrm{d}\Omega
= L^o_{\Omega}(T) \cdot \pi \mathrm{d}A

soit

M^o(T) \, \mathrm{d}A = \sigma \, T^4 \, \mathrm{d}A

Unité SI de Mo(T) : W m-2,

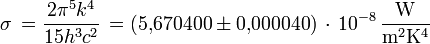
avec la constante de Stefan-Boltzmann \sigma \, = \frac{2 \pi ^5 k^4}{15 h^3 c^2} \, = (5{,}670 400 \pm 0{,}000 040) \, \cdot \, 10^{-8} \, \mathrm{\frac{W}{m^2 K^4}} (CODATA 2000).

Pour le rayonnement dans un milieu d'indice de réfraction n, la célérité de la lumière c doit être remplacée par c/n. L'exitance energétique augmente donc d'un facteur n2.

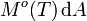
M^o(T) \, \mathrm{d}A est la puissance rayonnée par l'élément de surface dA sur toutes les fréquences dans le demi-espace.

L'exitance énergétique est une grandeur totale hémisphérique.

Flux radiatif

En intégrant l'exitance énergétique (densité de flux radiatif), sur l'ensemble de la surface rayonnante A, on obtient le flux radiatif (ou puissance rayonnée) de cette surface Φo(T), pour laquelle :

\Phi^o(T) = \int_{\rm Surface} M^o(T) \, \mathrm{d}A ,

soit

\Phi^o(T) = \sigma \, T^4 \, A

Unité SI de Φo(T) : W.


Φo(T) est la puissance rayonnée par l'ensemble de la surface A sur toutes les fréquences et dans le demi-espace tout entier.

Densité spectrale d'énergie du rayonnement d'une cavité à rayonnement isotrope

Considérons une cavité fermée, dont les parois sont composées d'un matériau quelconque, et maintenu à la température T. A l'équilibre thermique, la cavité est emplie d'un rayonnement thermique isotrope, dont les caractéristiques ne dépendent que de la température T, et qui a donc un caractère universel.

En insérant un corps noir dans cette cavité, le rayonnement de la cavité doit redevenir identique après avoir atteint l'équilibre thermique, puisque le rayonnement ne dépend que de la température T. Comme le corps noir absorbe une certaine quantité de rayonnement et doit en émettre la même quantité au même moment pour garantir l'équilibre, les luminances énergétiques spectrales de la cavité et le rayonnement du corps noir doivent être identiques. Les expression des grandeurs obtenues ci-dessus sont donc également valables pour le rayonnement de la cavité, et celui-ci a une énergie volumique de rayonnement constante, comme nous allons le voir.

Considérons une calotte sphérique emplie d'un rayonnement de corps creux dû à la température T. Comme les grandeurs de rayonnement sont les mêmes que pour le rayonnement du corps noir, la puissance incidente sur un élément de surface dA au centre du disque sur lequel repose la calotte, provenant de l'ensemble de la calotte sphérique, et dans le domaine de fréquences de ν à ν+dν, est donnée par la formule de l'exitance énergétique spectrale :

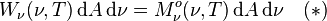
W_{\nu}(\nu, T)\, \mathrm{d}A \, \mathrm{d}\nu = M^o_\nu(\nu, T) \, \mathrm{d}A \, \mathrm{d}\nu \quad (*)

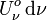
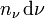
Soit U^o_{\nu} \, \mathrm{d}\nu la densité d'énergie dans l'intervalle de fréquences de ν à ν+dν, et n_{\nu} \, \mathrm{d}\nu la densité de photons dans le même intervalle de fréquences :

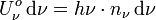
U^o_{\nu} \, \mathrm{d}\nu = h \nu \cdot n_{\nu} \, \mathrm{d}\nu

Comme le rayonnement est isotrope, la quantité de photons provenant de l'angle solide dΩ (donc de directions entre φ et φ+dφ et entre β et β+dβ) est donnée par le rapport de dΩ à l'angle solide de l'espace tout entier 4π. La densité de photons de fréquence entre ν et ν+dν provenant de l'angle solide dΩ est donc :

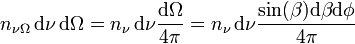
n_{\nu \Omega} \, \mathrm{d}\nu \, \mathrm{d}\Omega = n_{\nu} \, \mathrm{d}\nu \frac{\mathrm{d}\Omega}{4\pi} = n_{\nu} \, \mathrm{d}\nu \frac{\sin(\beta) \mathrm{d}\beta \mathrm{d}\phi}{4\pi}


Parmi tous les photons de l'intervalle dν provenant de la direction dΩ, certains atteignent une surface dA se trouvant dans un cylindre penché β d'un angle dans la direction de dΩ et de surface de base dA. Par unité de temps dt, les photons qui traversent dA sont ceux qui se trouvent dans le cylindre de longueur cdt. Ils traversent donc dA avec un taux :

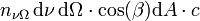
n_{\nu \Omega} \, \mathrm{d}\nu \, \mathrm{d}\Omega \cdot \cos(\beta)\mathrm{d}A \cdot c

Comme chaque photon a une énergié hν, l'énergie traversant dA par unité de temps vaut :

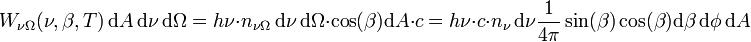
W_{\nu \Omega}(\nu, \beta, T) \, \mathrm{d}A \, \mathrm{d}\nu \, \mathrm{d}\Omega = h \nu \cdot n_{\nu \Omega} \, \mathrm{d}\nu \, \mathrm{d}\Omega \cdot \cos(\beta)\mathrm{d}A \cdot c = h \nu \cdot c \cdot n_{\nu} \, \mathrm{d}\nu \frac{1}{4\pi} \sin(\beta) \cos(\beta) \mathrm{d}\beta \, \mathrm{d}\phi \, \mathrm{d}A

Des photons provenant de l'ensemble de la calotte sphérique traversent dA. L'intégration sur l'ensemble du demi-espace donne :

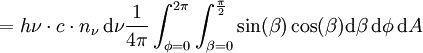
W_{\nu}(\nu, T) \, \mathrm{d}A \, \mathrm{d}\nu = h \nu \cdot c \cdot n_{\nu} \, \mathrm{d}\nu \frac{1}{4\pi} \int_{\phi=0}^{2\pi} \int_{\beta=0}^{\frac{\pi}{2}} \sin(\beta) \cos(\beta) \mathrm{d}\beta \, \mathrm{d}\phi \, \mathrm{d}A
= h \nu \cdot c \cdot n_{\nu} \, \mathrm{d}\nu \frac{1}{4} \, \mathrm{d}A
= U^o_{\nu} \, \frac{c}{4} \, \mathrm{d}A \, \mathrm{d}\nu

La comparaison avec ( * ) fait apparaître la relation :

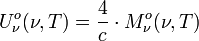
U^o_{\nu}(\nu, T) = \frac{4}{c} \cdot M^o_\nu(\nu, T)

On a donc :

  • Selon la fréquence :
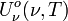
U^o_{\nu}(\nu, T) \, \mathrm{d}\nu \, \mathrm{d}V = \frac{8 \pi h \nu^{3}}{c^3} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1} \, \mathrm{d}\nu \, \mathrm{d}V

Unité SI de U^o_{\nu}(\nu, T)  : J m-3 s ou bien J m-3 Hz-1,

  • Selon la longueur d'onde :
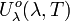
U^o_{\lambda}(\lambda, T) \, \mathrm{d}\lambda \, \mathrm{d}V = \frac{8 \pi h c}{\lambda^5} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1} \, \mathrm{d}\lambda \, \mathrm{d}V

Unité SI de U^o_{\lambda}(\lambda, T)  : J m-4 ou bien J m-3 m-1.

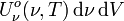
U^o_{\nu}(\nu, T) \, \mathrm{d}\nu \, \mathrm{d}V est l'énergie du rayonnement thermique dans le domaine de fréquence de ν à ν+dν qui se trouve dans le volume élémentaire dV de la cavité rayonnante.

Densité totale d'énergie du rayonnement d'une cavité à rayonnement isotrope

En intégrant la densité spectrale d'énergie du rayonnement d'une cavité rayonnante sur toutes les fréquences, on obtient la densité totale d'énergie du rayonnement de la cavité à rayonnement isotrope Uo :

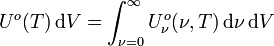
U^o(T) \, \mathrm{d}V = \int_{\nu=0}^{\infty}U^o_{\nu}(\nu, T) \, \mathrm{d}\nu \, \mathrm{d}V

Le calcul de l'intégrale donne :

U^o(T) \, \mathrm{d}V \, = \sigma^* \, T^4 \, \mathrm{d}V
avec \sigma^* \, = \frac{8 \pi ^5 k^4}{15 h^3 c^3} \, = 7,56 \, \cdot \, 10^{-16} \, \mathrm{\frac{W s}{m^3 K^4}} , Unité SI de Uo(T) : J m-3.

U^o(T) \, \mathrm{d}V est l'énergie du rayonnement thermique de toutes les fréquences se trouvant dans le volume dV de la cavité.

Formulaire

Luminance énergétique spectrale :
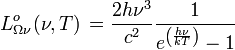
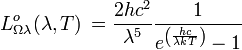
L^o_{\Omega\nu}(\nu, T) \, = \frac{2 h\nu^{3}}{c^2} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1} L^o_{\Omega\lambda}(\lambda, T) \, = \frac{2 h c^2}{\lambda^5} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}
Unité : W m-2 Hz-1 sr-1 Unité : W m-2 m-1 sr-1
 
Émittance énergétique spectrale :
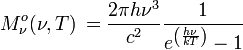
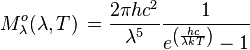
M^o_{\nu}(\nu, T) \, = \frac{2 \pi h\nu^{3}}{c^2} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1} M^o_{\lambda}(\lambda, T) \, = \frac{2 \pi h c^2}{\lambda^5} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}
Unité : W m-2 Hz-1 Unité : W m-2 m-1
 
Luminance énergétique :
L^o_{\Omega}(T) = \frac{2 \pi^4 k^4}{15 h^3 c^2} T^4
Unité : W m-2 sr-1
 
Émittance énergétique (loi de Stefan-Boltzmann):
M^o(T) \, = \sigma \, T^4 avec constante de Stefan-Boltzmann \sigma \, = \frac{2 \pi ^5 k^4}{15 h^3 c^2} \, = 5{,}67 \, \cdot \, 10^{-8} \, \mathrm{\frac{W}{m^2 K^4}}
Unité : W m-2
 
Densité spectrale d'énergie d'une cavité à rayonnement isotrope :
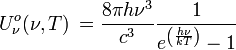
U^o_{\nu}(\nu, T) \, = \frac{8 \pi h \nu^{3}}{c^3} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1} U^o_{\lambda}(\lambda, T) \, = \frac{8 \pi h c}{\lambda^5} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}
Unité : J m-3 Hz-1 Unité : J m-3 m-1
 
Densité totale d'énergie d'une cavité à rayonnement isotrope :
U^o(T) \, = \sigma^* \, T^4 avec \sigma^* \, = \frac{8 \pi ^5 k^4}{15 h^3 c^3} \, = 7{,}56 \, \cdot \, 10^{-16} \, \mathrm{\frac{J}{m^3 K^4}}
Unité : J m-3

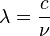
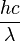
On peut considérer le nombre de photons émis par unité de temps, plutôt que l'énergie rayonnée. Comme un photon de fréquence ν (ou de longueur d'onde \lambda = \frac{c}{\nu} ) a une énergie hν (ou \frac{hc}{\lambda} ) on a :

Luminance énergétique spectrale :
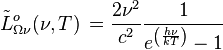
\tilde L^o_{\Omega\nu}(\nu, T) \, = \frac{2 \nu^{2}}{c^2} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1} \tilde L^o_{\Omega\lambda}(\lambda, T) \, = \frac{2 c}{\lambda^4} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}
Unité : Photons s-1 m-2 Hz-1 sr-1 Unité : Photons s-1 m-2 μm-1 sr-1
 
Émittance energétique spectrale :
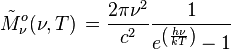
\tilde M^o_{\nu}(\nu, T) \, = \frac{2 \pi \nu^{2}}{c^2} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1} \tilde M^o_{\lambda}(\lambda, T) \, = \frac{2 \pi c}{\lambda^4} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}
Unité : Photons s-1 m-2 Hz-1 Unité : Photons s-1 m-2 μm-1
 
Luminance énergétique :
\tilde L^o_{\Omega}(T) = \frac{4 \zeta(3) k^3}{h^3 c^2}\, T^3 = 4{,}840 \cdot 10^{14} \mathrm{\frac{1}{s \, m^2 \, sr \, K^3}} \, \cdot \, T^3
avec ζ(3) = 1,202056903... (constante d'Apéry où ζ désigne la fonction zêta de Riemann)
Unité : Photons s-1 m-2 sr-1
 
Excitance énergétique (loi de Stefan-Boltzmann pour le taux de photons) :
\tilde M^o(T) \, = \frac{4 \pi \zeta(3) k^3}{h^3 c^2}\, T^3 = 1{,}5204 \cdot 10^{15} \mathrm{\frac{1}{s \, m^2 \, K^3}} \, \cdot \, T^3
Unité : Photons s-1 m-2
 
Densité spectrale de photons d'une cavité à rayonnement isotrope :
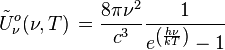
\tilde U^o_{\nu}(\nu, T) \, = \frac{8 \pi \nu^{2}}{c^3} \frac{1}{e^{\left(\frac{h\nu}{kT}\right)}-1} \tilde U^o_{\lambda}(\lambda, T) \, = \frac{8 \pi}{\lambda^4} \frac{1}{e^{\left(\frac{hc}{\lambda kT}\right)}-1}
Unité : Photons m-3 Hz-1 Unité : Photons m-3 μm-1
 
Densité totale de photons d'une cavité à rayonnement isotrope :
\tilde U^o(T) \, = \frac{16 \pi \zeta(3) k^3}{h^3 c^3}\, T^3 = 2{,}029 \cdot 10^{7} \, \mathrm{\frac{1}{m^3 K^3}} \, \cdot \, T^3
Unité : Photons m-3
Conséquences
Répartition de l'intensité du rayonnement du corps noir
- Introduction - Introduction - Conséquences - Description - Répartition de l'intensité du rayonnement du corps noir - Lois de rayonnement et hypothèse quantique
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
Page générée en 0.140 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise