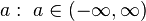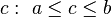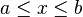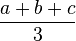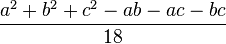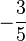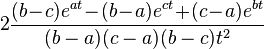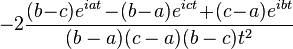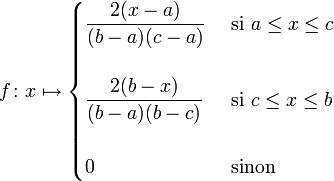Loi triangulaire - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Introduction
En théorie des probabilités, une loi triangulaire est une loi de probabilité dont la fonction de densité est affine de son minimum à son mode et de son mode à son maximum. Elle est mentionnée sous deux versions : une loi discrète et une loi continue.
Version discrète
La loi triangulaire discrète de paramètre entier positif a est définie pour tout entier x compris entre − a et a par :
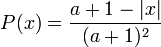
Version continue
| Triangulaire | |
|---|---|
| |
| |
| | |
| Paramètres |
 |
| Support |
|
| Densité de probabilité (fonction de masse) |
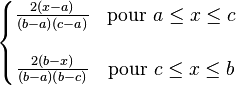
|
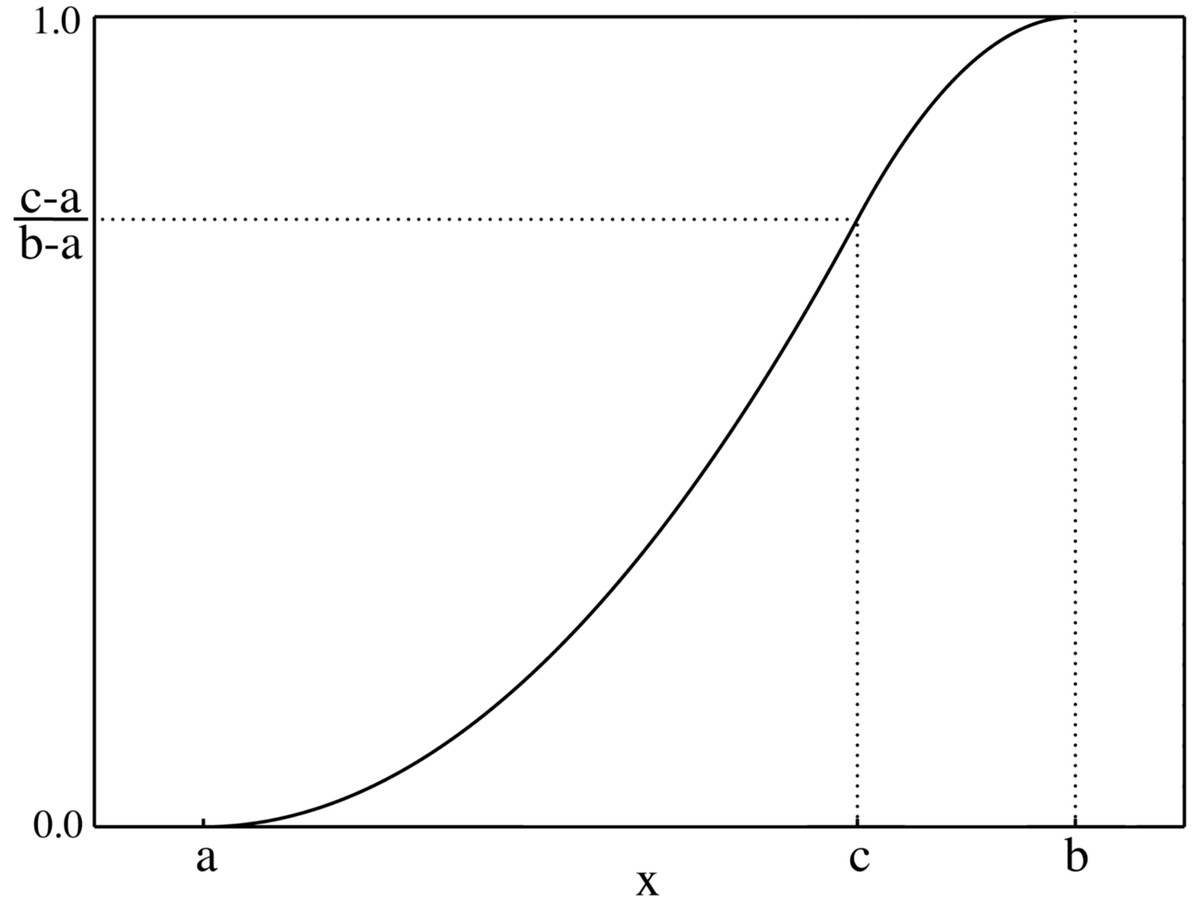
| Fonction de répartition |
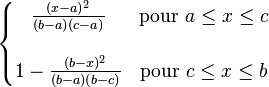
|
| Espérance |
|
| Médiane (centre) |
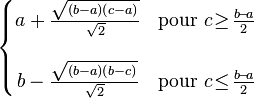
|
| Mode |
|
| Variance |
|
| Asymétrie (statistique) |
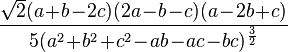
|
| Kurtosis (non-normalisé) |
|
| Entropie |
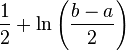
|
| Fonction génératrice des moments |
|
| Fonction caractéristique |
|
| modifier | |
Caractérisation
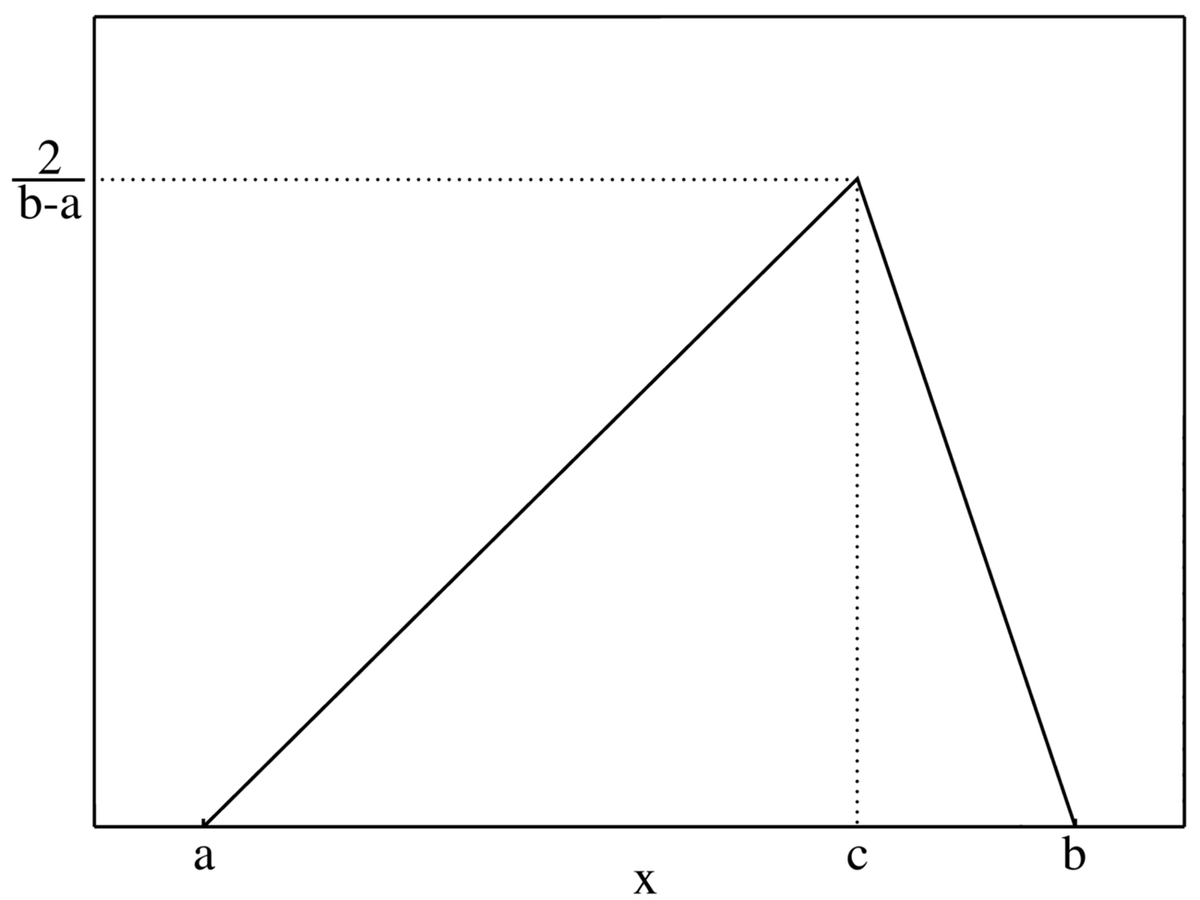
La loi triangulaire continue sur le support [a;b] et de mode c est définie par la densité suivante sur [a,b] :
Dans de nombreux domaines, la loi triangulaire est considérée comme une version simplifiée de la Loi bêta.
Liens avec la loi uniforme
Soit X1,X2 deux variables indépendamment et identiquement distribuées selon une loi uniforme standard. Alors:
- La distribution de la moyenne
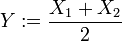
- La distribution de l'écart absolu Z: = | X1 − X2 | est aussi distribué selon une loi triangulaire de paramètres a=0, b=1 et c =0.