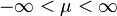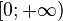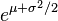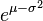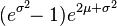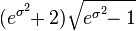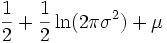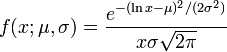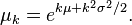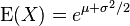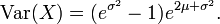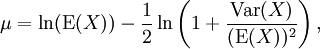Loi log-normale - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Loi Log-normale | |
|---|---|
| |
| |
| | |
| Paramètres | σ > 0 |
| Support |
|
| Densité de probabilité (fonction de masse) |
![\frac{1}{x\sigma\sqrt{2\pi}}\exp\left(-\frac{\left[\ln(x)-\mu\right]^2}{2\sigma^2}\right)](https://static.techno-science.net/illustration/Definitions/autres/d/df4bafde1c4e336639048b695e29e0cb_3df8fa0cc2fde5a7fee704068b002242.png)
|
| Fonction de répartition |
![\frac{1}{2}+\frac{1}{2} \mathrm{erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]](https://static.techno-science.net/illustration/Definitions/autres/2/253b03515b12e5affd383a2c2f022145_9c178f90ad801f1e1c16eeb9eb47b64c.png)
|
| Espérance |
|
| Médiane (centre) | eμ |
| Mode |
|
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) |
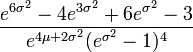
|
| Entropie |
|
| modifier | |
En probabilité et statistique, une variable aléatoire X est dite suivre une loi log-normale de paramètres μ et σ si la variable Y = ln(X) suit une loi normale de paramètres μ et σ.
Cette loi est parfois également appelée loi de Galton.
Une variable peut être modélisée par une loi log-normale si elle est le résultat de la multiplication d'un grand nombre de petits facteurs indépendants.
Caractérisation
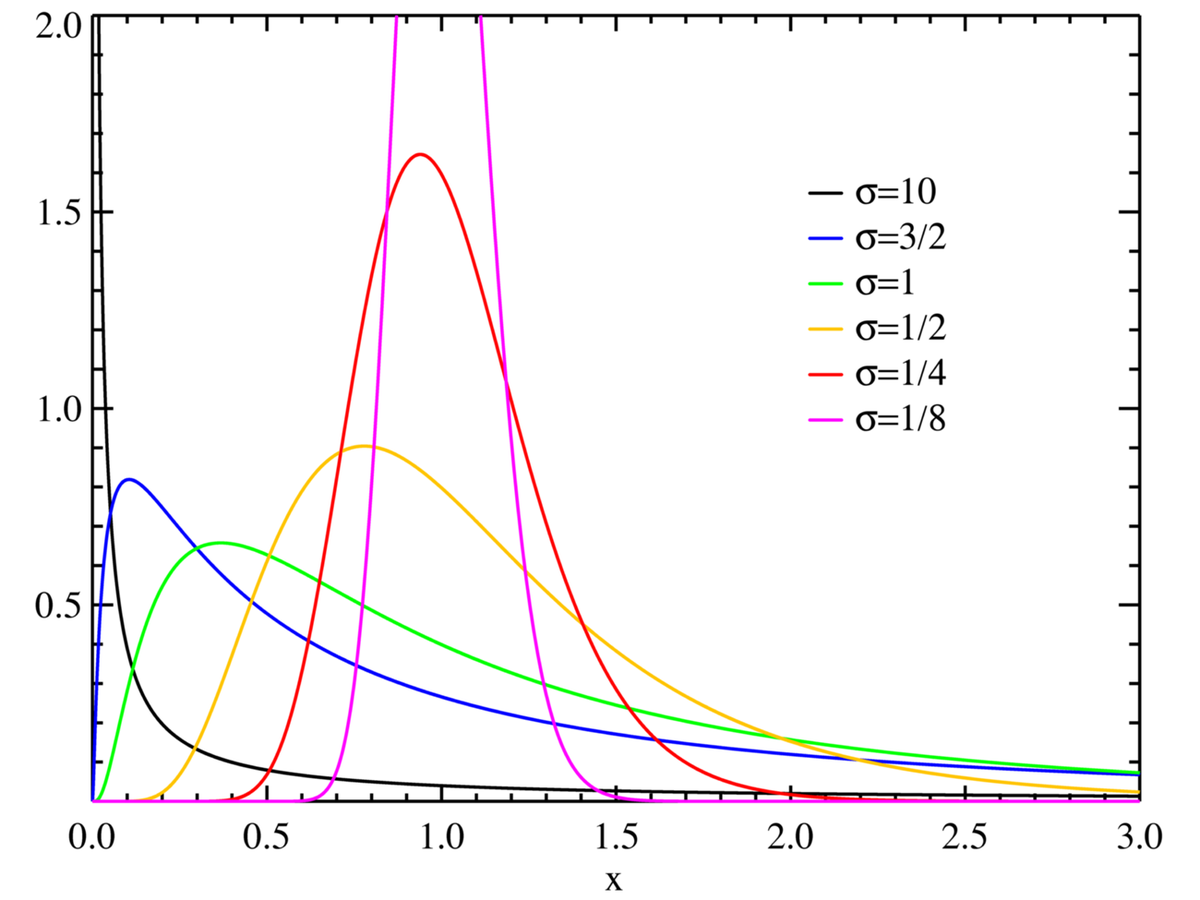
Densité
La loi log-normale de paramètres μ et σ admet pour densité
pour x > 0. μ et σ sont la moyenne et l'écart type du logarithme de la variable (puisque par définition, le logarithme de la variable est distribué selon une loi normale de moyenne μ et d'écart-type σ).
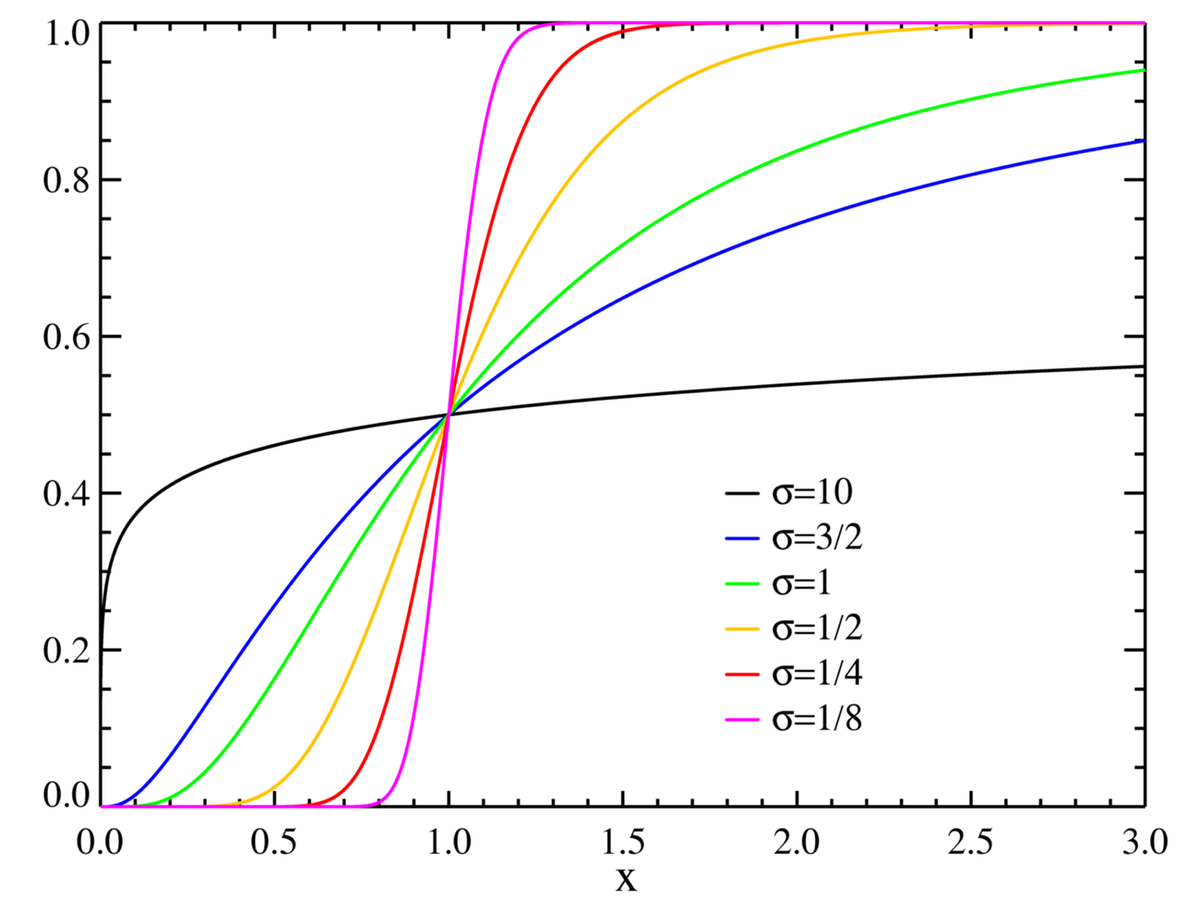
Fonction de répartition
Moments
Tous les moments existent et sont donnés par:
Espérance et écart-type
L'espérance est
et la variance est
Des relations équivalentes permettent d'obtenir μ et σ étant données l'espérance et l'écart-type:
Interprétation
Cette loi de distribution est particulièrement utilisée en analyse quantitative pour représenter les cours des instruments financiers (notamment actions, cours de change, taux d'intérêt, métaux précieux). Les cours ne peuvent pas être négatifs et il est plus pertinent d'exprimer les variations sous forme relative en pourcentage, donc les cours sont représentés généralement grossièrement par une loi log-normale.