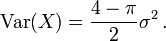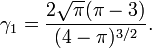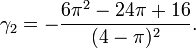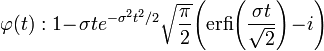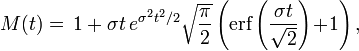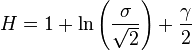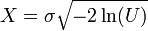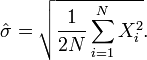Loi de Rayleigh - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Rayleigh | |
|---|---|
| |
| |
| | |
| Paramètres |  (nombre réel) (nombre réel) |
| Support |
|
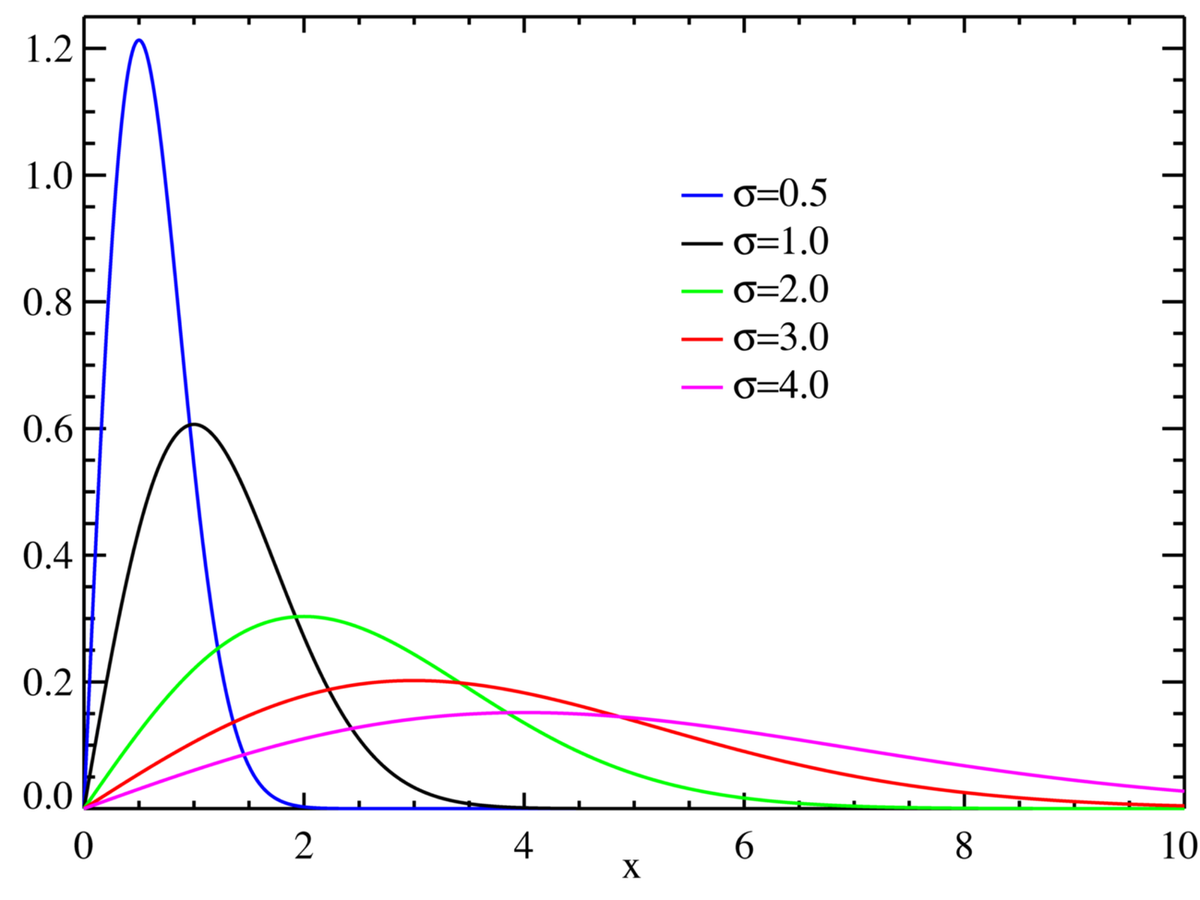
| Densité de probabilité (fonction de masse) |
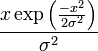
|
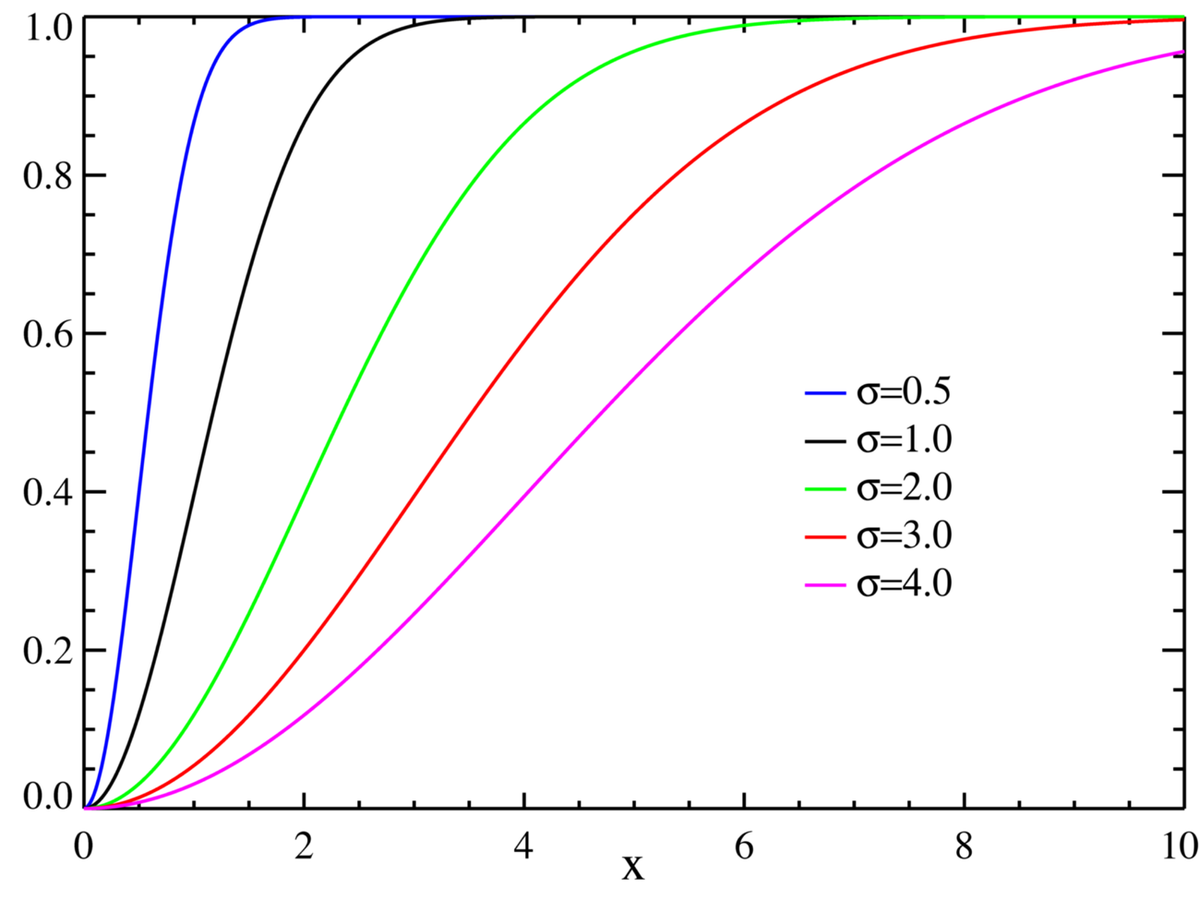
| Fonction de répartition |
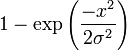
|
| Espérance |
|
| Médiane (centre) |
|
| Mode |
|
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) |
|
| Entropie |
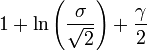
|
| Fonction génératrice des moments |
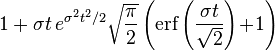
|
| Fonction caractéristique |
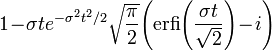
|
| modifier | |
En probabilités et en statistiques, la loi de Rayleigh est une loi de probabilité à densité. Elle apparaît comme la norme d'un vecteur gaussien bi-dimensionnel dont les coordonnées sont indépendantes, centrées et de même variance. Cette loi de probabilité est baptisée d'après Lord Rayleigh.
Typiquement, la distance
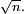
La densité de la loi de Rayleigh est
pour
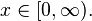
Propriétés
Les moments sont donnés par :
où Γ(z) est la fonction Gamma.
L'espérance et la variance d'une variable aléatoire de Rayleigh X sont les suivantes :
et
La skewness est :
La kurtosis est :
La fonction caractéristique est :
où
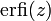
où
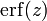
Entropie
L'entropie est
où γ est la constante d'Euler-Mascheroni.
Engendrer des variables de Rayleigh
Étant donnée une variable U uniforme sur l'intervalle (0, 1), la variable
suit la loi de Rayleigh de paramètre σ. Cela provient de la forme de la fonction de répartition, en particulier du théorème de la réciproque, et du fait que 1–U a même loi que U.
Estimation du paramètre
Étant données N variables de Rayleigh indépendantes et de même loi de paramètre σ, l'estimateur du maximum de vraisemblance de σ est
Lien avec certaines distributions discrètes
Marche aléatoire dans le plan
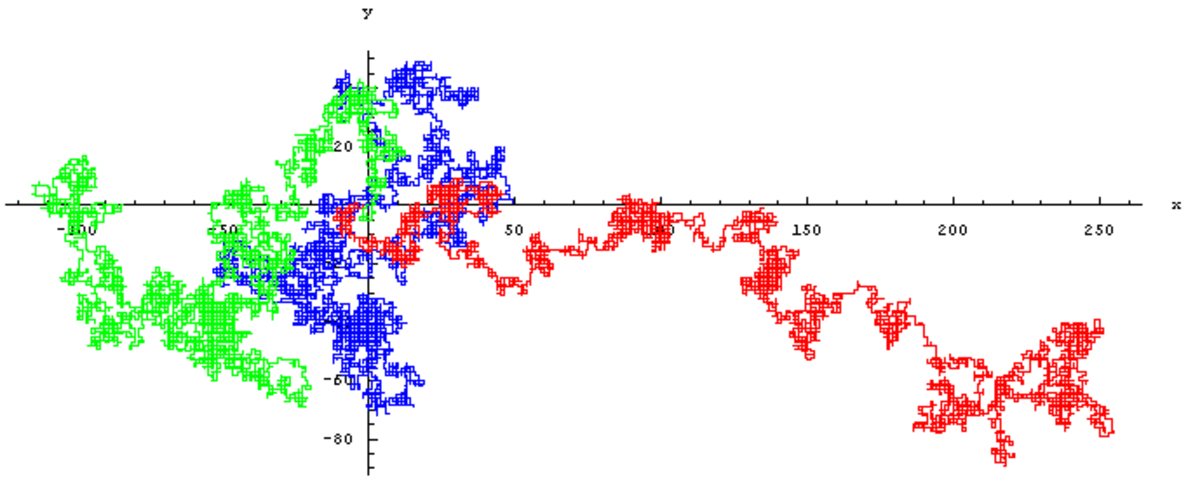
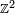
Notons
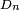
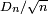
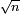
Distance entre deux points au hasard d'un arbre de Cayley aléatoire
À l'aide de la bijection de Joyal, on peut montrer que la loi de la distance
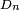
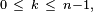
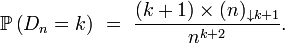
On peut montrer, par exemple à l'aide du lemme de Scheffé, que
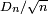
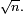
Points cycliques d'une application
En vertu de la bijection de Joyal, le nombre
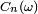

![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
![\scriptstyle\ [\![1,n]\!]](https://static.techno-science.net/illustration/Definitions/autres/4/4f7c2145ef89507b6795bb90369c150f_37b9a339e0652aec7caa1e9ca41d021e.png)
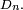
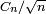
Problème des anniversaires
Cette loi discrète apparaît aussi dans des problèmes d'allocations (boules et urnes), dont le fameux problème des anniversaires. Lorsqu'on alloue séquentiellement des boules dans un ensemble de n urnes, avec équiprobabilité, ce qui revient à considérer un univers probabiliste
![\scriptstyle\ \Omega\ =\ [\![1,n]\!]^{\mathbb{N}},\](https://static.techno-science.net/illustration/Definitions/autres/3/38c42b67486631ccd41234f2921b5446_e4b84b4dc079c5f286b1a0dfe25ba1e9.png)
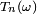
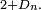
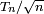
Pour n=365, soit 365 boîtes,
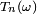
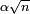
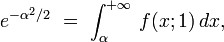
et vaut donc 1/2 pour un groupe d'approximativement
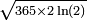
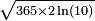
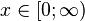
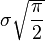
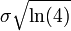
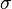
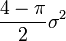
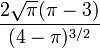
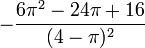
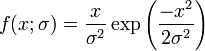
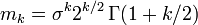
![\mathbb{E}[X] = \sigma \sqrt{\frac{\pi}{2}}\,](https://static.techno-science.net/illustration/Definitions/autres/9/9a1d889da48c8b9c5dec0ac2133a5ebf_84a9ee0300042c9f2470cb946aace599.png)