Ludolph van Ceulen - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Ludolph van Ceulen, ou Coelen, né à Hildesheim, le 28 janvier 1540, mort à Leyde le 31 décembre 1610, est un mathématicien allemand qui émigra aux Pays-Bas. Il fut le premier professeur de mathématiques rétribué par l'université de Leyde ; calculateur prodigieux, il obtint par les mêmes moyens qu'Archimède une valeur approchée de π avec 35 décimales exactes, record qui ne lui fut pas contesté pendant trente ans.
Biographie
D'Hildesheim à Anvers
Ludolph Van Ceulen est né en Allemagne, d'Hester de Roode (d'origine flamande) et de Johannes Van Ceulen, marchand peu fortuné, dans une famille nombreuse. Il ne fait pas d'étude universitaire et ne sait pas lire le latin ni le grec. Au début de sa vie, il gagne donc son pain comme professeur d'escrime, ce qui lui permet de rentrer en contact avec la bonne société de son époque.
D'après Meursius, Van Ceulen vit les années qui suivent la mort de son père en Livonie, puit rejoint son frère, Gert, à Anvers, où il prend ses premières leçons de mathématiques sous la férule de Johan Pouwelsz. Il y enseigne lui-même les mathématiques à partir de 1566.
Après un voyage en Allemagne en 1569, durant lequel il visite Cologne, Ceulen, dont le nom évoque cette ville, retourne sur Anvers. Membre de l'église calviniste des Pays-Bas, il est probable que Van Ceulen fut parmi les dizaines de milliers de protestants persécutés par le duc d'Albe aux environs de 1576 et qu'il partit avec un grand nombre d'entre eux vers Delft cette année-là.
La vie à Delft
Il épouse peu après sa première femme, Mariken Jansen, dont il a cinq enfants. On conserve sa trace à Delft par le certificat de baptême de sa fille Marie, née le 4 mai 1578 . Le 13 mai 1580, Ceulen demande au conseil de la ville de Delft l'autorisation d'ouvrir une école d'escrime et obtient le droit de s'installer dans l'église du monastère Saint Aghata, qui se trouve sans occupant. Une indemnité annuelle de 25 florins lui est allouée par la ville dans ce but.
De 1580 à 1584 quelques querelles mathématiques l'opposent à William Goudaan, (professeur de mathématiques d'Haarlem, qui réfute les travaux de Ceulen mais publie des solutions erronées à ses propres problèmes), et à Simon van der Eycke (à propos de la quadrature du cercle). Il publie en 1585 et 1586 des ouvrages dénonçant les erreurs de ses adversaires. Son amitié avec Adrien Romain date de cette année-là selon le R.P. Bosmans.
En 1587, le bourgmestre de Delft Jan Cornets de Groot, mathématicien amateur reconnu et père du juriste, Hugo Grotius, traduit pour lui les livres d'Archimède. Van Ceulen y peut lire qu'en découpant le cercle en 96 parties on montre que
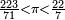
Il voyage à Brême en 1587 et en 1589 à Arnhem. En 1590, à la mort de sa première épouse, Van Ceulen se remarie (le 17 Juin) avec Adriana Simondochter, veuve la même année du professeur de mathématiques, et ami de Ceulen, Barthélemy Cloot. Elle a de son côté huit enfants.
L'université de Leyde
En 1594, il déménage avec toute sa famille à Leyde. Il y enseigne toujours les mathématiques et l'escrime. Le 9 juin 1594, le Conseil de Leiden l'autorise à ouvrir une école d'escrime à la Faliedenbegijnkerk
Après les élucubrations de l'humaniste protestant, Joseph Juste Scaliger, qui voulant se mêler de mathématiques, publie en 1594 une Cyclometrica elementa, où il déclare
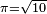
En 1595, il donne sa solution au problème qu'Adrien Romain posait aux mathématicien du monde entier, (mais particulièrement à Ceulen, le professeur de Wurzbourg tenant celui de Leyde pour le meilleur calculateur européen). Il en donne une solution de 24 décimales. La même année Viète donnera les 22 solutions positives de ce problème (une équation de degré 45) avec 8 décimales chacune.
En 1596, il publie néanmoins son propre livre, Van den circkel (« À propos du cercle »), ou il donne π avec 20 décimales, reléguant loin derrière Adrain Romain (15 décimales en 1595) et Viète (11 décimales en 1579). Pour cela, il utilise un polygone régulier de
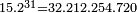
Le 13 mars 1598, il est nommé au comité chargé d'examiner les demandes de brevets pour les instruments maritimes en compagnie de Joseph Scaliger, Willebrord Snell et Simon Stevin. Il est de nouveau nommé à ce comité le 26 juin 1598}. En 1599 il siège au comité d'étude des impôts et des calculs des intérêts de la ville de Leyde, sous la présidence du même Joseph Scaliger.
En 1600 Le prince Maurice d'Orange ayant mis sur pied sa propre école d'ingénierie militaire, et l'ayant placée sous la direction de Simon Stevin, Van Ceulen y enseigne pendant les dix dernières années de sa vie l'arithmétique et l'arpentage en des cours d'une demi-heure, suivis d'une demi-heure de questions. Son élève le plus célèbre y est alors Willebrord Snell, qui traduit ses œuvres en latin.
En 1602, un de ses adjoints menace d'ouvrir sa propre école d'escrime, et Van Ceulen obtient du Conseil la fermeture de cette école concurrente. Lorsque il meurt en 1610, Van Ceulen, devenu professeur à l'université de Leyde, laisse dans son sillage 35 décimales de π.



















































