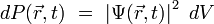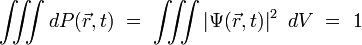Mécanique quantique - Définition
La liste des auteurs de cet article est disponible ici.
Formulation de la mécanique quantique par intégrale de chemin
Richard Feynman dans sa thèse en 1942 introduit la notion d'intégrale de chemin afin de présenter une nouvelle formulation de la mécanique quantique. Ces résultats ne seront publiés qu'en 1948 en raison de la seconde guerre mondiale. A terme, le but de cette approche serait de formuler une théorie de l'électrodynamique quantique en développant la quantification par intégrale de chemin. Si de nos jours on retient le formalisme Hamiltonien de la mécanique quantique pour traiter des problèmes classiques (au sens non relativiste), il s'avère que la formulation de Feynman est largement prédominante pour traiter les problèmes relativistes notamment en théorie quantique des champs, l'avantage c'est que cette approche est non perturbative.
Par ailleurs en 1953 Feynman appliqua son approche pour formuler la mécanique statistique quantique par intégrale de chemin (intégrale de Wiener, formule de Feynman-Kac) et tenta d'expliquer la transition lambda dans l'hélium superfluide.
Équation de Schrödinger
La formulation purement algébrique de Dirac peut paraître abstraite, mais elle eu le mérite de donner un cadre précis à la formulation alors en vogue à l'époque, en l'occurence la mécanique ondulatoire de Schrödinger.
La formulation de Schrödinger s'intéresse au mouvement d'une particule dans l'espace. La base de l'espace vectoriel des états y est donc naturellement l'ensemble
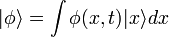
Où φ(x,t) est une fonction scalaire, que Schrödinger appelle fonction d'onde. Schrödinger fait du temps un simple paramètre, et non une grandeur physique, ce qui fait de sa théorie une théorie essentiellement non-relativiste.
En s'inspirant de l'équation de propagation électromagnétique, et à l'aide des relations de Planck et de de Broglie, Schrödinger parvient alors à exprimer l'évolution temporelle de φ(x) :
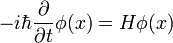
où H est un opérateur linéaire : l'hamiltonien du système considéré.
Interprétation physique de la fonction d'onde
L'interprétation physique de la fonction d'onde Ψ sera donnée par Born en 1926, et Dirac en fera plus tard son deuxième postulat, connu sous le nom de règle de Born : le module au carré de la fonction d'onde
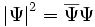
|
|
s'interprète comme étant la probabilité de trouver la particule dans un petit volume dV situé au voisinage du point
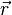
|
|
Cette interprétation statistique pose un problème lorsque le système quantique étudié est l'Univers entier, comme en cosmologie quantique. Dans ce cas, les physiciens théoriciens utilisent préférentiellement l'interprétation dite des « mondes multiples » d'Everett.
Méthodes de résolution
En dehors de quelques cas particuliers où on sait l'intégrer exactement, l'équation de Schrödinger ne se prête en général pas à une résolution analytique exacte. Il faut alors :
- soit développer des techniques d'approximations comme la théorie des perturbations.
- soit la résoudre numériquement. Cette résolution numérique permet notamment de visualiser la disposition curieuse des orbitales électroniques.