Mouvement de Lagrange de la toupie - Définition

Mouvement de Lagrange général

C'est évidemment plus compliqué si tous les OdG (Ordre de grandeur) se recoupent!

On peut montrer qu'il s'agit d'un mouvement à la Poinsot dans un référentiel bougeant à la Poinsot : il ne reste plus qu'à se représenter mentalement le mouvement.

Plus concrètement, le mouvement est intégrable, car il existe trois intégrales premières : puisque M = k/\K , L.k = constante = L1; L.K = constante = L2 et l'énergie E = 1/2L.ω + mga.cosθ.

Quelques calculs donnent une équation de Newton (voir diagramme horaire); donc le mouvement est intégrable à une quadrature près : E = 1/2 A , avec Ueff = mga.cosθ + L2²/2C + (L1-L2.cosθ)²/2(A.sin²θ).

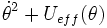
On doit distinguer en mathématiques 8 cas possibles. Mais pas en physique (voir pendule simple).

La discussion s'effectue essentiellement selon 2 grands cas possibles: pour theta = 0, Ueff(0) est infinie ou bien finie (ce qui exige la condition "impossible" en physique : L1 = L2); ensuite, dans le cas Ueff(0) finie, il reste à distinguer si exprimée en fonction de cos(theta), il y a minimum ou non. Les "bifurcations" et les séparatrices dans l'espace des phases ne sont vraiment sensibles qu'à l'œil exercé de qui veut bien regarder le détail de tout mouvement de cette toupie.

Œuf de Christophe Colomb : L²/4A > mga

Dans ce dernier cas, on trouve que si L1=L2 est suffisamment grand, la position verticale de la toupie est stable : L²/4A > mga est la condition dite de Colomb : la légende veut que Colomb prît un œuf (cuit) et le fît tenir vertical en le faisant tourner rapidement sur une table.

Si L1 différent de L2, il est facile de montrer que theta reste bloqué entre deux valeurs: les valeurs de théta inférieures à 90° sont dues , on s'en doute , à l'effet gyroscopique. Quand r(0) n'est plus suffisant, theta reste toujours bloqué entre deux valeurs (donc theta = 180° est impossible: c'est l'objet de multiples jeux de foire ; déquiller la quille du centre est impossible avec un pendule gyroscopique). Inversement un pendule gyroscopique lancé verticalement aura du mal à changer sa position verticale, et répondra moins que le simple pendule sphérique aux perturbations extérieures.

Précession uniforme

Comprendre que cette condition impose nutation nulle doit maintenant être assez intuitif. Et la vitesse de précession Pr est donnée par la formule :

L2.Pr - A. Pr². cosθ = mga

Ce qui peut se retrouver géométriquement :

Le vecteur K subit une précession sans nuter, (donc L est aussi en précession, sans nuter), autour de la verticale (on dit que la toupie ronfle; on dit qu'elle dort si theta est nul). Le moment dynamique est Pr k/\L = u [L2.Pr -A Pr².cos(theta)].sin(theta)et est égal à M = u mga.sin(theta) cqfd.

Les forts en mécanique pourront aussi appliquer le cours :

sachant que r = , on peut écrire directement :

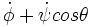
0 = couple gyro +couple de déséquilibrage dynamique + M , soit :

0 = -C .Pr.sinθ - (1/2).(C-A)Pr².sin2θ +mga.sinθ

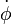
C'est bien le même résultat Ce résultat exact précise celui trouvé pour la balance gyroscopique.

Mouvement linéarisé

Reprendre les 3 équations exactes; et injecter les approximations suivantes :

• θ(t) = θ₀ + Y(t)
• ψ(t)sinθ₀ = t.Pr + X(t) , avec Pr = M/Cr(0)

et linéariser en (X,Y):

• X" + Pr².X + Y'. Couplage = 0
• -X'. Couplage + Y" = 0

avec Couplage = constante = (Cr(0)-2A.Pr.cosθ₀)/A, pratiquement égal à C/A r(0) en rad/s, caractérisant le couplage gyroscopique, qui conserve l'énergie : celle-ci ne peut que se tranférer de X vers Y et réciproquement.

La deuxième équation s'intègre immédiatement : -X . Couplage + Y' = constante = a

Soit X" + X(Pr² + Couplage²) + a.Couplage = 0

on trouve donc X(t) = cste + oscillation de pulsation = sqrt(Pr² + Couplage²) ~ Couplage = C/A r(0)

et Y(t) = b .t + oscillation de même pulsation .

On reconnaît le dessin d'une trochoïde plus ou moins allongée dessinée sur la sphère unité par le vecteur K : les pointes de la cycloïde sont toujours vers le haut (faire attention en projection horizontale selon que θ₀ > ou < π / 2).

• Application : m = 1kg; OG = a = 2cm ; A = m r² avec r = 4cm et C=mr'² avec r'= 3.6 cm (toupie-prolate); theta(0) = 30° ; r(0) = 4500 tours/minute donne :

theta-max -theta(0) = 3' ; nutation de période = 10 ms ; précession = 14°/s .