Mouvement de Lagrange de la toupie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le mouvement de Lagrange de la toupie est le mouvement d'une toupie pesante autour d'un point O de son axe, la réaction d'axe n'ayant pas de moment par rapport à O (rotule parfaite).
C'est à peu près le mouvement d'une toupie ordinaire, à ceci près que dans une toupie , le clou de la toupie est rond et glisse en frottant sur le plan où elle "repose" : il s'ensuit par application du théorème du couple gyroscopique qu'elle se redresse et vient en position de toupie dormante.
Le cas de Lagrange est mieux visualisé par le mouvement d'un gyroscope à deux axes de Cardan, surchargé : si la rotation est très rapide, la précession est directement proportionnelle au poids. On a donc une balance gyroscopique! Il convient d'étudier d'abord ce cas plus facile, avant d'aborder le cas général.
Balance gyroscopique : Précession = ~ mga/Cr(0)
- Description géométrique : on adopte les conventions suivantes pour les angles d'Euler: la rotation du premier cardan est définie par l'angle ψ(t) ; la rotation du deuxième cardan, intérieur au premier est la nutation
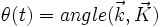
- Description cinématique : soit O, u l'axe des nœuds. le vecteur rotation est donc :
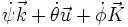
- Description cinétique : les inerties à la rotation propres sont A, A, C ;
l'énergie cinétique.2 est donc
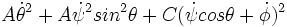
- Description dynamique :
le théorème du moment cinétique écrit selon u, K/\u, K donne les trois équations :
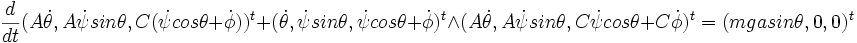
- Intégration dans l'approximation gyroscopique (vitesse de rotation propre très grande):
la troisième équation donne Lz = =cste = Cr(0) =~ C
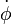
La deuxième équation donne θ = θ0 = cste : la nutation est constante.
La première équation donne
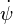
La précession « pèse » donc linéairement sur mga, indépendamment de la nutation.
On peut aussi considérer que cela n'est qu'artificiel, car le moment est en sinθ : alors , il est plus naturel de considérer le couple M et écrire
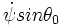
- Retrouver cela par le théorème du couple gyroscopique:
Cr(0)dK/dt = M= mga k/\K ; soit Cr(0).Pr.K/\k +mga k/\K = 0
Précession des équinoxes d'Hipparque
Cette fois, le moment M est celui du soleil sur le renflement équatorial. Soit Q le quadrupôle terrestre = 2(A-C)<0 : M = 3/4
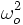
- Précession = -
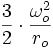
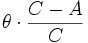
De la valeur de la précession (26 000 ans), on tire la valeur de (C-A)/C de la Terre.
En réalité, il faut aussi tenir compte de l'influence de la Lune : celle-ci intervient environ par le double (mais, inversement, la Lune subit le moment en retour, alors que le Soleil qui le subit aussi est influencé de façon négligeable suite à sa masse) : au 16"/an s'ajoutent donc 34"/an dus à la lune, soit 50"/an, soit un tour en 26 000 ans :
Hipparque ne savait pas mesurer le point Gamma avec la précision de 1" d'arc, mais il disposait des mesures antérieures vieilles de 2 siècles, soit 10 000" d'arc, ce qui suffisait.
Le pôle céleste n'est pas éternellement voisin de l'étoile polaire. En 26 000 ans, il décrit dans le ciel un cercle autour du point Q, de direction perpendiculaire à l'écliptique, point Q situé environ au milieu du Dragon (regarder sur un globe céleste le cercle écliptique (le Zodiaque suffit) et prendre la perpendiculaire à cet anneau) : le cercle de 23°26' est très large et emmènera dans 13 000 ans le pôle vers la constellation du Cygne (à vérifier!) : alors du point de vue climat, l'hémisphère nord recevra cette fois un peu plus de chaleur que l'hémisphère sud (~ 7%), ce qui est important dans la théorie de Milancovitch du climat (il faut y rajouter la variation périodique d'excentricité e(t) et la variation périodique d'inclinaison i(t) (stabilisée par l'existence de la Lune!) On obtient ainsi une remarquable concordance avec les cycles glaciaires de l'holocène.
A noter que le plan orbital de la Lune est décalé par rapport à l'équateur terrestre et l'écliptique; il en résulte un léger décalage de 9" d'arc et une période d'1 saros ( 18.6 ans); cet effet est négligeable sur le climat , certes!

















































