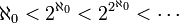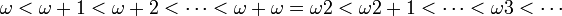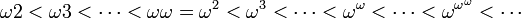Nombre transfini - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les nombres transfinis sont des nombres infinis découverts et explorés par le mathématicien Georg Cantor. Se basant sur ses résultats, il a introduit une sorte de hiérarchie dans l'infini, en développant la théorie des ensembles. Un nombre entier naturel peut être utilisé pour décrire la taille d'un ensemble fini, ou pour désigner la position d'un élément dans une suite. Ces deux utilisations correspondent aux notions de cardinal et d'ordinal respectivement. Bien que semblables en apparence, ces deux concepts cantoriens doivent être distingués lorsque l'on s'intéresse à des ensembles infinis.
Aspect épistémologique
Les travaux de Cantor sur la théorie des ensembles ont été à la source de nombreux paradoxes, et ont contribué à la crise des fondements qu'ont connue les mathématiques, entre la fin du XIXe et le début du XXe siècle. Kronecker, par exemple, a exprimé pourquoi il ne considérait pas comme mathématiquement valides les démonstrations de Cantor faisant intervenir l'infini de deux façons différentes, en considérant l'un comme achevé et l'autre comme en construction.
Une fameuse boutade de David Hilbert résume le choix de bon nombre de mathématiciens : « Cantor a créé pour les mathématiciens un paradis dont ils ne se laisseront pas expulser ».
Les nombres transfinis ont peu d'applications en dehors des mathématiques à l'heure actuelle.
Nombres cardinaux transfinis
Dans la théorie des ensembles de Zermelo-Fraenkel avec axiome du choix, à tout ensemble correspond un cardinal, à savoir le plus petit nombre ordinal en bijection avec cet ensemble. Le cardinal d'un ensemble fini à n éléments est n. Le cardinal ω de l'ensemble infini

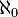
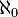
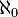
- l'union de

- l'union d'une suite finie d'ensembles infinis dénombrables
- le produit d'une suite finie d'ensembles infinis dénombrables
Ces propriétés se traduisent sur le nombre transfini
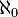
-
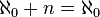
-
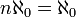
-
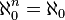
Mais l'infini ne se résume pas à
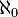

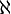

-
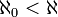
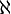
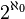


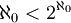
Il existe donc une infinité de nombres cardinaux transfinis !
Se pose alors la question de savoir si
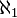
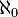
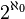
Nombres ordinaux transfinis
En théorie des ensembles, les entiers naturels peuvent être construits avec des ensembles :
- 0 = {} (ensemble vide)
- 1 = {0} = { {} }
- 2 = {0,1} = { {}, { {} } }
- 3 = {0,1,2} = {{}, { {} }, { {}, { {} } }}
- 4 = {0,1,2,3} = { {}, { {} }, { {}, { {} } }, {{}, { {} }, { {}, { {} } }} }
- etc.
De cette manière, tout entier naturel est un ensemble bien ordonné, et l'inclusion des ensembles se traduit par un ordre sur les entiers naturels. Cela nous conduit à la définition d'un nombre ordinal par John von Neumann : un ensemble E est un ordinal si et seulement si E est totalement ordonné pour l'inclusion et tout élément de E est un sous ensemble de E. Cette approche permet d'envisager les nombres ordinaux infinis, appelé aussi nombres ordinaux transfinis.
L'existence des ordinaux infinis est assurée par l'axiome de l'infini.
Le premier nombre ordinal transfini est noté ω, dernière lettre de l'alphabet grec. Il correspond à l'ensemble des nombres entiers naturels
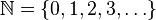
Si α et β sont deux ordinaux, on dit que α < β si et seulement si
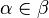
Si α est un ordinal, on définit le successeur de α comme étant l'ordinal
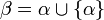
Cette addition est associative mais pas commutative. Ainsi ω < ω + 1 < ω2, mais ω = 1 + ω. On peut aussi définir une multiplication et une exponentielle, ce qui donne lieu à une arithmétique sur les nombres ordinaux transfinis.
Il existe des nombres ordinaux transfinis qui ne peuvent pas être obtenus en effectuant un nombre fini d'opérations arithmétiques n'utilisant que les nombres ordinaux finis et ω. Le plus petit d'entre eux est appelé ε0 et vaut
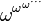
Les ordinaux ne forment pas un ensemble, au sens des axiomes de la théorie des ensembles, mais une classe propre. Cette propriété s'appelle le paradoxe de Burali-Forti, sa démonstration repose sur l'argument suivant: si l'ensemble des ordinaux existait, il serait par définition un ordinal qui serait strictement plus grand (par définition) que tous les ordinaux, ce qui est contradictoire.