Nombre hypercomplexe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le terme nombre hypercomplexe est utilisé pour désigner les éléments des algèbres qui sont étendues ou qui vont plus loin que l'arithmétique des nombres complexes. Les nombres hypercomplexes ont eu un grand nombre de partisans incluant Hermann Hankel, Georg Frobenius, Eduard Study et Elie Cartan. L'étude des systèmes hypercomplexes particuliers conduit à leur représentation avec l'algèbre linéaire. Cet article donne une vue d'ensemble des différents systèmes, incluant certains types qui n'ont pas été considérés par les pionniers avant la perception moderne issue de l'algèbre linéaire. Pour les détails, les références et les sources, suivre le lien associé au nombre particulier.
Des nombres avec une dimensionnalité
L’usage le plus commun du terme nombre hypercomplexe fait référence sans doute aux systèmes algébriques avec une dimensionnalité (axes), comme ceux contenus dans la liste suivante. Pour les autres (comme les nombres transfinis, les nombres superréels, les nombres hyperréels, les nombres surréels), voir sous l'entrée nombre.
Malgré leurs différentes propriétés algébriques, aucune algèbre hypercomplexe n’a de structure de corps algébrique, car elle formerait alors une extension algébrique du corps des complexes


Nombres distributifs avec un axe réel et n axes non-réels
Une définition accessible et moderne d'un nombre hypercomplexe est donnée par Kantor et Solodovnikov (voir la référence complète ci-dessous). Ils sont éléments de systèmes de nombres unitaires et distributifs qui contiennent au moins un axe non-réel et sont clos pour l’addition et pour la multiplication. Les axes sont générés par les coefficients réels
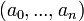
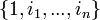
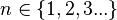
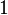
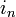
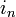
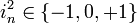
D’un point de vue géometrique, ces nombres forment des algèbres sur les nombres réels de dimension finie.
Les classifications suivantes obéissent à cette catégorie.
Quaternion, octonion et au-delà : la construction de Cayley-Dickson
Les nombres hypercomplexes sont obtenus en généralisant plus avant la construction des nombres complexes à partir des nombres réels par la construction de Cayley-Dickson.
Celle-ci permet d’étendre les nombres complexes en systèmes de nombres de dimensionnalité
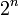
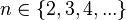
Augmenter la dimensionnalité introduit des complications algébriques : la multiplication des quaternions n’est plus commutative, la multiplication des octonions est, de plus, non-associative et les sédénions sont non-normés.
Dans la définition de Kantor et Solodovnikov, ces nombres correspondent aux bases anti-commutatives de type
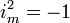
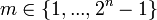
Puisque les quaternions et les octonions offrent une norme (multiplicative) similaire aux longueurs des espaces vectoriels euclidiens de dimensions quatre et huit respectivement, ils peuvent être associés à des points dans certains espaces euclidiens de dimensions plus élevées. Au-delà des octonions, par contre, cette analogie tombe puisque ces constructions ne sont plus normées.
On peut créer une infinité d’algèbres du même type en appliquant la construction de Cayley-Dickson à l’algèbre de rang inférieur. Quelques propriétés intéressantes sont à noter :
- À chaque rang, les dimensions des nombres sont doublées ;
- À chaque rang, une propriété supplémentaire est perdue.
| n | 2n | nom | limite |
|---|---|---|---|
| 0 | 1 | réels | - |
| 1 | 2 | complexes | perte de la comparaison |
| 2 | 4 | quaternions | perte de la commutativité |
| 3 | 8 | octonions | perte de l'associativité |
| 4 | 16 | sédénions | perte de l'alternativité |
Après les octonions, les algèbres contiennent des diviseurs de zéro (x · y = 0 n'implique plus x = 0 ou y = 0), ce qui implique que leurs multiplications ne conservent plus les normes.
Nombre dual
Les nombres duaux sont de bases
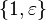
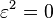
Algèbre complexe fendue
Les nombres complexes fendus sont de bases
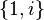
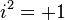
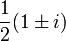
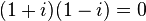
Une construction de Cayley-Dickson modifiée conduit aux coquaternions (quaternions fendus, c’est-à-dire de bases
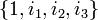
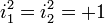
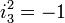
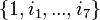
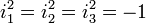
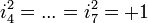
Toutes les bases non-réelles d'algèbres complexes fendues sont anti-commutatives.
Algèbre de Clifford
Une algèbre de Clifford est une algèbre unitaire, associative sur les espaces vectoriels réels, complexes ou quaternionique muni d'une forme quadratique. Alors que les constructions de Cayley-Dickson et complexes fendues avec huit ou plus de dimensions ne sont plus associatives en respectant la multiplication, les algèbres de Clifford conservent l’associativité pour toute dimensionnalité.
Tessarine, biquaternion et sédénion conique
Tandis que pour les constructions de Cayley-Dickson, l’algèbre complexe fendue et l’algèbre de Clifford, toutes de bases non-réelles sont anti-commutative, l’utilisation d’une base imaginaire commutative conduit aux tessarines à quatre dimensions et aux biquaternions à huit dimensions.
Les tessarines offrent une multiplication commutative et associative, les biquaternions sont associatifs mais non commutatifs et les sédénions coniques sont non-associatifs et non-commutatifs. Ils contiennent tous des éléments idempotents et des diviseurs de zéro, sont tous non-normés, mais offrent un module multiplicatif. Les biquaternions contiennent des éléments nilpotents.
Compte tenu de l’exception de leurs éléments idempotents, des diviseurs de zéro et des éléments nilpotents, l’arithmétique de ces nombres est close pour la multiplication, pour la division, pour l’exponentiation et pour les logarithmes (voir les quaternions coniques, qui sont isomorphes aux tessarines).
Quaternion hyperbolique de A. MacFarlane
Les quaternions hyperboliques d’Alexander MacFarlane ont une multiplication non-associative et non-commutative. Néanmoins, ils offrent une structure d’anneau plus riche que l’espace de Minkowski de la relativité restreinte. Toutes les bases sont des racines de 1, c’est-à-dire
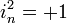
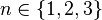
Nombre multicomplexe
Les nombres multicomplexes sont une algèbre à n dimensions commutative générée par un élément