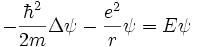Orbitale de l'atome d'hydrogène - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
On appelle orbitales de l' atome d'hydrogène, les solutions stationnaires de l'équation de Schrodinger de l'atome d'hydrogène. (voir Théorie de Schrödinger de l'atome d'hydrogène). À chaque état stationnaire correspond une énergie En ; mais à chaque niveau d'énergie, il y a n² orbitales, soit 2n² spin-orbitales. L'orbitale (1s) a été amplement discutée dans l'article atome d'hydrogène.
États stationnaires des couches L, M
Les autres valeurs propres et les autres états propres sont plus difficiles à calculer. On se contentera ici de leur description. Pour la démonstration, voir Théorie de Schrodinger de l'atome d'hydrogène.
Niveaux d'énergie
Le spectre de l'hydrogène est connu avec une précision exceptionnelle ; il en est de même pour l'ion He+, et l'ion Li++, etc. que l'on forme assez facilement par spalliation. Mais il faudra tenir compte de la variation de la masse réduite (cf. atome de Bohr, hydrogène de Pickering ) ; et bien sûr du changement de e² en Ze², Z étant la charge du noyau. Le tracé expérimental de -E(Z,n).n²/Z², corrigé de la masse réduite et de légers effets relativistes (qui varient comme Z²) est assez fascinant de platitude, alors qu'on peut aller jusqu'à des n de l'ordre de 80 , et Z de l'ordre de 15.
- D'autre part, pour l'atome ou ion à N électrons, on pourra comparer les niveaux d'énergie E(N,Z,n,l,m)/Z² pour le même N : ils sont assez analogues bien que le problème soit très différent (cf. atome à N électrons).
- Enfin signalons le cas des atomes hydrogénoïdes (les alcalins ou ions qui y correspondent : le dernier électron, surtout s'il est excité, présente un spectre très analogue à celui de l'hydrogène, car les électrons des couches inférieures de symétrie sphèrique, du fait du théorème de Gauss, écrantent la charge Z du noyau, ne laissant apparaître, surtout pour les orbitales de l= n-1, m=0 , qu'une charge écrantée Z(effectif)= Z-(N-1) apparemment ponctuelle.
- Rappel : pour des Z élevés, les électrons dits de couche profonde de l'atome à N électrons, par exemple les électrons 1s , seront à des énergies très basses ( -Z².13.6 eV , soit pour Z =10 , des énergies déjà 100 fois 13.6 eV ): sachant que la chimie ne porte que sur des énergie au plus de qq dizaines d'eV , il apparaît déjà clair que ces électrons ne joueront aucun rôle en chimie. Seuls les électrons de valence interviendront ; et c'est bien là l'essentiel de ce que dit la classification périodique.
Allure des orbitales
Il est extrèmement important de se représenter les orbitales
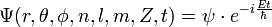
Ne pas oublier aussi que [même pour les états (ns)] , l'énergie cinétique de l'électronde-délocalisé est la moitié de l'énergie électrostatique : il convient de se représenter mentalement le couple [densité électronique , phase électronique], couple qui sera si important en chimie quantique pour apparier les électrons : dans l'équation de Schrodinger sur le corps des complexes , on ne répètera jamais assez qu'il y a DEUX équations réelles couplées : l'une considère le module de psi,soit a, l'autre la phase,soit S/

|
on aura :
|
et
|
- La première équation s'appelle la conservation de la densité électronique avec un courant de probabilité .
- La deuxième équation s'appelle équation de l'eikonale de Schrodinger.
Et donc tout cela "bouge" de façon stationnaire, via des tirages au sort de probabilités stationnaires.
- Les calculs (assez ardus ?) montrent que les fonctions d'onde s'expriment en coordonnées polaires sous la forme :
|
- n est le nombre quantique principal
- l est le nombre quantique azimutal
- m est le nombre quantique magnétique
- k: = n − l + 1 est le nombre de zéros de la fonction
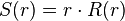
les fonctions
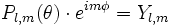
Dans ce cas, chaque fonction d'onde individuellement donnera une vision simplifiée : le courant
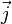
D'autre part, il n'y a pas de "gelée électronique" représentant peu ou prou l'électronde délocalisé, même s'il est éminemment utile de tracer les orbitales chimiques.
Enfin, l'équation de l'eikonale se réduit simplement à ce qu'on appelle l'équation de Schrodinger stationnaire:
|
Lors de l'hybridation des orbitales, il conviendra de reprendre ces calculs : la linéarité sur le corps des complexes produit des termes d'interférence constructive et destructive, si caractéristiques de la chimie quantique.[une orbitale hybridée est superbement représentée dans l'article atome ]. .
Réprésentation des harmoniques sphériques
- La représentation des harmonique sphérique est excellemment faite dans ce lien.
On pourrait essayer une réprésentation(cf. White 1935), si possible de façon dynamique !
- Une fois bien saisie la forme des Ylm et leur symétrie, la deuxième chose dont on doit se souvenir est que en gros la théorie de Bohr est satisfaite via les R(r).
variance de la position
On peut rappeler plus précisément :
moyenne de 1/r = Z/n², indépendante de l , c'est la dégénérescence "accidentelle" déjà vue.
variance(1/r) = Z²/n⁴ [
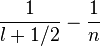
Donc la variance relative est grande pour les états s , mais pour les états de Rydberg décroît comme ~ 1/2n² , soit pour n = 60, inférieure à 2.10^(-4) et les Y(n-1 , m) donnent pour une "bonne combinaison", une bonne localisation en théta = 90° et en phi(t) : en gros, le paquet d'ondes qui représente l'électronde-délocalisée n'est pas si délocalisé que cela, et on retrouve assez bien l'image classique de Bohr; mais cela ne dure pas: le paquet d'ondes s'étale.
Cela dit :
moyenne de r : 1/2Z . [3n²-l(l+1) ] : un électron s ( l=0) est beaucoup plus "loin" et plus "proche" du noyau qu'un électron de Rydberg (l = n-1).Cela n' a rien de paradoxal si l'on pense à une comète, et en mécanique quantique à la délocalisation de l'électectronde.D'ailleurs,
moyenne de r² : 1/2Z² . n²[5n²+1-3l(l+1)]
On voit donc que la variance d'un électron s est n⁴/4 , la variance relative est 1/9 ~11% : c'est énorme, compte-tenu de la taille de r(n) = n².r(1) : Si l'on imagine cela pour toutes les planètes, il y aurait un gros grabuge dans le système solaire. Dans l'atome, il faut bien s'imaginer que si n= 3 ou n= 4 , un électron s pénètre beaucoup dans les couches profondes (il correspondrait à une comète en mécanique céleste), et va donc interagir avec celles-ci : cette question devra être examinée soigneusement dans le cas de l'atome à N électrons.
Au contraire, pour un électronde de Rydberg :
variance(r) = 1/4Z² .[n²(n+2) - l²(l+1)²] soit avec l= n-1: [2n³+n] donc une variance relative en ~ 1/2n.
- Remarque : la valeur moyenne de 1/r³ se trouve astucieusement reliée à celle de 1/r² : Z/r² - l(l+1)/r³ =0 , en moyenne.
- Remarque : les relations de Pasternak donnent toutes les valeurs moyennes de r^p , p entier.
Couche L
elle comprend une orbitale (2s) sphérique et 3 orbitales (2p) en "larmes d'eau": voir harmonique sphérique
- orbitales 2p : k=15
figure ici
- orbitales 2s : k=12
à symétrie sphérique figure ici
Couche M
elle comprend une orbitale (3s) sphérique, et 3 orbitales (3p) en larmes d'eau scindées une fois, et 5 orbitales (3d), l'une à symétrie de révolution la 3d(z²-3r²), et 4 en trèfle à 4 lobes : 3d(xy),3d(yz), 3d(zx) et 3d(x²-y²). Voir harmonique sphérique.
- orbitale 3d de révolution :k=1230
figure ici
- orbitale 3d(xy):k=1010
figure ici
les 3 autres orbitales s'en déduisent par symétrie.
- orbitale 3p :k=1
en larmes d'eau scindées une fois
figure ici
- orbitale 3s , sphérique, scindées deux fois: k=2
figure ici.
Tout cela est aussi valable pour les espèces iso-électroniques, comme l'ion borique B3+, à condition de changer e^2 en Z.e^4.
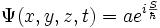
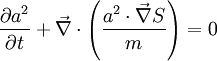
![{\partial S \over \partial t} + {1 \over 2m}(\vec\nabla S)^2 +\left[V(x,y,z) - \frac{\hbar^2}{2m}{\Delta a \over a }\right] = 0](https://static.techno-science.net/illustration/Definitions/autres/5/5a47be8f960b7f44e3132b3ea48d8fbb_b7b87ebd69c7870360c8f0c3d8f3fc69.png)
![\Psi_{n,l,m}(r,\theta,\phi,t) = R_{n,l}(r)\cdot P_{l,m}(\theta)\cdot e^{i[m\phi -{E_n t \over \hbar}]}](https://static.techno-science.net/illustration/Definitions/autres/4/41678cfa5a1b675d7823d6d57d420470_bd7919e90deababdfaf6f946b6526078.png)