Paradoxe des jumeaux et l'effet Sagnac - Définition

Introduction

Le paradoxe des jumeaux et l'effet Sagnac est une étude du paradoxe des jumeaux de Langevin dans le cadre des repères en rotation et faisant intervenir l'effet Sagnac.

Ici, Bernard, au lieu de faire demi-tour pendant son voyage effectue un parcours circulaire le faisant revenir à son point de départ. Bien qu'il n'effectue pas de demi-tour brutal, il subit toutefois une accélération centripète et la situation est analogue au paradoxe des jumeaux classiques. Toutefois, faire intervenir un repère en rotation permet une variété de situations très intéressantes.

L'analyse correcte de ces situations nécessite une analyse approfondie de l'effet Sagnac.

Le repère inertiel sera noté R. Passons en revue quelques situations.

Deux jumeaux, un immobile, l'autre en rotation

Le premier cas est celui où Alain est immobile dans le repère inertiel R et regarde Bernard tourner autour de lui.

En fait, l'effet Sagnac n'intervient guère ici et on se retrouve dans une situation classique où l'un des jumeaux est inertiel et l'autre accéléré.

La trajectoire d'Alain et Bernard dans le repère R s'obtient aisément.

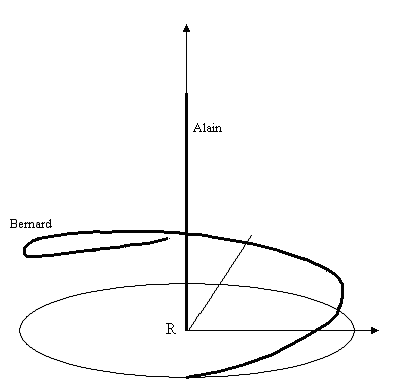
Ensuite on effectue l'intégrale du temps propre comme expliqué dans le paradoxe des jumeaux.

Ici, c'est particulièrement simple car la trajectoire est tangente en tout point à des droites de pente constante. C’est-à-dire que la vitesse de Bernard, en grandeur, est constante (si la rotation est uniforme). On peut donc utiliser la classique dilatation du temps.

Que se passe-t-il si par exemple Alain est au bord du disque (dans la figure ci-dessus, il est au centre) ? Quel est le vieillissement de chacun après un tour de Bernard ?

Ainsi, pour un cercle de rayon R et une vitesse angulaire ω, le temps pris par Bernard (dans le repère R) pour faire un tour est de :

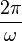
C'est le vieillissement d'Alain.

Le facteur relativiste gamma Γ correspond à la vitesse tangentielle Rω. Et le vieillissement, plus faible, de Bernard est donc :

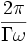
C'est, sommes toutes, un paradoxe des jumeaux tout à fait classique !

Deux jumeaux font un tour dans chaque sens sur un disque en rotation

Considérons maintenant deux jumeaux placés sur un disque ayant une rotation ω₀. Chacun part faire un tour d'un côté à une vitesse angulaire ω par rapport au disque.

Ainsi, Alain tourne (dans R) à la vitesse angulaire ω + ω₀ et Bernard à ω₀ − ω. On suppose par facilité que ω est plus grand que ω₀ mais ce n'est pas une nécessité. Donc ω₀ − ω est négatif et Bernard tourne dans l'autre sens. R' est ici le repère attaché au disque en rotation.

La présence du disque est totalement superflue, nous ne l'utilisons que par facilité de raisonnement. L'important est le fait que Alain et Bernard aient des vitesses angulaires différentes dans le repère inertiel R. Par exemple ω₁ et ω₂ (ω₁ et ω₂ sont supposés positifs et ω₁ > ω₂, le signe moins indiquant qu'il tourne dans l'autre sens).

Cela correspond à une vitesse angulaire du "disque" (réel ou fictif) . Le repère R' sera un repère attaché au disque ou, si celui-ci n'existe pas, un simple repère en rotation dans R à la vitesse angulaire donnée par cette relation.

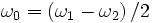
Considérons le point de vue du repère R. La situation est clairement non symétrique.

Le graphe est analogue au précédent mais chacun parcourt une spirale dans l'espace-temps avec un angle différent (le pas de la spirale est différent). Le croisement après un tour ne se produit d'ailleurs pas au même point de R que le point de départ. Chacun subit une dilatation du temps (du point de vue de R) et donc l'âge des jumeaux sera différent à leur rencontre.

Quel est le point de vue dans R' ? Cette fois la situation semble symétrique puisque les deux jumeaux partent faire un tour à des vitesses angulaires identiques dans chaque sens.

Mais R' n'est pas inertiel. L'espace n'y est pas plat. Et nous tombons sur l'effet Sagnac.

Après un tour complet dans chaque sens l'âge des jumeaux sera différent de deux fois le Time Gap (l'étude de l'effet Sagnac a montré qu'il est universel, le même quelle que soit la vitesse des "objets", ici les jumeaux, qui font le tour).

Le calcul détaillé montre évidemment que la différence d'âge est identique selon les deux points de vue.