Paradoxe des jumeaux et l'effet Sagnac - Définition

Les deux jumeaux font un tour dans chaque sens

Regardons maintenant la situation où chaque jumeau fait un tour dans R, à même vitesse angulaire, mais chacun dans un sens.

Les trajectoires sont les mêmes que ci-dessus mais chaque jumeau tourne dans un sens différent.

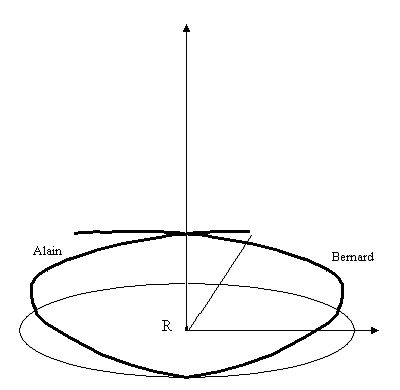
La situation est totalement symétrique et à leur deuxième rencontre (après un demi-tour) ou troisième (après un tour) ils auront le même âge.

Pour un observateur dans R, chaque jumeau a vieilli de

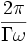
après un tour et il est donc normal que les jumeaux aient le même âge.

Nous avons là à nouveau une situation assez classique de jumeaux totalement symétriques.

Tourner autour d'une planète

Certaines variantes du paradoxe des jumeaux invoquent l'utilisation d'une planète.

Un des jumeaux est loin dans l'espace tandis que l'autre poursuit une trajectoire l'amenant près de la planète. Il utilise cette planète pour faire demi-tour et revient près de son frère.

L'argument principal est que les deux frères sont dans des repères inertiels et donc que l'on retombe sur le paradoxe des jumeaux.

Pourquoi ces repères sont-ils inertiels ? Nous touchons là à tout ce qui concerne la gravitation. La gravitation obéit au principe d'équivalence (qui est en fait un postulat). Tous les corps sont accélérés dans un champ de gravitation de la même manière, quels que soient leurs masses, leurs volumes, leur composition,... Le premier à avoir montré cela est Galilée avec sa célèbre expérience à la tour de Pise où il a laissé tomber du haut un boulet plein et un boulet creux et vérifié qu'ils arrivaient en même temps au sol. Grâce à ce principe, Einstein a montré qu'un repère en chute libre était équivalent à un repère inertiel. Si vous avez la chance (ou la malchance) de vous trouver un jour dans un ascenseur qui s'est décroché, faites l'expérience, lâchez un stylo : il va flotter près de vous. Tout simplement parce qu'il tombe à la même vitesse que vous. Vous avez certainement déjà vu aussi à la télévision ce type de situation réalisée lors de vols balistiques avec un avion adapté et qui sert à l'entraînement des astronautes. Un tel ascenseur en chute libre est donc physiquement identique à une cabine en apesanteur, loin dans l'espace et totalement libre (sans aucune force appliquée ni accélération). Un repère en chute libre est donc inertiel !

C'est ce principe d'équivalence qui permet une description géométrique de la gravitation ! Puisque la gravitation dépend de l'environnement et du lieu où on se trouve et pas du corps placé à cet endroit, alors on peut décrire géométriquement son mouvement dû à la gravitation. Dans ce cadre, la gravitation n'est plus considérée comme une force au même titre que les autres et un corps soumis à la seule gravitation (donc en chute libre) est inertiel.

Entre parenthèse, la relativité générale montre que la gravitation nécessite forcément une description à l'aide d'un espace-temps courbe. Le repère inertiel en chute libre est décrit par un espace-temps de Minkowski qui n'est autre qu'un espace tangent à l'espace courbe complet. Comme la courbure de l'espace-temps est donnée par la matière (à travers l'équation d'Einstein), voilà la justification de l'existence des repères inertiels.

Fermons la parenthèse gravitationnelle nécessaire pour comprendre le contexte et revenons à l'affirmation que les jumeaux passant près des planètes constituent un véritable paradoxe des jumeaux.

On peut invoquer deux argumens contre cela :

1. Si l'un des jumeaux utilise la planète pour faire demi-tour, alors il est soumis à un champ gravitationnel différent de son frère et les effets de la gravité prédits par la relativité générale entrent en ligne de compte.
2. Comment cette situation peut-elle être obtenue ? Supposons que les deux jumeaux sont initialement relativement éloignés de la planète, ainsi un des jumeaux reste presque immobile tandis que l'autre animé d'une certaine vitesse initiale vers la planète s'en approche et fait alors demi-tour. Ce n'est pas si simple ! Il faut que sa vitesse initiale soit faible pour ne pas échapper à l'attraction de la planète et s'en aller sans faire demi-tour. Et si elle est faible, l'autre jumeau aura le temps lui aussi d'être attiré.

En fait, ces deux arguments ne suffisent pas ! En effet, les effets gravitationnels sont assez faibles sur la marche des horloges, bien que non négligeables (nous ne le montrerons pas ici car c'est le domaine de la relativité générale). A moins d'invoquer des corps extrêmement massifs comme des trous noirs ou des étoiles à neutrons.

Et s'il est difficile de trouver une configuration où les deux jumeaux sont en chute libre et se rencontrent à nouveau, ce n'est pas impossible.

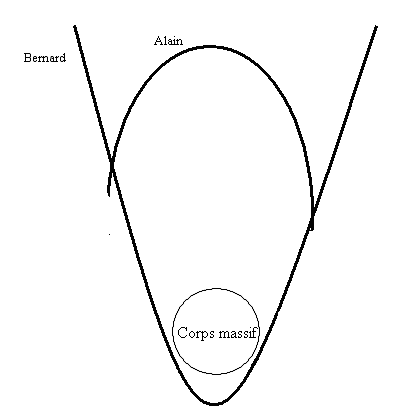
Par exemple Alain peut parcourir une ellipse à faible vitesse (comme une planète autour du soleil) et Bernard une hyperbole à grande vitesse près de la planète (comme une comète). On peut calculer les paramètres de ces deux orbites de façon à ce que Alain et Bernard se rencontrent aux points de croisement. Ce genre de situation n'est pas si exceptionnelle, pensons par exemple à la comète Shoemaker-Levy 9 qui, après avoir frôlé la planète Jupiter, est revenue percuter cette dernière après avoir contourné le Soleil.

Evidemment même dans ce cas les effets relativistes seront assez faibles à moins à nouveau d'employer un corps extrêmement massif pour obtenir des vitesses notables.

Mais ce n'est pas grave car les effets de la relativité restreinte sont, avec des vitesses orbitales classiques, plus importants que les effets gravitationnels et le paradoxe des jumeaux resurgit.

En réalité, il n'est nul besoin d'invoquer des arguments aussi compliqués. En effet, même si les repères sont inertiels, du point de vue de la relativité restreinte ce qui importe avant tout pour l'utilisation de la théorie, par exemple les transformations de Lorentz, est que les deux repères considérés (Alain et Bernard) appartiennent à la même classe de repères en mouvement relatif de translation uniforme. Si la vitesse relative n'est pas constante, c'est peine perdue. Et ici ce n'est pas le cas.

De plus, l'étude des paradoxes précédents nous a donné tout ce dont nous avons besoin

Pour résoudre ce type de situation, deux approches sont possibles.

1. On se place entièrement dans le cadre de la relativité générale. On regarde l'espace-temps correspondant à la situation, par exemple avec un corps massif une métrique dite de Schwartzchild (elle décrit la géométrie à symétrie sphérique autour d'un corps massif en relativité générale), et on calcule les trajectoires d'Alain et Bernard. Puis on calcule le temps propre par intégration de l'intervalle et le tour est joué.
   C'est une méthode générale semblable à celle utilisée dans le paradoxe des jumeaux classiques mais l'espace-temps n'est plus celui de Minkowski.
   C'est la méthode la plus sûre et la plus précise mais il est vrai qu'elle est compliquée (comme la relativité générale).
2. Dans le cas où l'espace n'est pas trop courbé, ce qui est souvent le cas avec des corps célestes de masse modérée comme la Terre, on peut effectuer l'approximation suivante.
   On considère que l'espace-temps est de Minkowski et un repère attaché au repère géocentrique comme inertiel. Le centre de la Terre est immobile dans ce repère et la Terre tourne dans ce repère.
   Dans cet espace on a des corps en rotation : les satellites et même les gens au sol (la Terre tourne).
   Le choix de ce repère est justifié d'une part par des considérations expérimentales (on vérifie expérimentalement que ce repère est bien inertiel et, par exemple, la rotation de la Terre dans ce repère est physiquement mesurable, par exemple avec la méthode du pendule de Foucault, le pendule oscillant en même temps qu'il tourne sur lui-même en 24 heures à cause de la rotation de la Terre) mais aussi par des considérations théoriques (le cas ci-dessus montre que la distribution des masses, la Terre, le Soleil,... impose la géométrie courbe de la relativité générale et justifie l'existence des repères inertiels comme nous l'avons expliqué plus haut).
   Les satellites en rotation sont considérés tourner non plus à cause de la courbure de l'espace-temps (relativité générale) mais simplement à cause de la force de gravité qui n'est rien d'autre qu'une force centripète.

Bien qu'en réalité le référentiel du satellite soit inertiel, dans cette approximation on considère que ce n'est pas nécessairement le cas et que c'est le repère géocentrique R qui est la référence.

Il faut faire le choix : soit on se place dans le contexte de la relativité générale, les corps sont inertiels, la gravité n'est pas une force mais un effet géométrique, et l'espace-temps est courbe, soit on se place dans une situation newtonienne, les corps sont accélérés (en rotation autour de la planète), la gravité est une force et l'espace-temps dans le repère géocentrique est celui de Minkowski. Mais il ne faut pas mélanger les deux approches ! Elles ont en effet une conception des phénomènes radicalement opposée et même si les deux sont liés, mélanger les torchons et les serviettes n'apporte qu'erreurs et confusion.

On peut alors utiliser les méthodes et calculs appropriés aux différents points de vues : dilatation du temps, effet Sagnac,...

Les situations envisageables sont exactement les mêmes que précédemment et se résolvent de la même manière.

Cette approche est nettement plus simple que la précédente mais elle est approchée en ce qu'elle ne prend pas en compte les corrections relativistes dues à la gravitation (considérée ici comme newtonienne) en relativité générale.

Un exemple typique est celui des GPS. On utilise pour ceux-ci l'approximation décrite dans le second point de vue.

Pour calculer les effets de décalage relativiste des horloges des satellites par rapport aux horloges des stations, on utilise :

• La relativité restreinte. Exactement comme dans le second point de vue. On tient compte de la dilatation du temps dû à la vitesse relative du satellite par rapport à la station. Comme les échanges d'informations se font par onde radio on doit aussi tenir compte des distances entre satellites et de la vitesse des signaux.
  Le point de vue de référence adopté est celui des stations et un très léger effet Sagnac peut donc intervenir, mais il est très faible (bien que mesurable) et sans importance car les calibrages entre satellites et stations au sol se font plus vite qu'un tour complet de satellite.
• On ajoute une correction, beaucoup plus faible que les effets précédents, due à la gravité. Le fait qu'en relativité générale une horloge placée dans un champ gravitationnel marche plus lentement. Donc une horloge en altitude marche plus vite.

Cet effet a déjà pu être vérifié sur une hauteur de l'ordre de 100 m (en utilisant une tour) et donc, bien que faible, il faut en tenir compte sous peine d'avoir une erreur importante pour le calcul de la position GPS.

Ces deux effets sont opposés : la dilatation du temps fait que l'horloge du GPS semble marcher plus lentement par rapport à nous tandis que la gravité fait qu'elle marche plus vite. Le deuxième effet étant nettement plus faible, l'effet net est un retard des horloges des GPS.

Il n'y a pas de calculateur sophistiqué à bord des satellites GPS. Les calculs touchant la relativité ont été effectués en avance, au sol, et les résultats sont inclus sous forme de formules numériques simples dans les petits calculateurs des satellites. Une bonne partie de la correction est déjà incluse dans le rythme des horloges atomiques des GPS, rythme modifié pour inclure une grande partie des effets relativistes. Les horloges vont un peu plus vite que la normale pour compenser les effets de la relativité.