Polynôme minimal d'un nombre algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Outils issus de l'algèbre linéaire
Dans tout ce paragraphe, on suppose que l'extension L est finie et galoisienne.
Théorème de Cayley-Hamilton
L'algèbre linéaire offre de nombreux outils, que la remarque suivante permet d'utiliser : L est un espace vectoriel sur K, l'application φm de L dans L qui à x associe m.x est un endomorphisme. Son polynôme minimal en tant qu'endomorphisme est le même que celui du nombre algébrique m.
Soit P[X] le polynôme minimal de m dans K et K[m] le corps de rupture de P[X] contenant m. Le corps L est un K[m] espace vectoriel soit n sa dimension et (l1, ... ln) une base de L en tant que K[m] espace vectoriel. Tout vecteur l de L s'exprime comme une combinaison linéaire des éléments de la base avec des coefficients dans K[m], c'est-à-dire s'exprimant comme l'image de polynômes de degré inférieur ou égal à d le degré de P[X] :
![\forall l \in \mathbb L,\;\exists P_j[X] \in \mathbb K[X] \quad / \quad l = \sum_{i=j}^nP_j[m].l_j \quad \text{avec}\quad \text{deg } (P_j[X]) < d](https://static.techno-science.net/illustration/Definitions/autres/a/ac31ac1a8919ab7fe527b431ca4c9330_36879f830d21f874d2b1404f897c58cf.png)
On en déduit que la famille (mi.lj) si i varie de 0 à d - 1 et j de 1 à n forme une base de L en tant que K espace vectoriel.
Dans ces bases l'expression matricielle de φm et de sa restriction à K[m] est simple. Soit MK[m] la matrice de la restriction de φm à K[m] dans la base (1, m, ... md-1), on a :
![P[X] = a_0 + a_1X + \cdots + a_dX^d \quad \text{et}\quad M_{\mathbb K[m]}= \begin{pmatrix} 0 & \cdots & \cdots & -a_0 \\ 1 & 0 & \cdots & -a_1 \\ \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & 1 & -a_{d-1} \end{pmatrix}](https://static.techno-science.net/illustration/Definitions/autres/6/64c40630310d0401338a40a657714788_6dc2b8f4bcaab6b3b42d15064ba84706.png)
On en déduit la proposition suivante :
-
- Sur son corps de rupture, le polynôme minimal et le polynôme caractéristique de φm sont confondus.
Dans L, on obtient une expression matricielle ML en matrices blocs analogue à la réduction de Jordan, ainsi que celle du polynôme caractéristique χ[X] :
![M_{\mathbb L} = \begin{pmatrix} M_{\mathbb K[m]} & 0 & \cdots & 0 \\ 0 & M_{\mathbb K[m]} & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & M_{\mathbb K[m]} \\ \end{pmatrix}](https://static.techno-science.net/illustration/Definitions/autres/d/da3287f62e30d00b2cc3b6c6da4976f7_e14eccffb423fd47c545b2be723d3ff3.png)
Ce résultat fournit une preuve, dans un cas particulier du théorème de Cayley-Hamilton, ainsi que l'égalité suivante :
![\chi[X] = (-1)^n P^n[X]\quad \text{et}\quad \chi[X] =\prod_{i=1}^d \Big(\sigma_i(m) - X\Big)](https://static.techno-science.net/illustration/Definitions/autres/1/15ed776e357abc06ead9977db77c6607_20db18648b18639bcf5bd834939ab1b4.png)
Ici la famille (σ1, σ2, ..., σd) décrit les éléments du groupe de Galois.
Norme
Dans ce paragraphe L est de dimension finie d en tant que K espace vectoriel, l est un élément de L et φl désigne l'endomorphisme du K espace vectoriel L qui à x associe l.x.
L'algèbre linéaire fournit des outils supplémentaires à la théorie de Galois et à la théorie algébrique des nombres. La norme est un exemple.
La norme relative à L dans K de l correspond au déterminant de l'endomorphisme φl. Elle est en général notée NL/K(l). Avec les notations précédentes, si l'extension est galoisienne, elle vérifie :
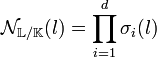
En effet, le déterminant est égal au coefficient constant du polynôme caractéristique calculé précédemment. Par définition, elle prend ses valeurs dans K.
A la différence de la norme relative, la norme est indépendante de l'extension. Elle correspond au déterminant précédent si L est le corps de rupture de l. Si D est le corps de décomposition de l et si G désigne son groupe de Galois, l'égalité suivante est vérifiée :
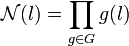
Les résultats précédents montrent que si n est la dimension de D en tant que L espace vectoriel, la norme à la puissance n est égale à la norme relative. La norme est aussi un élément de K.
Forme trace
La trace est une application un peu de même nature que la précédente. La trace de L sur K de l'élément l est égal à la trace de l'endomorphisme φl. La trace d'un élément l est donc égale au coefficient sous dominant du polynôme minimal. L'application qui à deux éléments a et b de L associe la trace de a.b est appelée forme trace. Elle joue un rôle important en théorie algébrique des nombres, par exemple pour définir le discriminant.

















































