Polynôme minimal d'un nombre algébrique - Définition

Contexte

Motivation

Évariste Galois est à l'origine d'une théorie mettant en évidence les conséquences des propriétés des polynômes minimaux.

En 1801, Carl Friedrich Gauss étudie le polynôme minimal à coefficients rationnels de la racine n^ième de l'unité dans le corps des complexes et lui donne le nom de polynôme cyclotomique. Cette approche est fructueuse, l'étude de son degré ainsi que des opérations réalisables sur les racines mettent en évidence des propriétés de ces racines. Il en conclut par exemple que l'heptadécagone, c'est-à-dire le polygone régulier à 17 côtés est constructible à la règle et au compas.

Cette approche est généralisée par Évariste Galois . Il étudie systématiquement les extensions K contenant toutes les racines d'un polynôme irréductible P[X] à coefficients rationnels. Un tel polynôme est le polynôme minimal de chacune des racines. Il étudie ainsi le problème de l'extraction de racine par radical (c'est-à-dire une racine n^ième d'un rationnel) d'un polynôme irréductible.

En termes contemporains, une telle démarche permet de disposer de résultats provenant de quatre structures algébriques différentes. Le corps K peut être vu comme un espace vectoriel, si k est un élément du corps, l'application de K dans K, qui à x associe k.x est un endomorphisme de K, vu comme un Q espace vectoriel, son polynôme minimal au sens des endomorphisme correspond au polynôme minimal de l'entier algébrique k, l'algèbre linéaire est disponible avec une telle approche. Il est relativement facile de constater que tout automorphisme de K permutent les racines de P[X], ils forment donc un groupe fini isomorphe à un sous-groupe des permutations des racines. Un tel groupe porte le nom de groupe de Galois et la théorie des groupes offrent des théorèmes pour mieux comprendre une telle structure. Enfin, l'anneau des polynômes à coefficients dans Q dispose de propriétés fortes, il est par exemple euclidien. Cette richesse permet à Galois d'offrir une nouvelle formulation du théorème d'Abel, donnant une condition nécessaire et suffisante pour qu'un polynôme soit résoluble par radical.

Le polynôme minimal est à l'origine de la définition de K, il dispose de nombreuses propriétés provenant de l'algèbre linéaire, des propriétés du corps K ou encore du groupe de Galois.

Théorie algébrique des nombres

Leonhard Euler est un précurseur. Il comprend l'intérêt de nombres ayant un polynôme minimal à coefficients entiers. Une maitrise insuffisante des structures maintenant appelées anneau conduit néanmoins à glisser une erreur dans sa démonstration.

L'intérêt pour le polynôme minimal possède aussi une autre origine. La résolution de certaines équations diophantiennes comme celle des deux carrés est simplifiée si un nouvel anneau est utilisé. Gauss découvre à cette occasion les entiers portant maintenant son nom. Ils correspondent aux complexes de la forme α + i.β, où α et β sont des entiers naturels. Si p est un nombre premier congru à 1 modulo 4, alors il existe un morphisme de l'anneau des entiers de Gauss, vers Z/pZ. Le noyau de ce morphisme est un idéal principal de générateur un nombre α + i.β tel que α² + β² est égal à p, ce qui permet de résoudre l'équation.

Une démarche de cette nature possède un célèbre antécédent, Leonhard Euler utilise les nombre de la forme α + i√3.β pour tenter de démontrer le dernier théorème de Fermat pour n = 3. Il annonce à Goldbach en 1753 qu'il a enfin trouvé une solution. Elle se révèle fausse, il suppose implicitement que l'anneau considéré est euclidien. Ce n'est pourtant pas le cas, comme le montre l'égalité suivante :

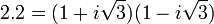
Les trois nombres utilisés n'ont pas de diviseurs autre que 1 ou le nombre lui-même (à un nombre inversible près). Ferdinand Eisenstein finit par trouver le bon anneau d'entiers équivalent, il est formé des nombres de la forme α + j.β où j désigne une racine cubique de l'unité.

La bonne définition d'un entier algébrique d'une extension finie de Q est celle des nombres dont les coefficients du polynôme minimal sont des entiers naturels. Cet ensemble forme un anneau. Si dans le cas général, il n'est pas euclidien, il possède néanmoins suffisamment de propriétés pour permettre de bâtir une théorie. L'anneau est dit de Dedekind. Si l'anneau n'est en général ni euclidien ni factoriel, le passage à la notion d'idéal fractionnaire montre que tout idéal est le produit, d'une manière unique d'idéaux premiers. Cette propriété est fondatrice de la théorie algébrique classique des nombres, elle remplace la décomposition en facteurs premiers perdue dans le cas général.

Le polynôme minimal est ainsi l'outil de définition d'un entier algébrique. Ses propriétés, dérivées de l'arithmétique, l'algèbre linéaire et la théorie de Galois, sont utilisées pour établir les théorèmes clé de la théorie comme celui de Dirichlet ou celui sur le groupe des classes d'idéaux.