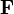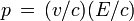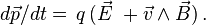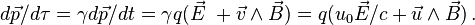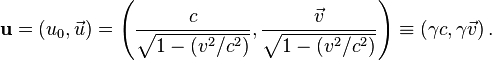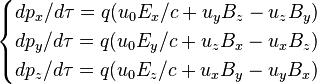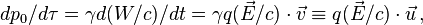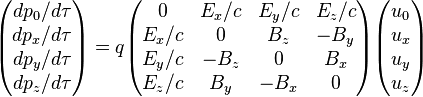Relativité restreinte - Définition

Cas des particules de masse nulle

Les donnant E et p en fonction de m et v conduisent immédiatement à la formule

Si la vitesse de la particule est égale à la vitesse de la lumière, alors p = E / c en calculant E² − p²c² on voit que la masse de la particule est forcément nulle. En sens inverse, si la masse de la particule est nulle, alors p = E / c et par conséquent v = c.

Nous aboutissons donc à la conclusion double importante selon laquelle les particules matérielles ne peuvent pas atteindre la vitesse de la lumière et que seules des particules sans masse se déplacent à la vitesse de la lumière.

L'ensemble est parfaitement cohérent : tout mécanisme de propagation d'énergie à la vitesse de la lumière correspond à une quantité de mouvement p égale à l'énergie et donc à une « masse au repos » nulle. En sens inverse, une particule de masse nulle se déplace forcément à la vitesse de la lumière.

La non-conservation de la masse

La conservation du quadrivecteur énergie-impulsion explique que dans une réaction la masse d'un système puisse ne pas se conserver pour se transformer en énergie, en partie ou en totalité. C'est ce qui se passe dans les réactions de fission, de fusion et d'annihilation de particules.

Fission spontanée d'une particule

Supposons qu'un corps au repos, de masse M, se désintègre spontanément en deux parties de masses (masses au repos) respectives et  : on montre qu'alors la masse M est supérieure à et que la différence prend la forme d'une énergie cinétique.

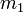
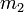
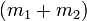
La loi de conservation de l'énergie donne car , et donc .

Dans le cas où , cette désintégration ne peut pas être spontanée, elle ne peut se réaliser qu'après apport d'une énergie au moins égale à son « énergie de liaison » égale à .

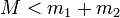
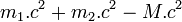
La loi de conservation de l'impulsion donne , donc , d'où on tire .

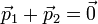
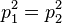
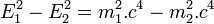
Finalement, les égalités et permettent de déterminer les énergies des deux nouvelles particules : et . La différence de masses s'est convertie en énergie cinétique pour les deux nouvelles particules, énergie que l'on retrouve dans et .

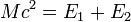
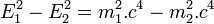
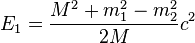
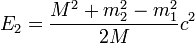
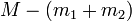
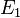
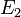
On peut également calculer la norme des impulsions des deux particules, et donc aussi de leurs vitesses.

Une fission de particule implique aussi la conservation de nombres quantiques : la charge électrique, le spin, etc.

Électromagnétisme et relativité restreinte

Dans l'espace newtonien à trois dimensions, une particule de charge q placée dans un champ électrique et un champ magnétique est soumise à la force de Lorentz et l'équation qui régit son mouvement est

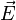
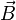
Pour transposer cette formule en mécanique relativiste, on devra considérer le quadrivecteur énergie-impulsion à la place du vecteur et évaluer le taux de variation de ce quadrivecteur non dans le référentiel d'un observateur galiléen quelconque mais dans le référentiel propre de la particule. Le membre de gauche sera donc de la forme , où τ est le de la particule chargée. À droite on trouvera un objet indépendant du référentiel choisi et qui en outre sera forcément une fonction linéaire de la vitesse de la particule. En effet la partie spatiale de l'équation de la dynamique est linéaire en puisqu'elle s'écrit

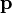
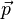
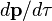
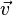
Dans cette expression et sont les composantes dans un référentiel lorentzien du quadrivecteur vitesse , lequel peut donc s'écrire :

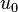
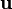
De façon explicite l'équation ci-dessus se décompose sur les trois axes de la façon suivante :

De son côté la composante temporelle de l'équation de la dynamique (qui correspond à la loi donnant la variation de l'énergie) s'écrit

où W est le travail de la force

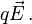
En rassemblant les équations écrites ci-dessus dans le cadre d'un espace-temps à quatre dimensions, le taux de variation du quadrivecteur énergie-impulsion est donné par

L'équation matricielle que nous venons d'écrire montre qu'en relativité restreinte le champ magnétique et le champ électrique constituent une entité unique. En réalité la présentation précédente est quelque peu incorrecte dans la mesure où pour tirer parti de toute la puissance de la théorie relativiste il est nécessaire de faire appel aux tenseurs. L'équation matricielle ci-dessus est la traduction en termes de composantes de l'équation tensorielle, indépendante, elle, de tout système de coordonnées

est le tenseur du champ électromagnétique (ou tenseur de Maxwell ou tenseur de Faraday). C'est cet objet qui représente physiquement le champ électromagnétique. Ses composantes dans un certain système de coordonnées sont données par la matrice écrite ci-dessus.