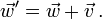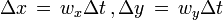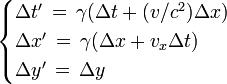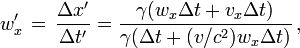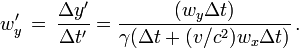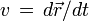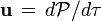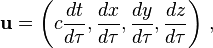Relativité restreinte - Définition

Vitesse et quadri-vitesse

Loi de composition des vitesses

Dans une fusée se déplaçant à la vitesse par rapport à la Terre on tire un boulet de canon à la vitesse mesurée dans la fusée. Quelle est la vitesse du boulet mesurée sur Terre ?

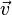
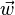
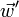
En cinématique galiléenne les vitesses s'ajoutent et on aurait

En cinématique relativiste la loi de composition des vitesses est différente :

En supposant que on écrit et

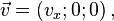
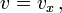
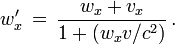
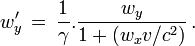
Cette relation montre que la loi de composition des vitesses en relativité restreinte n'est plus une loi additive et que la vitesse c est une vitesse limite quel que soit le référentiel considéré (quand on lui ajoute une vitesse, on retombe sur c).

Cependant, dans le cas où les deux vitesses et sont parallèles, il existe un paramétrage permettant d'obtenir une loi additive. Il suffit pour cela de passer de la vitesse v au paramètre angulaire de vitesse θ introduit , et appelé rapidité.

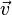
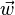
Montrons que dans une composition de vitesses les paramètres angulaires de vitesse s'ajoutent.

En posant , , et en utilisant la formule d'addition des fonctions hyperboliques , on trouve

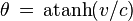
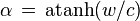
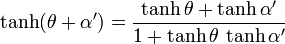
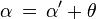
Le paramètre angulaire correspondant à la vitesse c est infini puisque artanh(x ), l'argument tangente hyperbolique de x, tend vers l'infini lorsque x tend vers 1. On retrouve donc le fait que c est une vitesse limite indépendante du référentiel choisi. Cette vitesse limite est impossible à atteindre pour une particule massive, seules les particules de masse nulle, comme le photon, peuvent se déplacer à la vitesse de la lumière.

Application numérique

Imaginons qu'un obus soit tiré avec la vitesse w'  = 0,75c dans le référentiel d'une fusée se déplaçant elle-même à la vitesse v = 0,75c par rapport à la Terre. Quelle est la vitesse du boulet mesurée sur Terre ? Clairement la valeur 1,5c que nous donnerait la formule galiléenne est fausse puisque la vitesse obtenue dépasserait celle de la lumière. Les formules relativistes nous invitent à procéder comme suit. L'angle paramétrique de vitesse de l'obus par rapport à la fusée est L'angle paramétrique de la vitesse de la fusée par rapport à la Terre a la même valeur La rapidité de l'obus par rapport à la Terre est donc , ce qui correspond à la vitesse

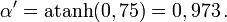
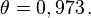
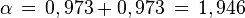
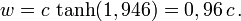
On peut évidemment retrouver ce résultat directement sur la formule donnant w en fonction de w ’ et v.

Le quadrivecteur vitesse

En mécanique newtonienne on étudie le mouvement d'un mobile en suivant sa position en fonction du temps t, ce temps étant supposé de caractère absolu, indépendant de l'horloge qui le mesure. En relativité on abandonne cette vision des choses pour considérer le mouvement d'une particule comme une succession d'événements , la courbe décrite par cet événement dans un espace à quatre dimensions (trois pour l'espace, une pour le temps) prenant alors le nom de « ligne d'univers ».

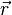
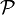
De même qu'en mécanique classique on définit la vitesse d'une particule en prenant la dérivée

de la position par rapport au temps, de même en mécanique relativiste on définit le vecteur vitesse à quatre dimensions (ou quadrivecteur vitesse)

où est le temps propre de la particule, défini .

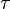
En explicitant les composantes de ce quadrivecteur dans un référentiel donné on peut écrire

expression dans laquelle nous avons introduit le facteur c pour travailler avec des coordonnées homogènes.

Il existe une relation simple, et importante, relative à ce quadrivecteur. La définition du carré de l'intervalle d'espace-temps défini peut se généraliser à tout quadrivecteur. On définira ainsi le carré de la norme d'un quadrivecteur comme la différence entre le carré de sa partie temporelle et celui de sa partie spatiale. Et le résultat capital est que cette norme est invariante par transformation de Lorentz. Autrement dit elle ne dépend pas du référentiel choisi. Dans le cas de la vitesse ce résultat prend une forme particulièrement simple. En effet, dans le référentiel propre de la particule, la partie spatiale du quadrivecteur vitesse est nulle tandis que la partie temporelle vaut tout simplement c (dt/dτ = 1 puisque le temps t est précisément le temps τ tel qu'il est mesuré dans le référentiel du mobile). Autrement dit dans le référentiel propre d'une particule, le quadrivecteur vitesse a pour composantes (c, 0, 0, 0). Par conséquent dans tout référentiel galiléen on aura la relation

(partie temporelle de )² -  (partie spatiale de )² = c² .

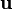
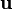
C'est l'invariance de cette norme qui permet de parler du quadrivecteur d'une particule indépendamment de tout système de coordonnées.