Représentations d'un groupe fini - Définition

Introduction par l'exemple

Groupe symétrique d'indice trois

Représentation de S₃ comme groupe des isométries du triangle

La première question associée à la théorie est la recherche d'un ensemble d'applications linéaires inversibles, que l'on associe aux éléments d'un groupe fini G. Dans cet exemple G est le groupe des permutations d'un ensemble à trois éléments noté S₃. L'association φ entre les éléments du groupe et les applications linéaires doit respecter la loi du groupe. Si g et h sont deux éléments du groupe, l'application linéaire associée à g.h doit être la composition des applications associées à g et à h :

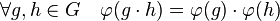
On parle de morphismes de groupe. L'exemple le plus simple est l'application qui, à n'importe quel élément, associe l'application linéaire identité. Cette association est manifestement une représentation, mais elle n'apporte que peu d'intérêt, on parle de représentation triviale. Un deuxième cas associe à un élément de S₃, 1 si la permutation est une transposition et -1 sinon, cette représentation porte le nom de signature. L'espace vectoriel est encore de dimension 1.

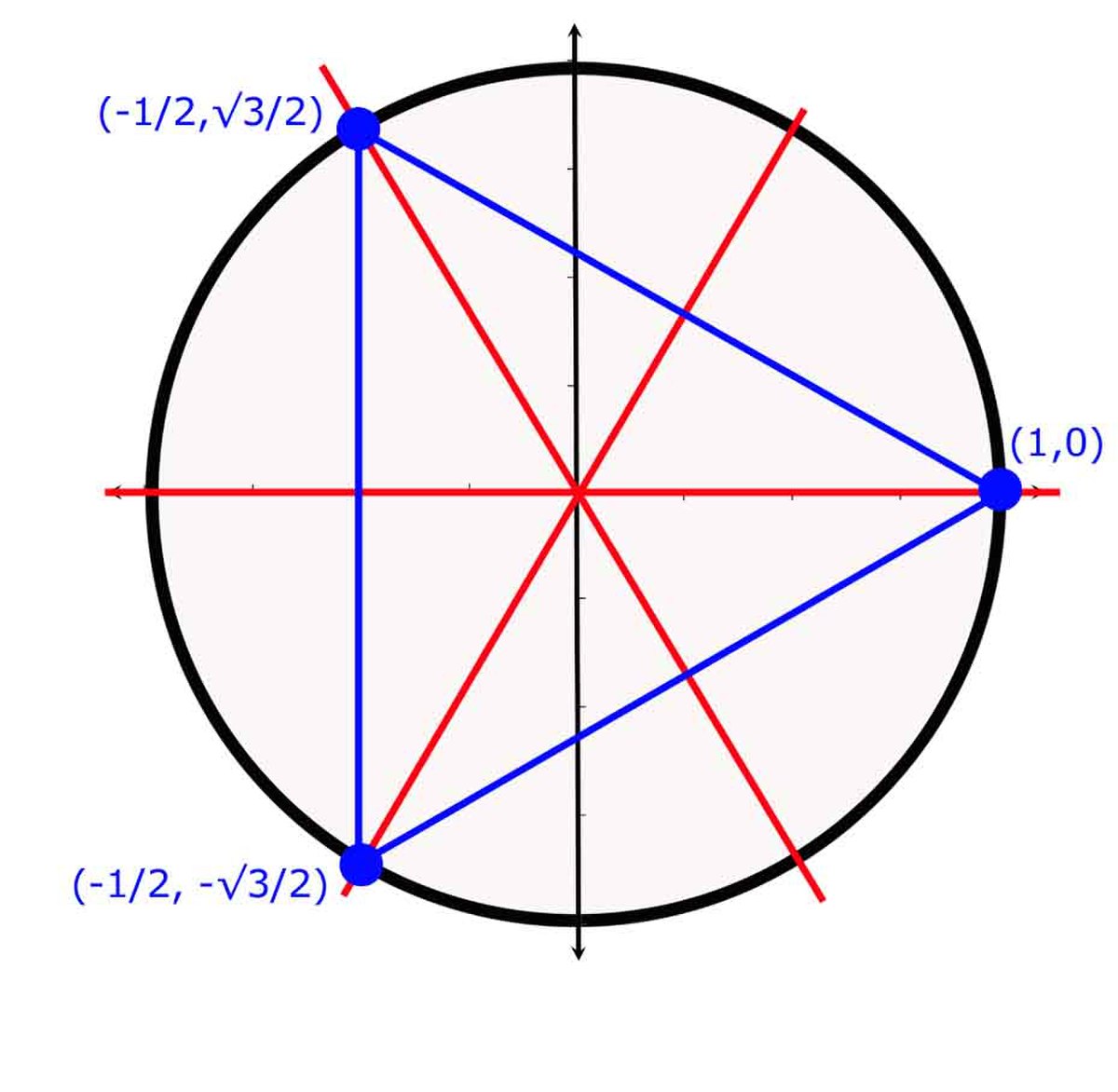
Le troisième cas est illustré sur la figure de droite. L'espace vectoriel est de dimension 2 et équipé d'un produit scalaire. On considère trois vecteurs i, j et k, de norme 1, et faisant chacun un angle de π/3 avec les deux autres. Le groupe S₃ opère sur ces trois vecteurs, c'est-à-dire qu'une permutation g du groupe peut s'appliquer à l'ensemble de ces trois vecteurs, ce qui définit une application de l'ensemble {i, j, k} dans lui-même. Il existe une unique manière de prolonger ces applications en applications linéaires de E et toutes ses applications linéaires sont inversibles. On a ainsi défini une troisième représentation. À la différence des deux autres, celle-ci est fidèle, c'est-à-dire qu'à deux éléments de G distincts on associe deux applications linéaires différentes. En un sens, le groupe formé par les applications linéaires est une copie de S₃, on parle alors d'isomorphisme de groupe.

On remarque que chacune des représentations étudiées concerne uniquement des isométries, ou encore des applications linéaires qui conservent les distances et les angles. La théorie indique qu'il est toujours possible de munir l'espace vectoriel sur lequel agissent les applications linéaires d'un produit scalaire tel que ce soit le cas.

Une quatrième représentation est importante car la technique utilisée est applicable à tous les groupes finis. On note {a_i} pour i variant de 1 à 6, les différents éléments de S₃ et l'on considère ces éléments comme une base orthonormale d'un espace vectoriel de dimension 6. On définit l'association φ(a_i) comme l'application linéaire qui à la base (a₁, ..., a₆) associe la base (a_i.a₁, ...,a_i.a₆). L'image d'une base orthonormale par cette application linéaire est une base orthonormale, les applications linéaires sont donc des isométries. Cette représentation porte un nom, c'est la représentation régulière du groupe. Elle est un peu plus complexe, l'espace vectoriel est de dimension 6, il faut donc 6 matrices 6x6 pour la représenter. Il est utile de la factoriser, c'est-à-dire que trouver des sous-espaces vectoriels stables par toutes les applications linéaires de la représentation et dont la somme directe soit égal à l'espace entier. Sur chacun des sous-espace, la représentation est plus petite, donc plus simple. On trouve de fait une décomposition en 4 sous-espaces, deux de dimension 1 et deux de dimension 2. Sur celles de dimension 1, on trouve une fois la représentation triviale et une fois la signature. Sur celles de dimension 2, on trouve chaque fois, à un isomorphisme près, la représentation de dimension 2 déjà évoquée dans ce paragraphe.

Ce cas particulier est relativement simple, il fut résolu avant l'apparition de la théorie des représentations par une approche calculatoire. Des démonstrations modernes et non calculatoires sont présentes dans l'article associé.

Groupe symétrique d'indice quatre

Représentation de S₄ comme groupe des rotations du cube.

L'origine des représentations provient de la théorie de Galois. Un objet caractéristique de cette théorie est un polynôme, qui, pour rester simple, est choisi ici à coefficients dans les nombres rationnels, par exemple P(X) = X⁴ + X + 1. L'axe d'analyse de la théorie de Galois est celui de l'étude du plus petit corps K contenant toutes les racines de P(X), il est appelé corps de décomposition et peut être considéré comme un sous-corps de C, l'ensemble des nombres complexes. Connaître la structure de ce corps revient à connaître celle de son groupe des automorphismes, encore appelé groupe de Galois. Il correspond à l'ensemble des bijections de K, qui respectent à la fois les additions et les multiplications. C'est toujours un groupe fini.

Ces résultats ne terminent pas la question, la détermination du groupe de Galois est une question souvent difficile. Une manière de l'appréhender est de considérer K comme un espace vectoriel sur le corps des nombres rationnels, chaque élément du groupe apparaît alors comme un ensemble de matrices et ce groupe de matrices est une copie du groupe de Galois. Cette direction de recherche débouche immédiatement sur une complexité calculatoire nécessitant des outils théoriques pour aboutir à des théorèmes. Cette difficulté est illustrée par l'exemple du polynôme P(X). Le groupe de Galois est représenté par 24 matrices 24x24, ce qui fait beaucoup de coefficients à manipuler pour un groupe qui s'avère être S₄, le groupe des permutations d'un ensemble à quatre éléments.

La bonne technique consiste encore en une factorisation, c'est-à-dire la recherche d'une décomposition du gros espace de dimension 24 en une somme directe de plus petits sous-espaces vectoriels qui soient stables par chaque application linéaire du groupe. Dans un premier temps, on cherche les représentations non factorisables, c'est-à-dire qui ne contiennent aucun sous-espace vectoriel stable par toutes les applications linéaires du groupe, on les appelle des représentations irréductibles. Elles sont des facteurs potentiels dans la décomposition de la grosse représentation de dimension 24, on démontre que chaque facteur irréductible est représenté autant de fois que la dimension de son espace vectoriel, dans la grosse représentation.

Il existe 5 représentations irréductibles, finalement pas si difficiles à expliciter. Les deux premières sont la représentation triviale et la signature, chacune de dimension 1. Pour trouver la troisième, il suffit de remarquer que S₄ possède un sous-groupe distingué copie du groupe de Klein. Le quotient des deux groupes est égal à S₃. Il existe une représentation de dimension 2, qui à chaque élément de S₄, associe la représentation de sa classe si cet élément est quotienté par le groupe de Klein. Cette représentation correspond à celle de S₃ déterminée au paragraphe précédent.

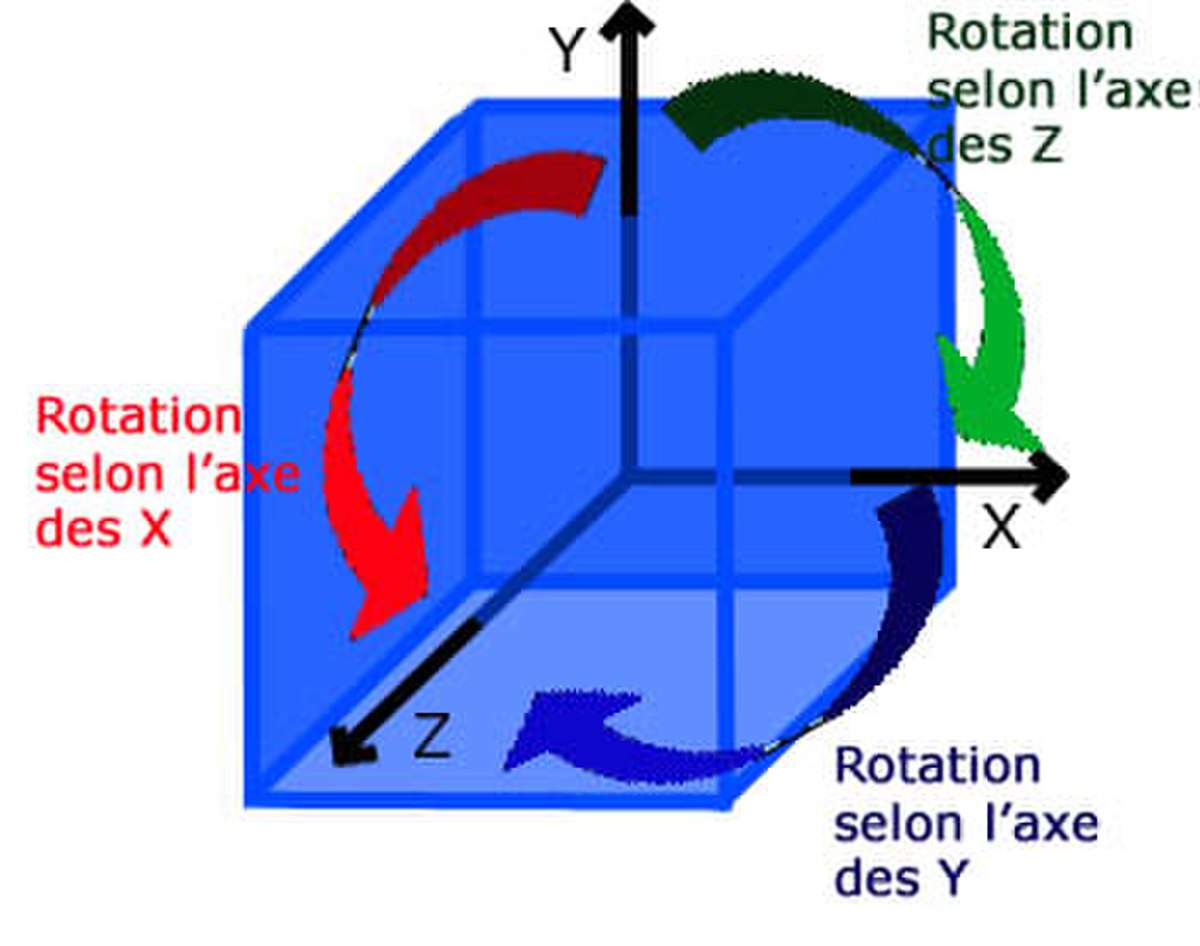
La quatrième s'obtient en considérant un espace de dimension 4 ayant une base orthonormale (e_i) pour i variant de 1 à 4. On associe à g, un élément de S₄, l'application qui à la base associe la même base, mais cette fois permutée par g. Cette application se prolonge en une isométrie. Ce n'est pas encore la bonne représentation car elle contient une copie de la représentation triviale, mais l'orthogonal du sous-espace vectoriel de la représentation triviale est celle recherchée. Elle correspond au groupe des rotations du cube, illustré à droite. La dernière est simplement le produit de cette représentation et de la signature.