Représentations d'un groupe fini - Définition

Usages

Théorie de Galois

La théorie de Galois, peut se voir comme l'étude des relations algébriques qui lient les différents éléments d'un corps commutatif, c'est-à-dire un ensemble muni d'une addition et d'une multiplication tel que tout élément non nul est inversible et tel que les deux opérations soient commutatives. La théorie dite classique s'intéresse aux corps pas trop gros, qui se représentent comme un espace vectoriel de dimension finie sur un corps initial. Un exemple simple est donnée par les nombres de la forme a + b.i, ou a et b sont deux rationnels et i l'unité imaginaire. On parle d'extension quadratique, l'exemple précédent est celui des rationnels de Gauss. L'un des succès originaux de la théorie est d'indiquer quand une équation polynômiale est résoluble par radicaux, c'est-à-dire quand il est possible d'exprimer la racine d'un polynôme à l'aide des quatre opérations et de l'opération racine.

Un résultat clé de la théorie stipule que la structure d'un corps L est décrite par la correspondance de Galois. Elle porte sur un groupe particulier, dit de Galois, celui des bijections de K dans K qui respectent les deux opérations du corps. Le groupe de Galois des rationnels de Gauss comporte deux éléments, l'identité et l'application conjuguée. Si les rationnels de Gauss sont vus comme un espace vectoriel de dimension 2, avec comme base (1, i) le groupe de Galois peut être vu comme une représentation d'un groupe à deux éléments. Pour plus de simplicité, on peut incarner le groupe de Galois par des matrices, puis considérer ces matrices à coefficients dans les rationnels, comme celles d'applications linéaires sur un espace vectoriel complexe, ce qui est beaucoup plus simple à étudier.

Disposer d'une théorie comme celle de la représentation d'un groupe fini pour étudier le groupe de Galois s'avère rapidement indispensable. On peut citer comme exemple celui du théorème d'Abel sur la possibilité de résoudre une équation polynomiale par radical. Sous sa forme galoisienne, ce résultat s'exprime par le fait que l'équation est résoluble si et seulement si le groupe de Galois possède une propriété particulière. On dit alors que le groupe est résoluble. Le théorème de Burnside sur cette question, décrit dans paragraphe précédent est ainsi typiquement galoisien.

Théorie algébrique des nombres

L'usage des représentations et des caractères des groupes abéliens finis, fait son apparition en arithmétique bien avant les travaux de Frobenius. Un important théorème, dit de la progression arithmétique, démontrée par Dirichlet utilise des caractères de cette nature.

Le cas non abélien, au cœur de la théorie présentée dans cet article, n'est pas en reste. La structure étudiée par la théorie algébrique des nombres est très liée à la théorie de Galois. Une manière simple de voir cette structure est de ne considérer que les entiers algébriques d'un corps de la même nature que ceux du paragraphe précédent. Un entier algébrique est un élément de ce corps racine d'un polynôme unitaire (c'est-à-dire dont le coefficient du monôme de plus haut degré est égal à 1) et à coefficients dans les entiers relatifs. Les entiers algébriques des nombres rationnels sont les entiers relatifs, ceux des rationnels de Gauss sont les nombres de la forme a + i.b, où cette fois a et b sont des entiers relatifs.

Une fois encore le groupe des bijections respectant l'addition et la multiplication, on parle d'automorphisme d'anneau, s'avère essentiel. On parle toujours de groupe de Galois. Une démarche de la même nature que celle du paragraphe précédent permet d'associer à ce groupe, une représentation naturelle. Cette représentation est importante pour comprendre les idéaux d'un anneau d'entiers algébriques. Les idéaux sont un être mathématique découvert par Ernst Kummer pour résoudre le dernier théorème de Fermat dans de nombreux cas. Si les anneaux d'entiers algébriques ressemblent, à beaucoup d'égards, aux entiers relatifs, le théorème fondamental de l'arithmétique stipulant l'existence et une forme d'unicité d'une décomposition en facteurs premiers ne s'applique plus. Ce que Kummer appelait des nombres idéaux est une manière de pallier cette lacune, les idéaux premiers remplaçant les nombres premiers (cf l'article Idéal fractionnaire).

Bien comprendre la manière dont se structurent les idéaux est un facteur déterminant pour résoudre des problèmes d'arithmétique. Le groupe de Galois est important car l'image d'un idéal par un élément du groupe est encore un idéal. D'une certaine manière, la structure du groupe se reporte sur des classes d'idéaux. Un exemple d'usage est l'équation de Pell-Fermat. Si elle semble simple, sa résolution s'avère redoutable. Elle correspond à l'équation diophantienne suivante :

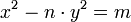
Une équation diophantienne est une équation à coefficients dans les nombres entiers où les solutions recherchées sont entières. Ici n est un entier non carré parfait et m un entier différent de zéro. Dans le cas général, cette équation est résolue par David Hilbert à l'aide d'une première ébauche de la théorie des corps de classe. La connaissance du groupe de Galois, souvent obtenue par l'étude de la représentation naturelle, est le nœud de la démonstration. La recherche arithmétique actuelle fait toujours grand usage des représentations d'un groupe fini. Un exemple archétypal est un prolongement de la théorie des corps de classe dans le cas non commutatif. Il porte le nom de programme de Langlands. Une fois encore les représentations sont indispensables.

Algèbre non commutative

La théorie de Galois, à travers les corps de solutions d'une équation algébrique ou son anneau des entiers algébriques, est capable de fournir de nombreux exemples d'ensembles munis d'une addition et d'une multiplication. Ces structures ont toutes un élément commun, la multiplication est commutative.

Les mathématiques, comme les sciences de la nature, mettent en évidence des cas où la multiplication n'est pas commutative. Beaucoup d'ensembles de matrices, sont naturellement munis de ces deux opérations et disposent d'une multiplication qui ne l'est pas. William Hamilton passe dix ans de sa vie pour trouver un ensemble de cette nature capable de formaliser plus simplement la mécanique newtonienne. Il découvre à cette occasion le premier corps gauche, c'est-à-dire un ensemble tel que tous les éléments non nuls sont inversibles, mais qui n'est pas commutatif appelé quaternion.

L'exemple des corps est significatif de l'apport de la représentation des groupes finis dans cette branche des mathématiques. On peut remarquer dans un premier temps que le plus petit sous-corps d'un corps gauche L est nécessairement commutatif. L apparaît alors comme un espace vectoriel sur K. Le plus petit sous-corps n'est pas l'unique candidat, par exemple le corps des quaternions est un espace vectoriel de dimension 4 sur les nombres réels. Si L est un espace vectoriel de dimension finie sur K, il est possible d'isoler dans L un petit groupe multiplicatif G fini suffisamment vaste pour que l'espace vectoriel sur K engendré par le groupe soit le corps L. Cette méthode permet de voir L comme une conséquence d'une représentation de G. Une approche analogue est utilisée pour construire les quaternions dans l'article représentations du groupe des quaternions.

D'une manière plus générale, considérer une représentation comme une algèbre d'un groupe fini est une méthode puissante pour étudier une famille d'anneaux dits semi-simples et contenant de nombreux représentant non commutatifs. Le théorème central de cette théorie porte le nom d'Artin-Wedderburn.

Réseau

La structure d'un cristal s'analyse à travers la représentation d'un groupe fini. Il correspond au groupe orthogonal du réseau associé. Celui-ci est un cristal de dravite.

Un réseau est un groupe discret de Rⁿ, générateur de l'espace vectoriel. Une question qui se pose est celle du groupe orthogonal, c'est-à-dire l'ensemble des isométries linéaires, d'une telle structure. On montre assez simplement qu'un tel groupe est fini et dans le cas de la dimension 2, les outils élémentaires de la théorie des groupes et de l'algèbre linéaire permet d'élucider cette question. En revanche, quand la dimension augmente les outils associés à la représentation d'un groupe fini, particulièrement les caractères, s'avèrent indispensables.

Le cas de la dimension 3 intéresse particulièrement les cristallographes. Un cristal se modélise par un réseau, auquel cette science donne le nom de Bravais. Cette géométrie est à l'origine de propriétés mécaniques, optiques ou encore électriques. A travers les tables de caractères, il est possible de déterminer le groupe orthogonal, qui, dans ce contexte, prend le nom de groupe de symétrie ou groupe ponctuel.

Une question analogue, aussi en dimension 3, se traite aisément avec les outils des représentations d'un groupe fini, celui des solides de Platon. Ils correspondent aux polyèdres réguliers convexes d'un espace de dimension 3. L'analyse de groupes admettant une représentation irréductible de dimension 3 permet d'établir l'existence et les caractéristiques des différents solides de Platon. Les exemples du tétraèdre, du dodécaèdre et de l'icosaèdre sont traités dans l'article groupe alterné.

Les dimensions plus élevées sont l'objet d'études de la part des cryptologues. Si la dimension augmente, la recherche du plus petit vecteur non nul est un problème conjecturé comme difficile. Difficile prend ici un sens très précis. Il ne signifie pas que personne ne sait le résoudre, mais que les seules méthodes accessibles, avec la vitesse actuelle (2008) des ordinateurs, demande beaucoup de temps, typiquement un temps supérieur à l'age de l'univers. Un des codes assurant une des meilleures sécurité est fondé sur la géométrie d'un réseau de cette nature, il porte le nom de NTRU.

Classification des groupes finis

La théorie des représentations est l'un des outils essentiels pour la classification des groupes. Pour les groupes d'ordre petit, les théorèmes de Sylow suffisent en général. En revanche, cette approche est trop limitée pour une étude générale. Les théorèmes de Burnside, sur le cardinal d'un groupe résoluble ou sur les groupes d'exposant fini et de type fini sont des exemples caractéristiques. On trouve des cas d'utilisations un peu élémentaires de la théorie, par exemple pour établir le caractère simple d'un groupe d'ordre 168.

Une des techniques, pour élucider la structure d'un groupe fini un peu complexe est de considérer sa représentation en tant que groupe orthogonal d'un réseau. Un exemple est le réseau de Leech, de dimension 24, son groupe orthogonal permet de mettre en évidence les groupes de Conway, dont le plus grand, généralement noté CO₁, comporte 4 157 776 806 543 360 000 éléments. C'est un groupe sporadique obtenu par quotient du groupe orthogonal par son centre.

Le plus célèbre cas est probablement le groupe Monstre, le plus gros des 26 groupes sporadiques simples. Son existence était annoncée depuis une dizaine d'années avant sa construction. Elle devait découler d'une représentation de dimension 196 883, conjecturé et explicité sans l'aide d'ordinateur. Elle devrait clore la classification des groupes finis simples.