Représentations d'un groupe fini - Définition

Représentations, caractères et algèbre de groupe

Représentations d'un groupe

Heinrich Maschke auteur du théorème portant son nom

Une représentation d'un groupe G d'ordre fini est la donnée (V, ρ) d'un espace vectoriel de dimension fini et d'un morphisme ρ de G dans l'ensemble GL(V) des automorphismes de V. On obtient les propriétés suivantes :

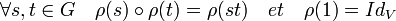
Comme le montrent les exemples précédents, une représentation peut apparaître de manière complexe. Le premier objectif est de la réduire par la recherche de sous-représentations. Une sous-représentation est la donnée d'un sous-espace vectoriel de V stable par chaque image de ρ. Si de tel sous-espace n'existe pas (à part l'espace vectoriel nul et l'espace entier V) on parle de représentation irréductible.

Il existe un résultat important, appelé théorème de Maschke annonçant que si la caractéristique du corps est première avec l'ordre du groupe G, alors l'espace V est somme directe de sous-espace irréductibles. La situation décrite dans les deux exemples n'est pas une exception.

Cette situation est différente, par exemple, de celle de la réduction d'endomorphisme. En dimension 2, un endomorphisme nilpotent d'ordre deux possède un noyau, qui comme tout noyau est stable par l'endomorphisme. Cependant il n'existe pas de supplémentaire stable, car tout supplémentaire est envoyé par l'endomorphisme sur le noyau.

Il n'existe qu'un nombre fini de représentations irréductibles pour un groupe fini donné, à un isomorphisme près. Les représentations isomorphes sont en général identifiées dans la théorie. Un isomorphisme τ entre deux représentations (V, ρ) et (V' , ρ') est un isomorphisme d'espace vectoriel de V dans V' tel que :

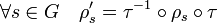
La logique suivie dans les exemples est celle de la théorie. Dans un premier temps, les représentations irréductibles sont déterminées. Une méthode simple permet de connaître le nombre de représentations irréductibles distinctes pour un groupe donné. Ensuite, pour une représentation donnée, une analyse permet de savoir quelles représentations irréductibles la contiennent.

Caractères du groupe

Caractères du groupe symétrique d'indice trois.

Un des deux piliers de la théorie est celui des caractères des représentations. Le caractère d'une représentation (V, ρ) est la fonction qui à un élément s associe la trace de ρ_s. Un caractère irréductible est le caractère d'une représentation irréductible. Si le corps de l'espace V est de caractéristique première avec g l'ordre du groupe et si le polynôme X^g - 1 est scindé dans le corps, alors les caractères possèdent des propriétés remarquables.

Ce sont des fonctions centrales c’est-à-dire qu'elles sont constantes sur les classes de conjugaison du groupe. De plus, le lemme de Schur permet de démontrer que les caractères irréductibles forment une base orthonormale de l'espace des fonctions centrales.

Ces propriétés permettent simplement de factoriser l'exemple donné sur S₃. L'espace des fonctions centrales est de dimension trois car il existe trois classes de conjugaison différentes. Si φ et ψ sont deux fonctions centrales, c la classe des cycles d'ordre deux et t la classe des transpositions, alors si désigne le conjugué du complexe a, le produit hermitien (l'équivalent du produit scalaire pour les espaces vectoriels complexes) est donné par la formule :

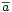
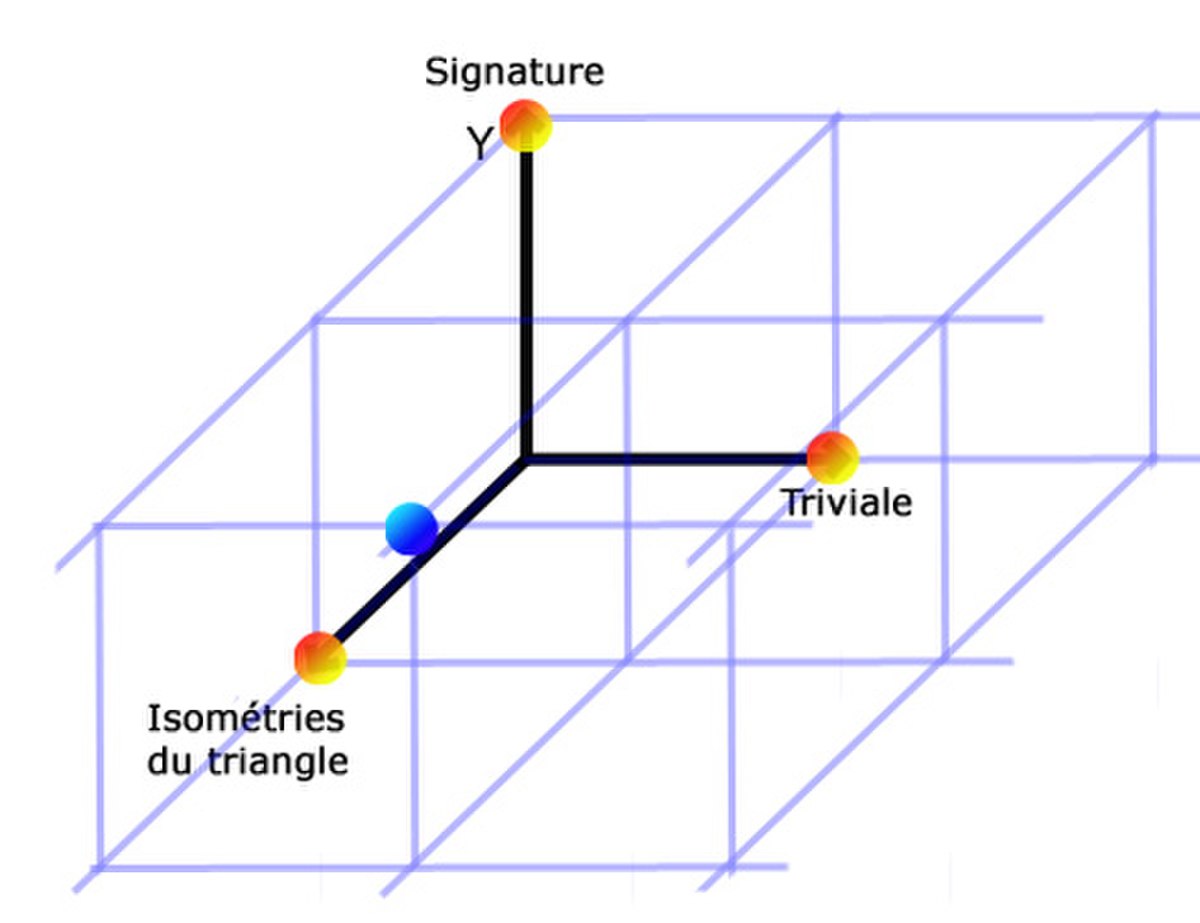
La norme de chacune des trois représentations t, σ et θ est bien égale à un et ils sont orthogonaux deux à deux, ce qui montre qu'ils forment la base des représentations et sont bien les trois représentations irréductibles. Il suffit de calculer le produit hermitien de la représentation de Galois pour déterminer sa factorisation.

La figure de droite illustre le groupe S₃. Les caractères représentés par des boules orange sont les trois irréductibles, la boule bleue représente le caractère de la représentation de Galois. Elle est combinaison linaire des trois caractères irréductibles avec les coefficient un pour la triviale, un pour la signature et deux pour celle des isométries du triangle.

Algèbre du groupe

Joseph Wedderburn

Le deuxième pilier est constitué par l'algèbre du groupe, en général notée K[G]. Le groupe est linéarisé, c’est-à-dire qu'il est identifié à une base d'un K espace vectoriel. Le prolongement de la représentation à la structure forme une algèbre sur un corps :

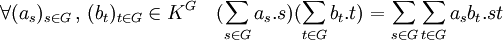
La structure est doublée d'une autre, celle de G-module sur l'anneau K[G]. Elle correspond au prolongement d'une représentation à l'algèbre K[G].

Cette algèbre possède une propriété importante, elle est semi-simple. En conséquence, une théorie algébrique entière, riche en théorèmes permet d'élucider d'autres aspects de la structure. Le plus important est probablement celui d'Artin-Wedderburn. Il indique, dans ce contexte, que l'algèbre est isomorphe à un produit direct d'algèbres connues : les endomorphismes d'un espace vectoriel de dimension finie sur K.

Un exemple est celui du centre de K[G]. Sous l'angle de l'algèbre du groupe, c'est un anneau semi-simple correspondant à un produit de la forme K^h où h est l'entier égal au nombre de sous-algèbres simples. Le centre s'avère être isomorphe aux fonctions centrales du paragraphe précédent. L'isomorphisme est suffisamment naturel pour que les deux structures soit souvent identifiées. Les propriétés d'orthonormalité s'expriment de manières différentes, sources de nombreux théorèmes comme la loi de réciprocité de Frobenius.

Un tel centre ouvre des perspectives nouvelles, c'est un anneau commutatif sur un corps K, il est donc possible d'utiliser les outils de l'arithmétique. Une démarche de cette nature permet par exemple de démontrer que le degré de toute représentation irréductible divise l'ordre du groupe.

Cette algèbre apporte enfin des outils essentiels dans le cas où l'ordre du groupe est un multiple de la caractéristique du corps. La théorie des anneaux, et plus particulièrement celle des idéaux, permet d'élucider la structure.