Résonance paramagnétique électronique - Définition

Principe

Séparation des niveaux d'énergie (pour le cas d'un spin S = 1/2) en présence d'un champ magnétique externe.

La résonance de spin électronique (RSE) est une méthode de spectroscopie sous champ magnétique. Grâce à sa spécificité et sa grande sensibilité, elle permet une détection directe des espèces magnétiques (radicaux, éléments de transition, défauts de structure…) caractérisées par la présence d'un électron non apparié (appelé aussi « électron célibataire ») sur la couche de valence.

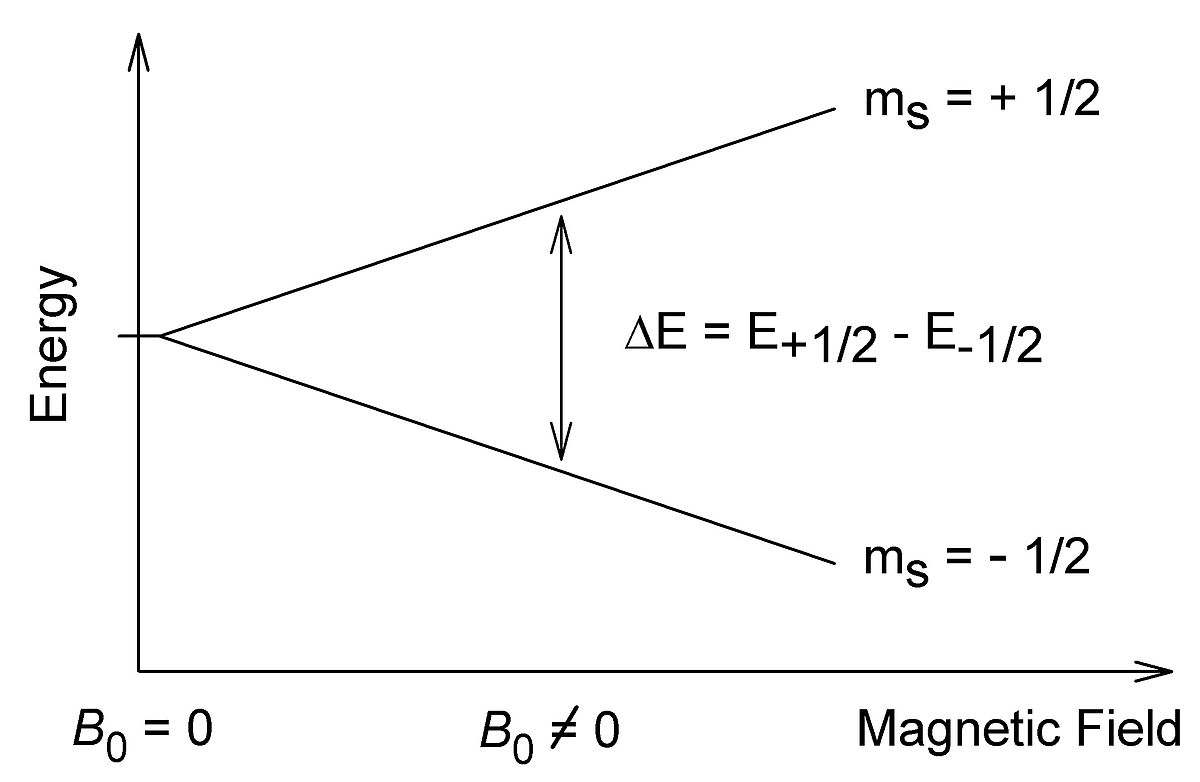
Son principe repose sur l'effet Zeeman : soumis à l'action d'un champ magnétique extérieur intense H, les niveaux d'énergie d'un spin S se séparent en (2S + 1) états, chacun affecté d'un nombre quantique m_S (m_S = -S, -S+1, -S+2, ..., S).

Ainsi, pour le cas d'un ion magnétique ne présentant qu'un seul électron célibataire (donc pour lequel S = 1/2), la présence du champ magnétique extérieur donne lieu à (2S + 1) = 2 états, correspondant à m_S = -1/2 et m_S = +1/2. L'énergie magnétique associée à chacun de ces états est donnée par m_Sgμ_BH, où g est le facteur de Landé lorsqu'il s'agit d'un électron libre mais qui est désigné, dans le cas général, par le facteur g, et μ_B (qui est parfois noté β) est le magnéton de Bohr. Puis, sous l'action d'un second champ magnétique (champ hyperfréquence ou micro-onde) perpendiculaire au premier et d'amplitude beaucoup plus faible, ayant une fréquence ν, un photon d'énergie hν peut être absorbé (ou émis) si la séparation énergétique entre les 2 niveaux concernés, c'est-à-dire gμ_BH, se trouve égale à hν. C'est à cette valeur particulière de H que le phénomène de résonance se produit. Ainsi, la condition de résonance se résume par :

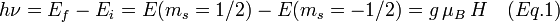
avec

• g = facteur de Landé (dans le cas d'un électron libre) ou facteur g en général ;
• μ_B (ou β) = magnéton de Bohr (μ_B = 9.2741 x 10^-24 J.T^-1) ;
• H = valeur du champ magnétique à la condition de résonance ;
• h = constante de Planck (h = 6.6261 x 10^-34 J.s) ;
• ν = fréquence du champ micro-onde ;
• E _f = énergie de l'état final ;
• E _i = énergie de l'état initial.

D'une façon plus générale, lorsqu'il y a plus que 2 états, les transitions permises sont celles pour lesquelles les états (initial et final) satisfont aux conditions ΔS = 0 et Δm_S = ± 1. Les autres transitions sont généralement interdites, sauf s'il y a un mélange entre les états quantiques.

La condition de résonance exprimée ci-dessus (Éq. 1) peut également s'écrire :

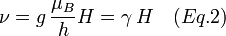
où γ désigne le rapport gyromagnétique.

Spectres typiques d'absorption (courbe du haut) et de la dérivée première de l'absorption (courbe du bas) obtenus à fréquence fixe et en faisant varier le champ magnétique statique externe.

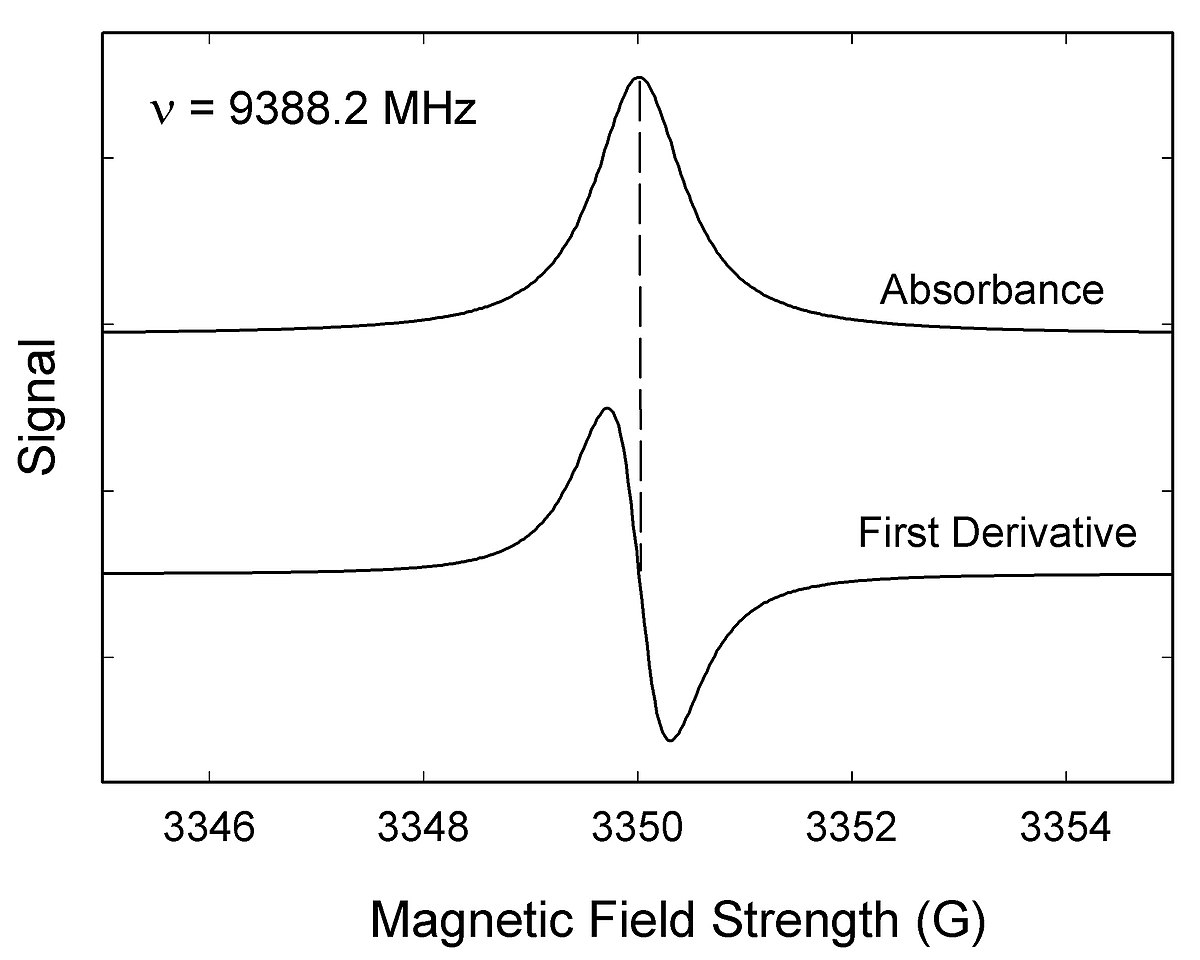
L'équation (Éq. 2) montre qu'il existe une multitude de combinaisons possibles des valeurs de ν et H pour que la résonance ait lieu. En fait, un spectre de résonance de spin électronique peut théoriquement s'obtenir, soit en fixant le champ magnétique statique H et en faisant varier la fréquence ν du champ micro-onde, soit en faisant l'inverse. Cependant, en pratique, la plupart des spectromètres fonctionnent en permettant la variation du champ magnétique H alors que la fréquence ν est fixée.

La figure ci-contre montre, dans sa partie supérieure, la variation de l'absorption, A, en fonction du champ magnétique statique H, lorsque la fréquence fixe utilisée est de 9388,2 MHz. La courbe inférieure représente la dérivée première de l'absorption par rapport au champ magnétique, dA/dH. La plupart des spectromètres de RSE utilisent un détection synchrone, c'est-à-dire que le champ magnétique est modulé autour d'une valeur centrale telle que

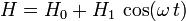
Le signal d'absorption peut s'écrire à l'ordre 1 sous la forme :

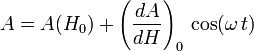
En filtrant la fréquence correspondant à ω on obtient dA/dH, la courbe dérivée.

Chaque signal ainsi enregistré est caractéristique de l'élément magnétique en présence et des interactions que cet élément ressent. Ces informations s'obtiennent à partir de (i) la valeur du champ de résonance (qui informe sur le facteur g de l'ion magnétique en question), (ii) l'aire en dessous de la courbe d'absorption (qui informe, entre autres, sur le nombre de spins présents) et (iii) la mi-largeur à mi-hauteur de la courbe d'absorption (qui informe sur les interactions ressenties par les spins). Le nombre de signaux indique parfois le nombre de site ou bien des interactions avec un (ou plusieurs) spins nucléaires. Si tel est le cas, on peut réaliser alors un spectre de résonance magnétique nucléaire détectée par RSE, l'ENDOR.