Système de numération - Définition

Systèmes de notation

On distingue schématiquement trois familles de systèmes de notation.

• Les systèmes additifs utilisent des symboles pour représenter certains nombres, les autres nombres s'obtenant par juxtaposition de ces symboles. Le lecteur a alors la charge d'additionner les valeurs de chaque symbole pour retrouver la valeur du nombre. C'est le cas des systèmes de numération grec, égyptien, gotique, ou plus simplement du système unaire ou de la numération forestière. C'est aussi le cas avec une variante soustractive pour le système de numération romain.
• Les systèmes hybrides utilisent des symboles différents pour les puissances de la base et pour les nombres inférieurs à la base écrits devant le symbole. Les nombres sont ainsi représentés par addition de multiples de puissances de la base. C'est le cas des systèmes de numération chinois et japonais. On peut remarquer qu'un tel système de notation comporte une forte analogie avec le système d'énonciation des nombres dans une majorité de langues. (Par exemple, en français, le nombre deux-mille-huit-cent-dix-sept, est aussi formé par addition de multiples de puissances de la base 10 : 2×10³+8×10²+1×10¹+7.)
• Les systèmes positionnels utilisent un symbole à chaque position, la place du symbole dans l'écriture du nombre indiquant le poids qui lui est affecté (poids n⁰=1, poids n¹=n, poids n², … pour une base n). C'est le cas des systèmes de numération maya et babylonien, ainsi que les systèmes de numération indien et arabe, qui sont à l'origine des mathématiques modernes, celles-ci permettant désormais d'écrire les nombres simplement quelle qu'en soit la base, à l'aide du zéro positionnel.

Systèmes de mime

Les peuples se servent traditionnellement des parties de leur corps pour compter. Pour un compte décimal ou quinaire, les doigts sont généralement mis à contribution. Les Yukis, qui emploient un système octal, utilisent des espaces entre les doigts pour compter. Le peuple chepang, qui emploie un système duodécimal, se sert du pouce pour compter sur les phalanges des doigts. Bien d'autres procédés encore ont été employés.

Système de numération en mathématiques

Définition

Un système de numération est un triplet (X , I , ϕ), où X est l'ensemble à énumérer, I est un ensemble fini ou dénombrable de chiffres et ϕ est une application injective dans les suites de chiffres , .

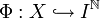
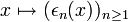
En notation décimale, X est l'ensemble des entiers naturels, est l'ensemble des chiffres décimaux et la suite associée à un nombre entier est la suite de ses chiffres décimaux.

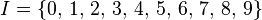
L’application ϕ est appelée application de représentation, et ϕ(x) est la représentation de x∈X.

Les suites admissibles sont définies comme les représentations images ϕ(x), pour x∈X.

Exemples

• La représentation q-adique, ou écriture en base q: tout entier naturel s'écrit de manière unique comme , avec les chiffres et où est le nombre de chiffres de n en base q. De même, tout réel peut s'écrire, de manière unique si son développement est propre (pas de suite infinie de q-1 comme 0,999...=1), comme .
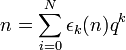
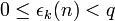
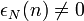
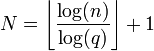
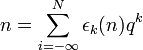
• La représentation de Zeckendorf: Les nombres de Fibonacci F₀ = 1, F₁ = 2, F_{n + 2} = F_{n + 1} + F_n permettent d'écrire tout entier naturel de manière unique comme , avec les chiffres et .
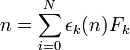
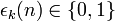
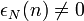
• La représentation en fractions continues: Tout nombre réel peut s'écrire (de manière unique si le développement est propre) avec et pour k>0.
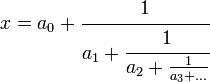
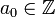
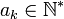
• La β-numération où β est une base non entière, la base d'or en est un exemple.
• La décomposition en nombres premiers est un système de numération, .

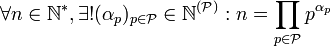
• Le système modulaire de représentation (RNS) permet, à l'aide d'une base de modules mutuellement premiers entre eux, d'énumérer tous les nombres entiers jusqu'à par leur suite de restes en utilisant le théorème des restes chinois.

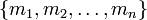
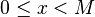
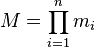
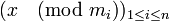
Système de numération fibré

Les chiffres proviennent d'une transformation non injective

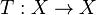
• En représentation q-adique, le "chiffre des unités" est donné par et la suite des chiffres par ε_k(n) = ε(T^k(n)) où T est l'application T(n) = (n − ε(n)) / q.
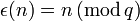
• La suite des chiffres de la représentation en fractions continues provient de et l'application de Gauss T(x) = 1 / x − ε(x).