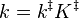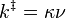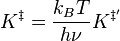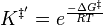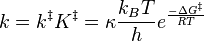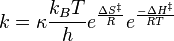Théorie de l'état de transition - Définition

Introduction

Figure 1 : diagramme de réaction pour une réaction de substitution nucléophile bimoléculaire (S_N2) entre le bromométhane et l'anion hydroxyde

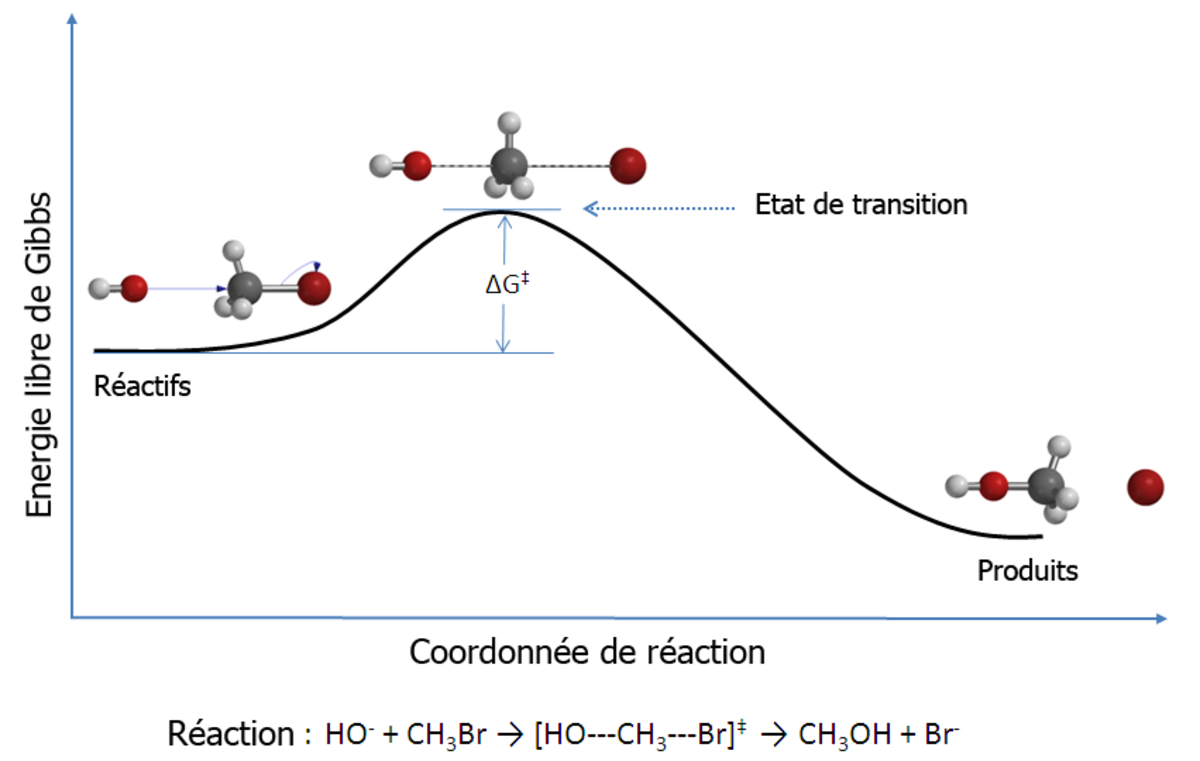
La théorie de l'état de transition (en anglais transition state theory - TST) a pour objectif d'expliquer les cinétiques de réaction pour des réactions chimiques élémentaires. Cette théorie postule l'existence d'un genre spécial d'équilibre chimique, le quasi-équilibre, entre les réactifs et un complexe de transition activé.

La TST est utilisée en premier lieu pour comprendre de manière qualitative le déroulement des réactions chimiques. La théorie a connu moins de succès dans son but initial de calculer des constantes cinétiques absolues pour les réactions, ces calculs nécessitant la connaissance précise des surfaces d'énergies potentielles, mais permet de calculer efficacement l'enthalpie standard d'activation (Δ^‡H°), l'entropie standard d'activation (Δ^‡S°), et l'énergie standard d'activation de Gibbs (Δ^‡G°) pour une réaction donnée si sa constante cinétique a été déterminée expérimentalement (la notation ^‡ indique que la constante cherchée est à l'état de transition).

Cette théorie a été développée simultanément en 1935 par Henry Eyring, à Princeton, et par Meredith Gwynne Evans et Michael Polanyi à l'Université de Manchester.

La théorie de l'état de transition est aussi connue sous les noms de théorie du complexe activé, théorie de la cinétique absolue ou théorie des cinétiques de réaction absolues.

Avant le développement de la TST, la loi cinétique d'Arrhenius était largement utilisée afin de déterminer les énergies des barrières de réactions. La loi d'Arrhenius est déduite d'observations empiriques et ne prend pas en compte de considérations mécanistiques, comme par exemple de savoir si un ou plusieurs réactifs intermédiaires sont impliqués dans le passage d'un réactif à un produit. Cependant, un développement plus poussé était nécessaire afin de comprendre les deux paramètres associés à cette loi, le facteur pré-exponentiel (A) et l'énergie d'activation (E_a). La TST, qui conduit à l'équation d'Eyring, permet de déterminer ces deux paramètres ; cependant, 46 ans se sont écoulés entre la publication de la loi cinétique d'Arrhenius en 1889 et celle de l'équation d'Eyring dérivée de la TST en 1935. Durant cette période, de nombreux scientifiques et chercheurs ont contribué de manière significative au développement de la théorie.

Théorie

Les idées de base sur lesquelles s'appuie la théorie de l'état de transition sont les suivantes :

1. les cinétiques des réactions sont étudiées par le biais des complexes activés qui se situent aux cols (points-selles) d'une surface d'énergie potentielle. Les détails de la formation de tels complexes importent peu.
2. les complexes activés sont en équilibre spécial (quasi-équilibre) avec les molécules réactives.
3. les complexes activés peuvent évoluer en produits, ce qui permet à la théorie cinétique de calculer la cinétique de cette conversion.

Origine de l'équation d'Eyring

Le point crucial ajouté par Eyring, Polanyi et Evans est que les complexes activés sont en quasi-équilibre avec les réactifs. La constante cinétique est directement proportionnelle à la concentration de ces complexes multipliée par la fréquence (k_BT/h) de leur conversion en produits de réaction.

Approximation de l'état quasi-stationnaire

Il est important de souligner que ce quasi-équilibre est différent de l'équilibre chimique classique, mais qu'il peut être décrit en utilisant le même traitement thermodynamique. Soit la réaction :

Figure 2 : diagramme d'énergie potentielle.

où l'équilibre est atteint entre toutes les espèces du système, y compris les complexes activés, [AB]^‡. En utilisant la mécanique statistique, la concentration de [AB]^‡ peut être calculée en fonction des concentrations de A et B.

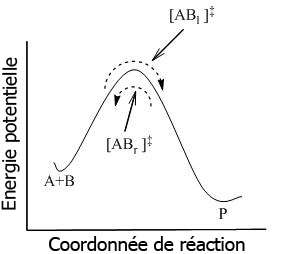
La TST postule que même lorsque les réactifs et les produits ne sont pas en équilibre entre eux, les complexes activés sont en quasi-équilibre avec les réactifs. Comme indiqué figure 2, à tout instant, il existe quelques complexes activés, certains étant des réactifs dans l'instant précédent, étant désignés par [AB_l]^‡ (lorsqu'ils sont déplacés de gauche à droite). Le reste d'entre eux étaient des produits dans l'instant précédant, [AB_r]^‡. Lorsque le système est en équilibre complet, les concentrations en [AB_l] ^‡ et [AB_r]^‡ sont égales, donc chaque concentration est égale à la moitié de la concentration totale en complexes activés :

et

Si les molécules produit sont subitement retirées du système réactionnel, le flux des complexes activés provenant des produits ([AB_r]^‡ ) sera interrompu ; cependant, il existera toujours un flux provenant des réactifs. Ainsi, le postulat est que la cinétique du flux de la gauche vers la droite n'est pas influencé par le retrait des produits. En d'autres termes, les flux dans les deux directions sont indépendants l'un de l'autre.

Dans le cadre de la TST, il est important de comprendre que lorsque des complexes activés sont dits en équilibre avec les réactifs, on considère seulement les complexes activés ([AB_l] ^‡) qui étaient des réactifs dans l'instant immédiat.

La constante d'équilibre K^‡o pour le quasi-équilibre peut être écrite :

La concentration de l'état de transition AB^‡ est donc :

L'équation cinétique de production du produit est alors :

Où la constante cinétique est donnée par :

k^‡ est directement proportionnelle à la fréquence du mode de vibration responsable de la conversion du complexe activé en produit ; ce mode a pour fréquence ν. Chaque vibration ne conduit pas forcément à la formation d'un produit. Une constant proportionnelle κ, appelée coefficient de transmission, est donc introduite pour prendre en compte cet effet. k^‡ peut alors être réécrite :

Pour la constante d'équilibre K^‡ , la mécanique statistique conduit à une expression dépendante de la température donnée par :

où

En combinant les nouvelles expressions pour k^‡ et K^‡,une nouvelle expression de la constante cinétique peut être écrite, donnée par :

Puisque ΔG = ΔH –TΔS, la constante cinétique peut être développée en ce qui est appelé l'équation d'Eyring :

L'expression de la constante cinétique TST peut être utilisée afin de calculer ΔG°^‡, ΔH°^‡, ΔS°^‡ et parfois ΔV^‡ (le volume d'activation) en utilisant les données cinétiques expérimentales.