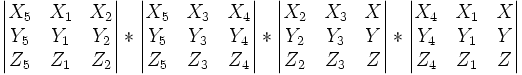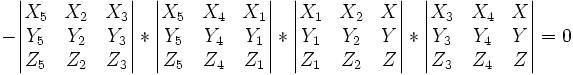Traité projectif des coniques/Dans un plan pappusien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La géométrie est l'art de raisonner juste sur des figures fausses. ( auteur à retrouver )
- Dans un plan arguésien on ne peut pas définir le concept de conique, seulement le concept de bi-ensemble de points dont tous les hexagrammes alternés sont pascaliens. Maintenant, si on s'octroie le droit d'utiliser l'axiome de Pappus, tout se simplifie, les coniques existent, la tangente en un point aussi, les polaires aussi.
Anticipation: hexagone de Brianchon et hexagramme de Pascal
<-----Retour au traité projectif des coniques
Plan projectif arguésien et absence des coniques.
- voir <------Retour au traité projectif des coniques
- Résumé. Dans un plan projectif arguésien les coniques n'existent pas. On peut y seulement faire 6 permutations (sur 60) d'un hexagramme pascalien.
Ce que l'on sait de l'approche de Pascal lui-même.
(voir Traité projectif des coniques, §Ce que l'on sait de l'approche de Pascal lui-même/ boîte déroulante)
Plan projectif pappusien et coniques.
La première démarche sera de montrer que toute permutation d'un Hexagramme de Pascal conserve la propriété de pascalinité. Puis toutes les conséquences viennent assez facilement (tangente en un point, intersection avec une droite, polaires). La définition d'une conique en termes d'Hexagramme de Pascal est proche de celles par la constance du rapport anharmonique, par les équations du second degré, par la transformation homographique d'un faisceau de droites.
Lorsque nous lisons actuellement des manuels de géométrie projective d'un formalisme absolu, sans figure, nous pensons que les étudiants ne peuvent, faute de formation adéquate, en comprendre la substance-Anne Boyé, Pour la science n°21, novembre 2004-février 2005.
Substitution de deux voisins.
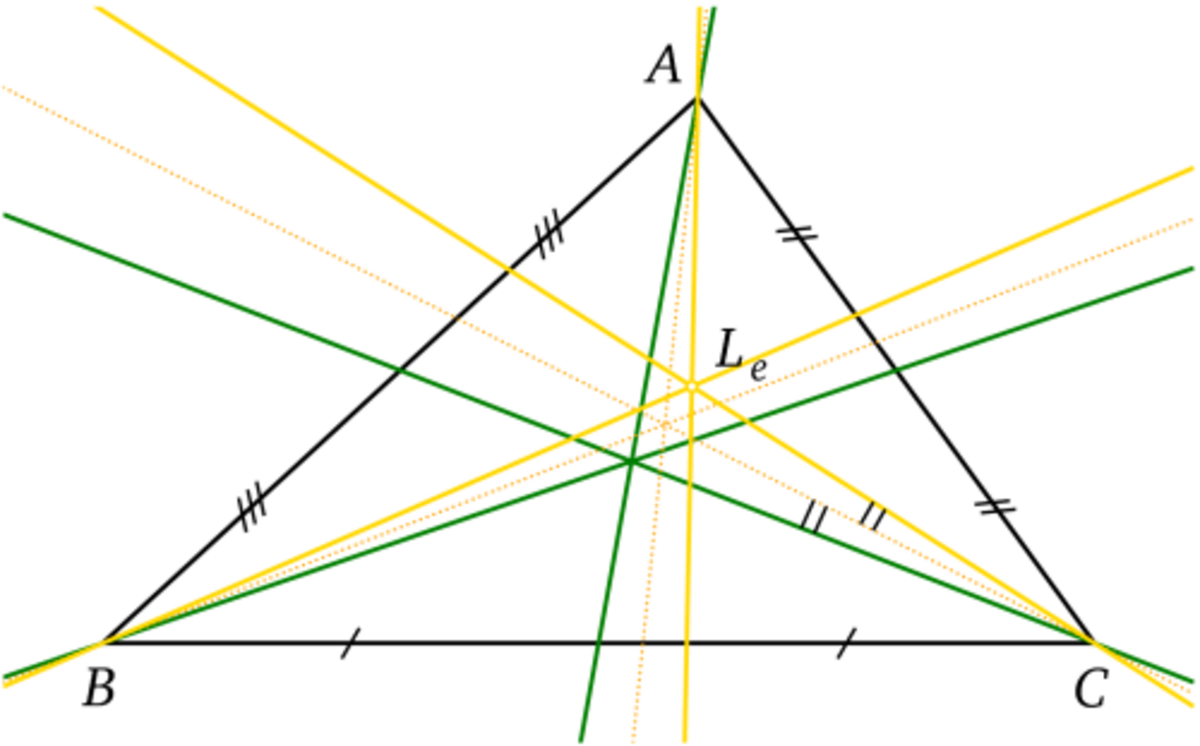
Le théorème principal est : Dans un plan projectif pappusien, si un hexagramme est pascalien, alors l'hexagramme obtenu en substituant deux points voisins est lui aussi pascalien. Sur la figure ci-contre la conique est simplement évoquée en forme de "patatoïde", on ne travaille que sur 6 de ses points, on échange les points P3 et P4 pour étudier l'hexangle ordonné P1 P2 P4 P3 P5 P6 P1.
La substitution concerne les deux points voisins P3 et P4.
- La démonstration est simple. Nous sommes dans un plan pappusien, considérons les deux alignements B-4-5 et C-2-3. Ils permettent de créer l'hexagramme pappusien BC5342B. Les trois couples de droites BC-34, C5-42 et 53-2B se coupent en trois points A, Y et Z qui sont donc alignés. CQFD.
En d’autres termes si le plan est pappusien et si le produit
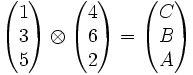
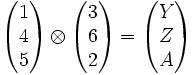
- Bien entendu, une fois démontrée l'invariance de la propriété à une substitution de 2 voisins, compte tenu de l'invariance de la propriété à la permutation circulaire des 6 points, on peut engendrer les 60 permutations de l'hexagramme et en déduire que la propriété est vraie pour tous. En d'autres termes, Dans un plan projectif pappusien, si un hexagramme ordonné est pascalien, alors les 59 autres hexagrammes ordonnés le sont.
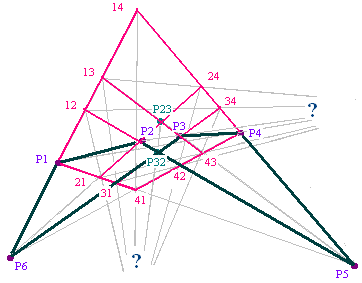
Un quadrillage complet dans un plan projectif pappusien.
La figure de l'hexagramme pascalien dans laquelle on distingue 2 points (P5 et P6)que l'on relie aux quatre autres points forme un quadrillage 4x4 qui ne manque pas de rappeler un sol carrelé de certaines peintures de la renaissance mais qui serait vu en biais. :
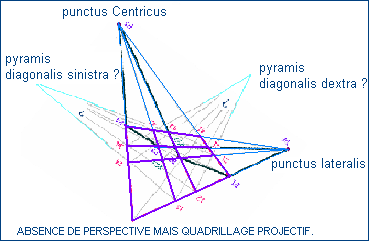
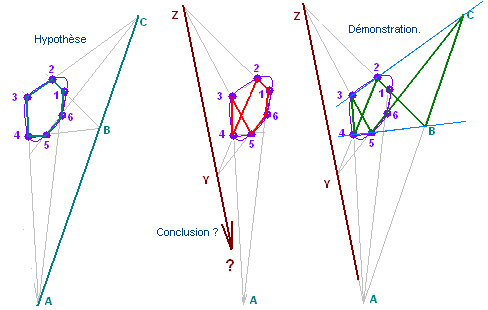
- Dans cette figure, il y a un hexagramme ordonné : P5-1-2-6-4-3-5. De deux choses l'une, soit il n'est pas pascalien, soit il l'est. S'il l'est, que peut-on dire de diverses droites diagonales du quadrillage,
Hypothèse : l’hexagramme est pascalien. Donc les trois points P32, 14, Z sont alignés. Une application du théorème dual de Désargues aux triangles 1-2-12 et 4-3-34 mène à la convergence des trois diagonales 1-4 , 2-3 et 13-34 en un point que nous appelerons U.
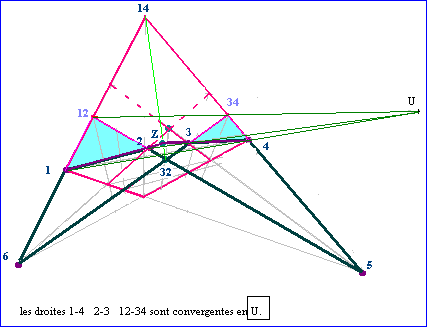
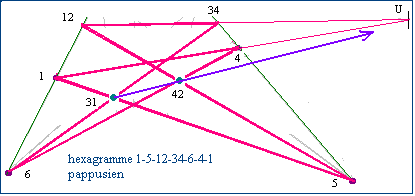
- L'application de l'axiome de Pappus à l'hexagramme 1-5-12-34-6-4-1 montre que la diagonale 31-42 passe aussi par U.
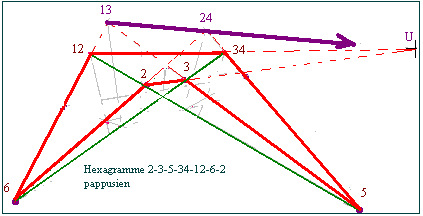
- L'application de l'axiome de Pappus à l'hexagramme 2-3-5-34-12-6-2 montre que la diagonale 13-24 passe aussi par U.
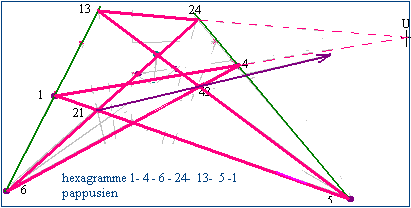
- L'application de l'axiome de Pappus à l'hexagramme 1-4-6-24-13-5-1 montre que la diagonale 21-43 passe aussi par U. A ce stade nous avons mis en évidence six diagonales qui ont un point commun U.
- L'application du théorème de Désargues aus triangles (vus en perspective depuis U) 1-13-31 et 4-24-42 montre que les trois diagonales 13-31, 14-41 et 24-42 convergent en un point que nous appellerons V.
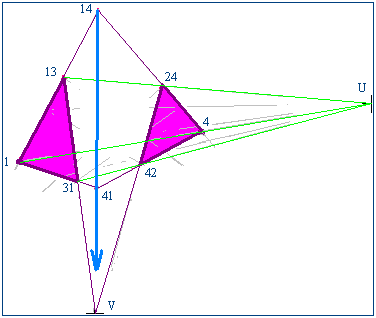
- L'application de l'axiome de Pappus à l'hexagramme 5-13-31-6-41-14-5 montre que la diagonale 34-43 passe aussi par v.
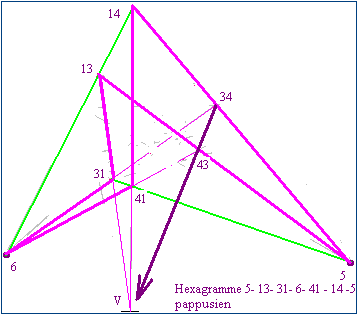
- D'autres applications du théorème de Pappus achèveront la démonstration avec les diagonales 23-32 et 34-43. Ainsi, si l'hexagramme 1-2-5-4-3-6-1 est pascalien, alors il y a 6 diagonales passant par U et 6 diagonales passant par V.
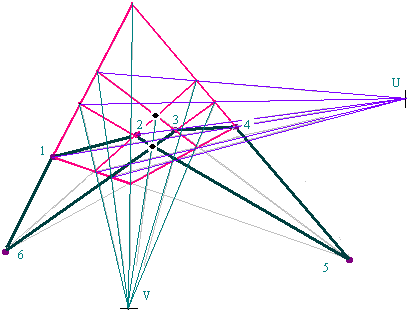
Existe-t-il une tangente dans un plan projectif pappusien?
Intersection droite/conique dans un plan projectif pappusien.
Polaire dans un plan projectif pappusien.
Hexagrammes mystiques en géométrie euclidienne.
Un cas concerne le cercle d'Euler, ou de Feuerbach, cas particulier de conique à propos de laquelle on peut démontrer que la droite d'Euler est la droite de Pascal de l'hexagramme mystique H1-I2-H3-I1-H2-I3-H1.
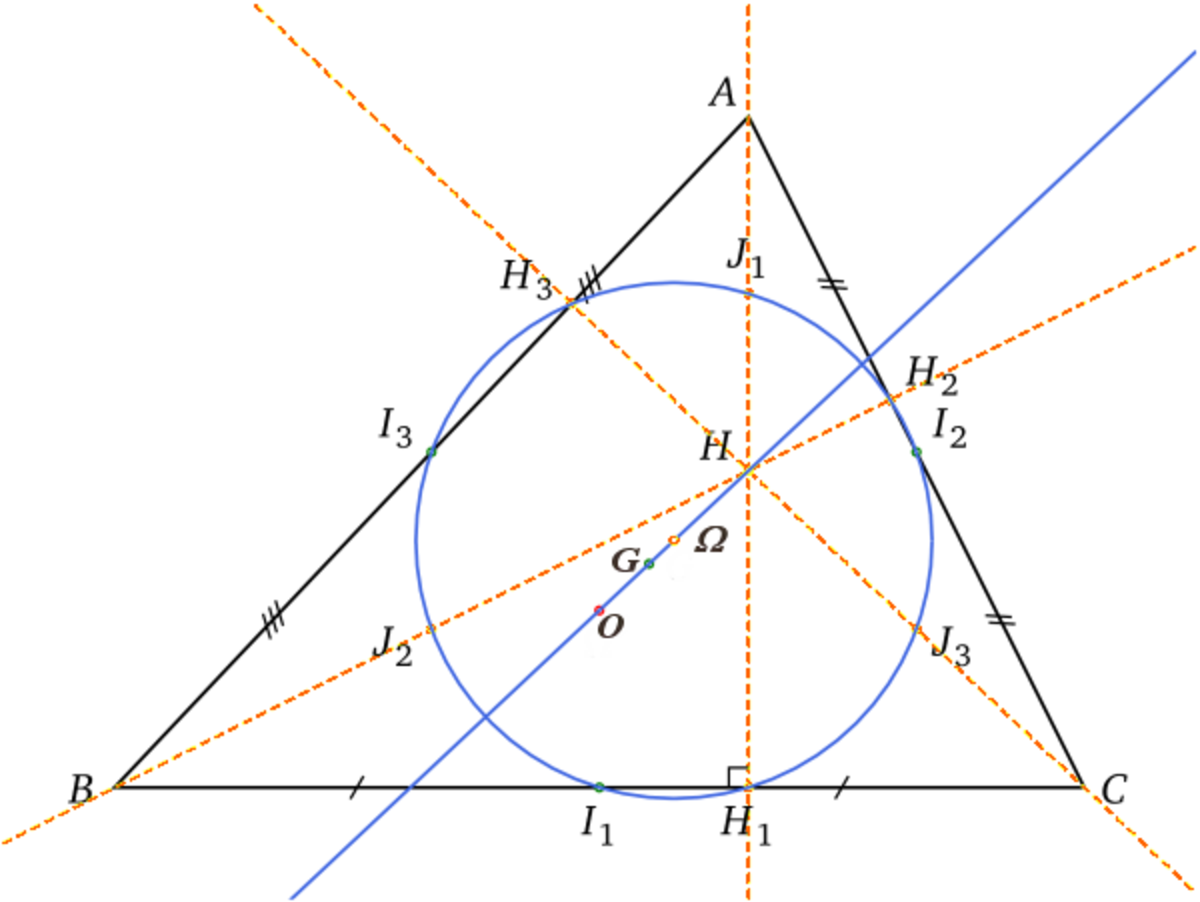
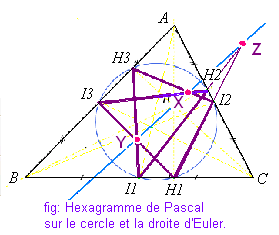
- Dans le même esprit il est intéressant d'examiner les propriétés relatives des 2 trigones (ABC) et H1I2, H2I3, H3I1: sont-ils en perspective arguésienne?
- On peut se poser le même genre de questions à propos du point de Lemoine et de la conique éventuelle qui passerait par les 6 pieds des céviennes concernées.
- D'une manière plus générale on peut considérer 6 points: les pieds des céviennes d'un point P et les pieds des céviennes de son conjugué isogonal Q; réf biblio par exemple La géométrie du triangle, Yvonne et René Sortais, Hermann, 1997, chapitres à partir de "isogonalité".
Hexagramme et définitions traditionnelles d'une conique.
Si, dans un plan projectif pappusien, nous pouvons définir le concept de conique grâce à l'hexagramme pascalien, il faut voir si ce concept correspond avec les définitions traditionnelles des coniques.
Lien avec les rapports anharmoniques.
A partir d'un hexagramme pascalien, peut-on inférer qu'il y a conservation du rapport anharmonique sur une conique? La réponse est oui si le plan est pappusien. La démonstration se fait sur la figure du quadrillage complet vue précédemment.
- Nous avons donc établi l'égalité de deux birapports de faisceaux
- ((P5-P1),(P5-P2),(P5-P3), (P5-P4)) = ((P6-P1),(P6-P2),(P6-P3), (P6-P4))
- On en déduit que, connaissant 5 points P1 ,2 3 4 5, on décrit la conique en faisanr bouger le sixième point à rapport anharmonique constant.
Lien avec le second degré.
On peut établir d'abord ce lien en coordonnées homogènes, puis passer aux coordonnées cartésiennes. Les petites astuces de calcul méritent des explications d'algèbre linéaire. En coordonnées homogènes nous écrirons l'égalité des faisceaux anharmoniques, la conique étant définie par 5 points fixes, le sixième étant mobile. Un rapport anharmonique s'exprime avec 4 produits de matrices (matriceligne * matricecolonne) ou un produit scalaire si on préfère; une matrice-ligne représente une droite du faisceau, droite qui est en fait définie par un point de départ et un point d'arrivée. En coordonnées homogènes ceci se traduit par un "produit vectoriel". Si on enchaîne les deux opérations, on a donc (un produit vectoriel) multiplié scalairement par (un vecteur-colonne), ce qui revient à faire le déterminant des 3 vecteurs en question, mis en colonne. Notre égalité de rapports anharmoniques sera composée d'une équation entre 8 déterminants 3x3.
- Dans une conique qui contient les 6 points P1, 2, 3, 4, 5, 6 (et donc les cordes d51, d52, d53 etc) le rapport anharmonique des points 1, 2, 3, 4 vus du point 5 peut être exprimé par
-
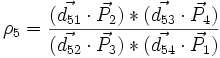
-
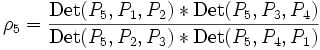
- De la même manière le rapport anharmonique des mêmes points 1, 2, 3, 4 vus du point peut être exprimé par
-
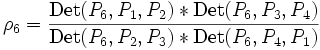
- Ecrire que ces deux birapports sont égaux revient à écrire
- Det(P5,P1,P2) * Det(P5,P3,P4) * Det(P6,P2,P3) * Det(P6,P4,P1) = Det(P6,P1,P2) * Det(P6,P3,P4) * Det(P5,P2,P3) * Det(P5,P4,P1)
- En explicitant les coordonnées homogènes des 6 points, l'équation d'égalité des deux rapports anharmoniques est
-
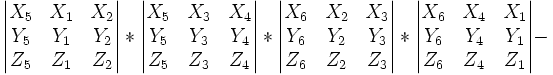
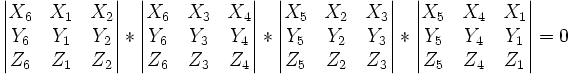
. Si les 5 premiers points sont fixes et le 6ème mobile de coordonnées variables X, Y, Z au lieu de X6, Y6, Z6, on obtient une équation homogène du second degré, donc une conique est une courbe du second degré que l'on peut développer et transformer si on le souhaite.
Lien avec la définition monofocale
La définition monofocale des coniques, encore appelée définition par foyer et directrice (voir Conique), peut ^tre déduite par calculs de la définition analytique du deuxième degré ci-dessus.
Lien avec les faisceaux homographiques
Des exemples peuvent être trouvés dans les pages:
| constructions ponctuelles | constructions tangentielles |
|---|---|
| ************************************************************** | ************************************************************** |
| Construction d'un cercle point par point | pour présenter des données chiffrées |
| Construction point par point | Construction d'une parabole tangente par tangente |
La démonstration se fait sur la figure du quadrillage complet vue précédemment. Si l'hexagramme 1254361 est pascalien, alors les diagonales 12-21, 13-31 et 14-41 convergent en un point V figuré ici par le point d'interrogation.

- Le faisceau de départ est de centre P5,
- il est coupé par la droite P6-P14
- à partir de ces intersections on définit un faisceau homographique de centre V,
- qui à son tour est coupé par la droite P5-P14
- à partir de ces intersections on définit le faisceau d'arrivée de centre P6 qui lui est homographique.
- l'intersection d'une droite du faisceau P5 de départ et de son homographique du faisceau P6 d'arrivée engendre une conique.
- Remarque. En toute rigueur axiomatique pour démontrer cette propriété on a aussi besoin d'être dans un Plan projectif fondamental, qui nous assurera que la définition précédente de la transformation unidimensionnelle entre les faisceaus P5 et P6 est bien une homographie parfaitement définie par les 5 points P1,2,3,6,5, le point 4 étant l'intersection variable d'une droite du faisceau P5 de départ et de son homographique du faisceau P6.